数字基带信号的频谱分析特性

在研究了数字基带信号的时域波形之后,还需要对数字基带信号的频域特性进行分析,这样才能够对数字基带信号有一个全面的认识。

通常数字信号是一串随机的脉冲序列,而随机信号不能用确定的时间函数表示,因此它没有确定的频谱函数,只能用功率谱密度描述其频率特性。根据随机信号分析理论,若求功率谱表达式,应先求出随机序列的自相关函数,这样的方法相当复杂。较简单的方法是由随机过程功率谱的原始定义出发,求出简单码型的功率谱密度。

设一个二进制的随机脉冲序列如图5.3.1所示。其中,用g1(t)和g2(t)分别表示符号的0和1,码元宽度为Ts。虽然图中将g1(t)和g2(t)都画成高度不同的三角形,但实际上g1(t)和g2(t)表示的是任意脉冲。

图5.3.1　任一随机脉冲序列波形

设前后码元统计独立,且g1(t)出现的概率为P,则g2(t)出现的概率为1-P,该序列s(t)可以写成

其中,

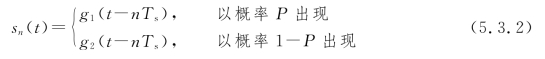
由随机信号分析理论可知,s(t)的功率谱密度函数为

截取时间为

式中,N为一个足够大的数值。且

于是式(5.3.3)变为

截短信号sT(t)可以表示成两部分的和,即

式中,vT(t)为随机信号sT(t)的平均分量,即稳态波;uT(t)为随机信号sT(t)的交变分量,即交变波。稳态波vT(t)是周期性的,是sT(t)的数学期望,即

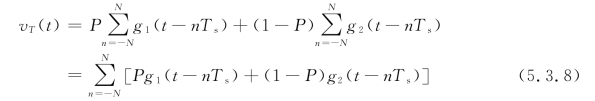
当T→∞时,vT(t)变成v(t)为

由于v(t+Ts)=v(t),即v(t)是以为周期的周期信号,可将其展开成傅里叶级数为

式中,Vm是指数形式傅里叶级数的系数,利用g1(t)和g2(t)的傅里叶变换G1(f)和G2(f),即

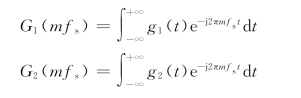
可得出Vm为

由周期性信号的功率谱公式可求得v(t)的功率谱为

交变分量是

可以将uT(t)表示成

其中,

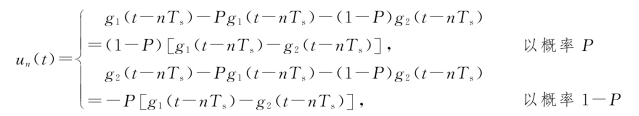
此式可以简写为

这里的{an}为交变分量的随机幅度序列,即

uT(t)的频谱函数UT(f)为

(www.xing528.com)

式中,

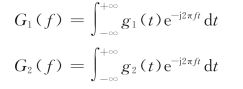
可得出uT(t)能量谱的统计平均值为

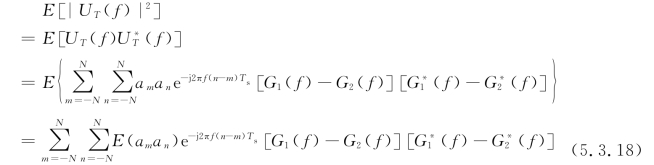
由式(5.3.16)可知{an}具有这样的性质:

当m≠n时,

则

当m=n时,

则

可以将式(5.3.21)和式(5.3.23)综合表示为

将式(5.3.24)代入式(5.3.18),当m=n时,有

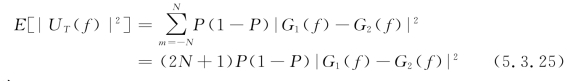
则u(t)的功率谱为

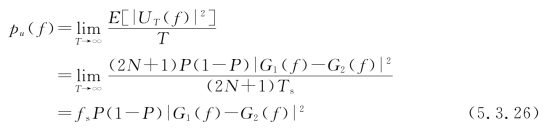
s(t)的功率谱ps(f)是pu(f)与pv(f)的和,由式(5.3.12)和式(5.3.26)可以求出

当波形为单极性时,设g1(t)=0、g2(t)=g(t),则随机脉冲序列的功率谱密度函数为

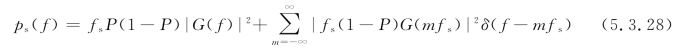
式中,G(f)是g(t)的频谱函数。

此时,如果且g(t)为矩形脉冲,即有

则式(5.3.28)变为

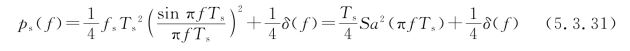
当波形为双极性时,设g1(t)=-g2(t)=g(t),则有

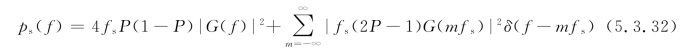
当时,式(5.3.32)变为

如果g(t)为矩形脉冲,则有

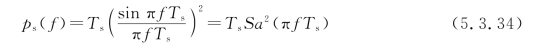
由式(5.3.27)可以看出,二进制随机脉冲序列的功率谱可能包含连续谱和离散谱两部分。连续谱是由于g1(t)和g2(t)不完全相同,使得G1(f)≠G2(f)而形成的,所以它总是存在的。离散谱则由于它与g1(t)和g2(t)的波形及出现的概率均有关系而不一定存在。另一方面离散谱的存在与否直接关系到能否从脉冲序列中直接提取位定时信号,因此离散谱的存在是非常重要的。如果不能保证离散谱的存在,就要通过变换基带信号的波形来满足提取定时信号的需要。

通过以上分析可以得出以下几个结论:

(1)数字基带信号功率谱的形状取决于单个波形的频谱函数,而码型规则仅起到加权作用,使功率谱形状有所变化。

(2)时域波形的占空比愈小,频带愈宽。一般用谱零点带宽Bs作为矩形信号的近似带宽。

(3)凡是0、1等概率的双极性码均无离散谱,即这类码型无直流分量和位定时分量。

(4)单极性归零码的离散谱中有位定时分量。对于那些不含有位定时分量的码型,可以将其变换成单极性归零码,便可获取位定时分量。其变换方法很简单。