角度调制的基本概念与应用实践

线性调制是通过调制信号改变余弦载波的幅度参数来实现调制的,而非线性调制是通过调制信号改变余弦载波的角度(频率或相位)来实现的。

任何一个余弦载波,当它的幅度保持不变时,可用下式表示:

式中,θ(t)称为余弦载波的瞬时相位。如果对瞬时相位θ(t)进行求导,可得到载波的瞬时角频率ω(t),即

ω(t)与θ(t)的关系可用下式表示:

1.角度调制的一般表示式

角度调制的波形一般可以写成

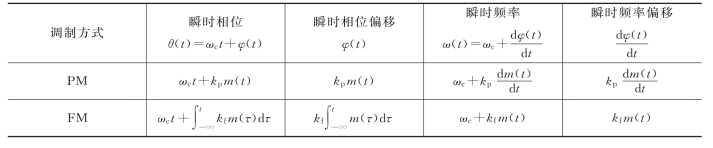
式中,A0为已调载波的振幅;ωct+φ(t)称为信号的瞬时相位,d[ωct+φ(t)]/dt=ωc+称为瞬时角频率(也称为瞬时频率);φ(t)称为瞬时相位偏移(简称瞬时相偏),ω(t)-ωc称为瞬时频率偏移(简称瞬时频偏)。

2.调相波的概念

所谓相位调制,是指载波的振幅不变,载波的瞬时相位随着基带调制信号的大小而变化,实际上是载波瞬时相位偏移与调制信号成比例变化。反过来说,相位调制是由调制信号m(t)去控制载波的相位而实现其调制的一种方法。

由于载波瞬时相位偏移与调制信号成比例的变化,因此令φ(t)=kpm(t),其中kp为比例常数(常称为调相灵敏度)。所以,调相波的表示式为

式中,ωct+kp·m(t)是PM信号的瞬时相位;kp·m(t)是瞬时相位偏移是瞬时频率是瞬时频率偏移(瞬时频偏);最大相位偏移为

最大频率偏移为

3.调频波的概念

所谓频率调制,是指载波的振幅不变,用调制信号m(t)去控制载波的瞬时频率偏移来实现其调制的一种方法。已调信号的瞬时频率随着调制信号的大小变化,实际上是载波的瞬时频率偏移与调制信号成比例变化。因此设

式中,kf为比例常数,单位为rad/(s·V),称为调频器的灵敏度。对kfm(t)进行积分,有

式中,是初始相位,一般认为它等于零。调频波的表示式为FM信号的瞬时相位是;瞬时频率是ωc+kfm(t);瞬时相位偏移为;瞬时频率偏移为kfm(t);最大频偏为|kfm(t)|max;最大相偏为

例4.4.1 已知单音调制信号为m(t)=Acosωmt,试求此时的调相波和调频波,并进行讨论。

解 已知调制信号的表达式,可将其直接代入到PM和FM信号的公式中,得到PM波形和FM波形。

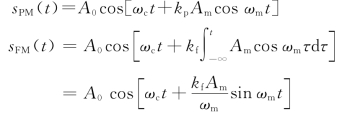
在PM表达式中,瞬时相位为ωct+kpAmcosωmt;瞬时相偏为kpAmcosωmt;最大相偏为kpAm;瞬时频率为ωc-kpAmωmsinωmt;瞬时频偏为kpAmωmsinωmt;最大频偏为kpAmωm。

在FM表达式中,瞬时相位为;瞬时相偏为最大相偏为;瞬时频率为ωc+kfAmcosωmt;瞬时频偏为kfAmcosωmt;最大频偏为kfAm。

为了便于比较,下面把一般PM和FM信号的瞬时相位、瞬时频率、相位偏移、频率偏移归纳如表4.4.1所示。

表4.4.1　PM和FM信号的几个概念

PM信号和FM信号的波形一般不容易画出,只有当调制信号是一些特殊波形时才能画出。图4.4.1画出了基带调制信号是三角波、正弦波、双极性矩形脉冲时的AM、FM和PM波形示意图。

从图4.4.1中可以看到:

①PM与FM信号的幅度恒定不变。

②调制信号m(t)的大小反映在FM信号与时间轴交点(即零点)的疏密上。m(t)越大,则零点越多。FM信号零点的变化规律直接反映了m(t)的变化规律,而PM信号零点的变化规律不直接反映m(t)的变化规律,而是反映m(t)的斜率变化规律。

③单音正弦波调制时,PM和FM信号的波形是很难区分的,它们有着密切的关系。

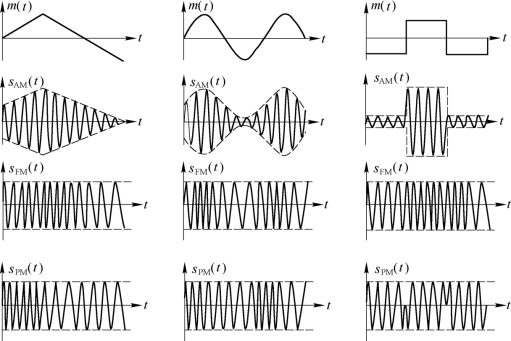
图4.4.1　AM、FM、PM波形

4.窄带角度调制

前面只确定了调相波和调频波的时间表达式,而没有给出它们的频谱,这是因为式(4.4.5)和式(4.4.10)对于任意调制信号的展开是比较困难的。但是如果对它们的最大相位偏移加以限制,其情况就简单得多。下面给出窄带角度调制的概念,随后再讨论其频谱。

窄带角度调制分为窄带调频(NBFM)和窄带调相(NBPM)。这里需要说明的是从频谱来看,它们都属于线性调制。

在角度调制表达式(4.4.4)中,如果最大相位偏移满足下面的条件:

则称其为窄带角度调制。

(1)窄带调频

如果调频信号的最大相位偏移满足下面的条件:

则称其为窄带调频。

在窄带调频中,可以求出它的任意调制信号的频谱表示式。如果最大相位偏移比较大,这时,调频信号的频谱比较宽,属于宽带调频(WBFM)。

把窄带调频的条件应用于式(4.4.10)并对其展开,得

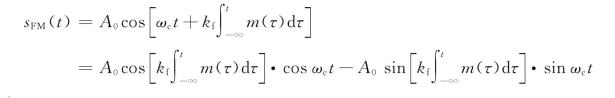
因为(或0.5rad),此条件下可以有下式成立,

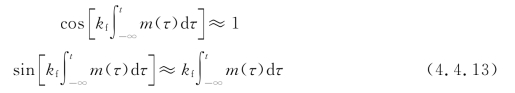
则FM信号的表达式就变为NBFM信号表达式,即

(2)窄带调相

同样,如果调相信号的最大相位偏移满足下面的条件

则称其为窄带调相。

如果最大相位偏移不满足上式,此时调相信号的频谱比较宽,属于宽带调相(WBPM)。

与窄带调频分析基本一样,可以得到窄带调相的表达式为

5.窄带调频的频谱和带宽

对公式(4.4.14)进行傅里叶变换,再利用傅里叶变换公式,有

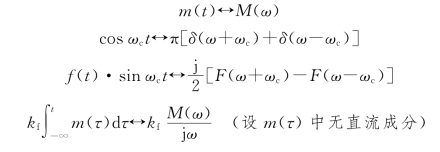(www.xing528.com)

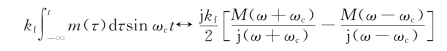
可以得到NBFM的频谱为

可以看出,NBFM信号的频谱是由±ωc处的载频和位于载频两侧的边频组成。与AM信号的频谱

相比较,两者很相似,所不同的是NBFM的两个边频在正频域内乘了一个系数1/(ω-ωc),在负频域内乘了一个系数1/(ω+ωc),而且负频域的边带频域相位倒转180°。

NBFM信号的频带宽度与AM信号的一样,为

NBFM信号的最大相位偏移很小,使得调频系统抗干扰性能强的优点不能充分发挥出来,因此,应用受到限制,只用于抗干扰性能要求不高的短距离的通信,或作为宽带调频的前置级,即先进行窄带调频,然后再倍频,变成宽带调频信号。

6.宽带调频的频谱与带宽

宽带调频信号的频谱分析,由于其调频信号展开式不能作像窄带调频时那样的处理,因而给频谱分析带来了困难。问题集中在对如何处理上。为了使问题简化,分析思路是:先假设m(t)为单音调制,求出单音调制时的WBFM的频谱表示式以及带宽。如果调制信号不是单音信号,而是任意的波形,对于调制信号则是周期性的任意信号,则可用傅里叶级数分解,相当于多个单音信号之和。这样,可把单音调制时的结论加以推广应用。如果任意信号是随机信号的话,则分析将会更复杂,本书对这类情况不作讨论。

(1)单音调制时的频谱和带宽

设单音调制信号为m(t)=Amcosωmt,则

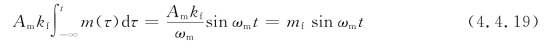
式中,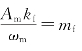是调频信号的最大相位偏移,也称其为调频指数。利用三角公式展开式(4.4.10),此时调频信号的表达式为

将两个因子cos(mfsinωmt)和sin(mfsinωmt)分别展开成傅里叶级数的形式,有

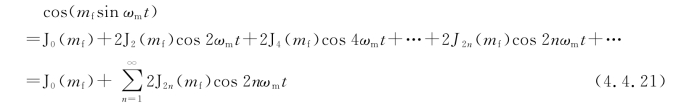
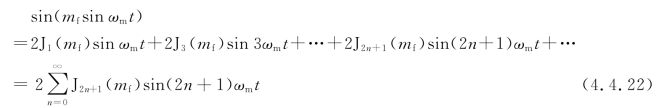
式中,Jn(mf)称为n阶第一类贝塞尔(Bessel)函数,

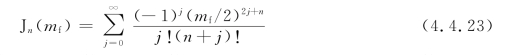
可以看出,贝塞尔函数是调频指数mf的函数,图4.4.2是Jn(mf)随调频指数变化的关系曲线。这里包括n=0到n=5(详细数据可参见贝塞尔函数表)。

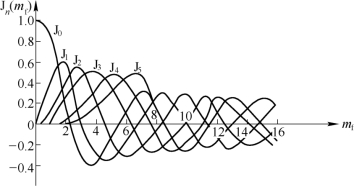
图4.4.2　Jn(mf)关系曲线

将式(4.4.21)和式(4.4.22)代入式(4.4.20),并利用积化和差的三角公式,可得

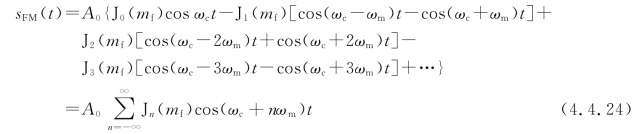
在式(4.4.24)中利用了

式(4.4.25)说明在n为奇数时,分布在载频附近的上下边频幅度具有相反的符号;而在n为偶数时,它们具有相同的符号;n=0时就是载频本身的幅度J0(mf)。调频信号的频谱如图4.4.3所示。

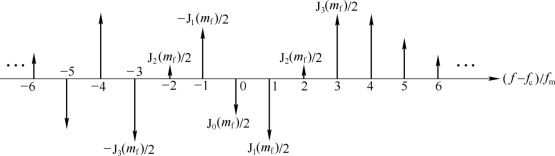
图4.4.3　调频信号的频谱(mf=5,fc≫fm)

由式(4.4.24)可见,即使在单音调制的情况下,FM信号也是由无限多个频率分量所组成,或者说,FM信号的频谱可以扩展到无限宽。这点是宽带调频与窄带调频以及AM信号频谱的明显区别。

实际上无限多个频率分量是不必要的。因为贝塞尔函数Jn(mf)的值随着阶数n的增大而下降,因此,只要取适当的n值,可以使│Jn(mf)│下降到可以忽略的程度,则比它更高的边频分量就可以完全略去不计,使调频信号的频谱约束在有限的频谱范围之内。通常认为,在有限频带内的功率占总功率的98%以上,则解调后的信号不会有明显的失真。如果考虑在有限频带内的功率为总功率的98%～99%,那么可以把边频幅度为未调载波幅度的10%～15%以下的那些分量忽略掉。当mf≥1以后,取边频数n=mf+1即可,因为n＞mf+1以上的Jn(mf)值均小于0.1,此时ωc±nωm成分产生的功率均在总功率的2%以下,这样就可以略去不计n＞mf+1以上的Jn(mf)值。

如果把幅度小于0.1倍载波幅度的边频忽略不计,则可以得到调频信号的带宽为

式中,Δf=mffm称为最大频偏,单位为Hz。如果mf≥10,则FM信号的频带宽度公式通常可以简化为

(2)双频及多频调制时FM信号的频谱

设双频调制信号为

由FM信号的一般表达式(4.4.10)可得

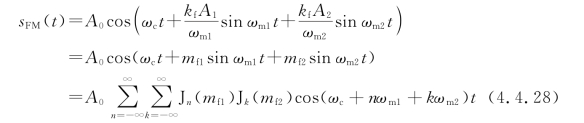
则双频调制信号时FM信号的频谱为

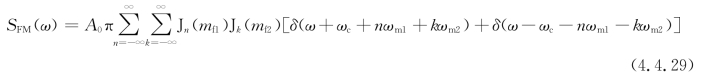
可以看出,双频调制时的FM信号频谱并不是两个单频调制的FM信号频谱的线性叠加,它有无穷多个交叉频率分量。而线性调制中双频信号调制的频谱则是两个单频调制频谱的线性叠加,这是两者的本质差别。

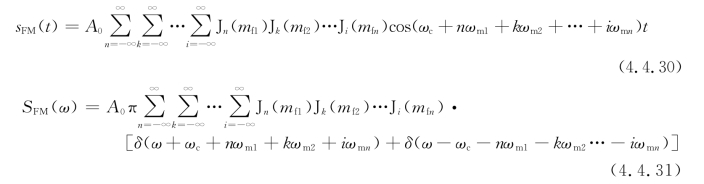
对于n个单频信号时,FM信号有相似的结果,随着调制信号中频率分量的增加,FM信号中的交叉分量急剧增加。

(3)周期性调制信号时调频信号的频谱和带宽

周期性信号可以用傅里叶级数分解为无穷多个频率分量之和,如果只取其中有限项则可以用多频调制表达式(4.4.31)计算出调频信号的各个边频分量。当所取频率分量项数较大时,式(4.4.31)的计算是非常复杂的。FM信号的频谱可用下式计算:

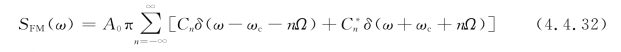
式中,Ω是调制信号m(t)的基频,m(t)的周期为T=2π/Ω;Cn是函数q(t)的傅里叶系数;C*n是函数q*(t)的傅里叶系数,q(t)和q*(t)互为复共轭。

任意FM信号频带宽度的一般应用近似(经验)公式为

式中,fm是基带调制信号的最高频率;D=Δf/fm,Δf为最大频偏。

(4)随机信号调频的谱密度函数

当调制信号m(t)是一个均值为零,幅度的概率密度函数为f(ρ)的随机信号时,FM信号的功率谱密度函数为

式中,为FM信号的平均功率。

以上讨论了FM信号的频谱分析及频带宽度,对于PM信号有相似的分析方法和相似的结论,限于篇幅这里不作讨论。

7.调频信号的平均功率

因为FM信号的表达式(4.4.10)是Acosx的形式,因此直接可以求出FM信号的平均功率为

另外,由贝塞尔函数的性质可知,对于任意的调频指数mf有

所以单音调频信号的平均功率为

实际上,从调频波形图可以比较直观地看到,当载波频率远大于调制频率时,调频波的疏密变化是缓慢的,在调制周期内,调频信号的平均功率等于未调制时的载波功率。

宽带调频有着广泛的应用,虽然它的频谱较宽,但却换来了较强的抗干扰性能,如FM广播就比振幅调制广播的音质好。调频常应用于远距离、高质量的通信系统,如微波接力通信、卫星通信以及优质调频广播与高保真信号的传输中。