相干解调系统性能分析方法与优化策略

采用相干解调法解调各种信号的抗噪声性能的分析模型如图4.3.2所示。其中输入信号sm(t)是指接收端的信号,也就是解调器输入端的信号,即是sAM(t)、sDSB(t)、sSSB(t)和sVSB(t)。

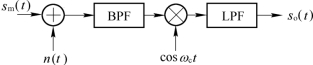
图4.3.2　相干解调分析模型

噪声n(t)是信道噪声和接收机、发射机中噪声的集中表示。通常认为它是加性高斯白噪声,其均值为零,双边功率谱密度为n0/2。

由于接收机的输入电路、高放、中放等可以等效为理想的带通滤波器,可以保证已调信号无失真地顺利通过,而带外噪声被抑制掉。因此,通过带通滤波器(BPF)后的信号和接收机输入信号sm(t)相同,而通过BPF后的噪声由高斯白噪声变为窄带高斯白噪声(简称窄带高斯噪声)。这是因为,BPF的中心频率与其频带宽度相比非常的大,如对于中波广播,中心频率为几百到几兆赫兹,而频带宽度则为4kHz,因此它是一个窄带系统。

本地载波cosωct应该与接收到的信号的载波完全同步。这不仅是指收端本地载波信号与发送端载波信号同频同相,而且是指发送端的已调信号的载波,通过信道传输后到达解调器输入端时,载波的频率与相位同本地载波的频率与相位完全一样。

低通滤波器LPF仅让调制信号的频谱通过,而抑制载频及其他高次项成分。

下面分别对AM、DSB、SSB和VSB信号在解调器的输入端、输出端的信号的平均功率、噪声平均功率进行分析计算,从而得出输入信噪比、输出信噪比和调制制度增益,以便比较这四种线性调制系统抗噪声性能。

1.DSB调制系统的性能

(1)输入信噪比

根据前面的假设,到达解调器输入端的DSB信号平均功率信号为

因为解调器输入端的噪声(用ni(t)表示)为窄带高斯白噪声,双边噪声功率谱密度为n0/2。所以解调器输入端的噪声平均功率Ni为

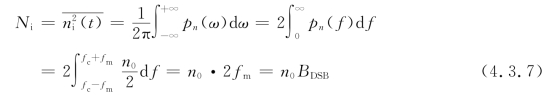
式(4.3.7)带有普遍性,计算各种已调信号在解调器输入端的噪声功率都是如此。由式(4.3.6)和式(4.3.7)可以方便地得出输入信噪比为

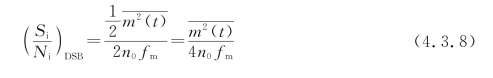
(2)输出信噪比

要计算解调器输出端的信噪比,必须先写出输出端的信号与噪声的表达式。在图4.3.2中BPF的输出端,信号加噪声的表达式为

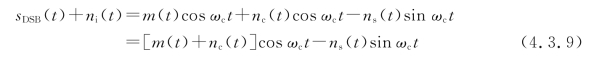
通过乘法器后表达式为

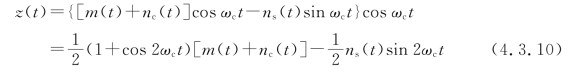
通过低通滤波器,滤去上式中的二次谐波(2ωc)成分,取出调制信号及相应的噪声,即得

由式(4.3.11)可以算出解调器输出端的信号平均功率为

解调器输出端的噪声平均功率为

根据式(2.6.20),可得

所以

这样得到的解调器输出端信噪比为

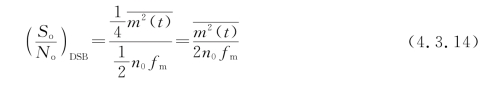
(3)调制制度增益

式(4.3.8)与式(4.3.14)相除,得到DSB信号的调制制度增益为

由此可知,DSB调制的制度增益为2。也就是说,DSB解调后输出信噪比So/No增加一倍,这是因为采用同步解调法后滤去了正交成分的噪声。

2.AM系统的性能

(1)输入信噪比

分析方法基本与DSB相似,解调器输入端的信号平均功率为

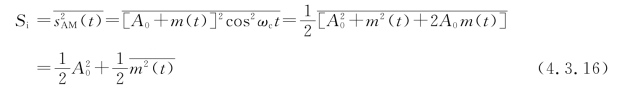
式中,表示AM信号的载波功率,表示AM信号的两个边带功率。

根据式(4.3.7),解调器输入端的噪声平均功率为

因此,解调器输入端的信噪比为

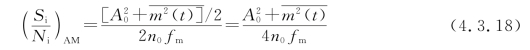
同理,可以求出解调器输出端信号功率比。

(2)输出信噪比

在图4.3.2中BPF的输出端,信号加噪声的表达式为

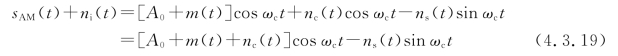
通过乘法器后表达式为

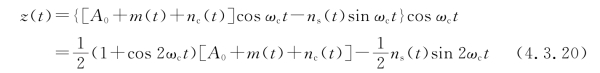
通过低通滤波器,滤去上式中的二次谐波(2ωc)成分,取出调制信号及相应的噪声,即得(www.xing528.com)

注意式(4.3.21)中,第三项是噪声;第二项是解调出的信号;第一项不能算信号,也不能算噪声,它可以通过隔直流电容滤除掉。所以解调器输出端的信号平均功率为

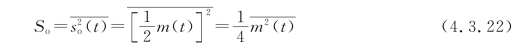
解调器输出端的噪声平均功率为

这样得到的解调器输出端的信噪比为

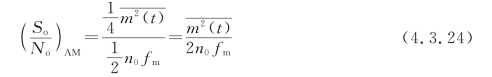
(3)调制制度增益

AM的调制制度增益为

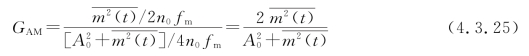
可以看出,由于载波幅度A0一般比调制信号幅度大,所以,AM信号的调制制度增益通常小于1。对于单音调制信号,即m(t)=AmcosΩt,则

如果采用满调幅,即A0=Am,此时调制制度增益最大值为

式(4.3.27)表示AM调制系统的调制制度增益在单音频调制时最多为2/3,因此AM系统的抗噪声性能没有DSB系统的抗噪声性能好。

3.SSB调制系统性能

(1)输入信噪比

已知单边带信号的表达式为

其中符号“-”表示上边带,符号“+”表示下边带。解调器输入端SSB信号的平均功率为

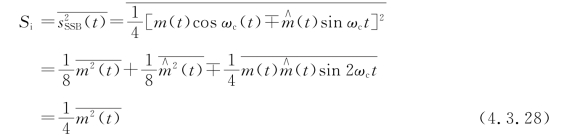
SSB信号解调器输入端的噪声平均功率为

这样,解调器输入端的信噪比

把SSB解调器输入信噪比公式(4.3.30)与DSB解调器输入信噪比公式(4.3.8)进行比较,可以看出它们一样,这是完全合乎实际情况的。虽然单边带信号是双边带信号的一半,但单边带系统的带宽也是双边带系统的一半,因此它们的输入信噪比应该是一样的。

(2)输出信噪比

结合相干解调法的性能分析模型,先分析SSB信号加上噪声后在解调器中各点的数学表达式,随后根据输出表达式求出输出信号与噪声的平均功率。

SSB信号加上噪声的表达式为

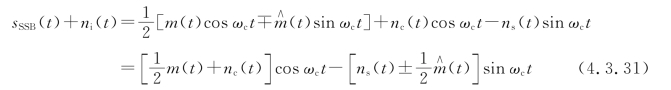
信号叠加噪声进入乘法器,乘法器的输出表达式为

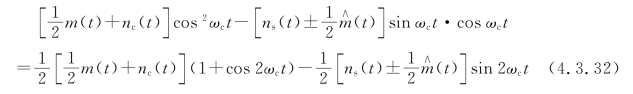
通过低通滤波器后,取出恢复后的调制信号和噪声为

所以,解调器输出端的信号平均功率为

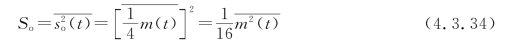
解调器输出端的平均噪声功率为

故解调器输出信噪比为

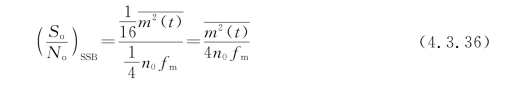
可以求得SSB信号的调制制度增益为

比较式(4.3.15)与式(4.3.37)可以看出,DSB解调器的信噪比增益是SSB的两倍。造成这个结果的原因是单边带信号中的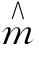(t)sinωct分量被解调器滤除了,而在输入端它却是SSB信号功率的组成部分。

因为双边带调制制度增益等于2,单边带调制制度增益等于1,所以双边带解调性能比单边带解调性能好一倍。这种说法是不正确的。因为,单边带信号所需频带是双边带信号的一半,因而在相同的噪声功率谱密度情况下,DSB解调器的输入功率是SSB的两倍。因此,尽管双边带解调器的调制制度增益是单边带的一倍,但它的实际解调性能不会优于单边带解调性能。如果解调器输入噪声功率谱密度相同,且输入信号功率相同,则单边带解调性能与双边带解调性能是相同的。

4.VSB调制系统性能

残留边带信号的表达式与单边带信号的表达式形式相似,只要把SSB信号表达式中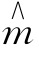(t)用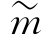(t)替换即可,因此整个分析过程完全与单边带信号的一样。下面的讨论仅给出结论。

(1)输入信噪比

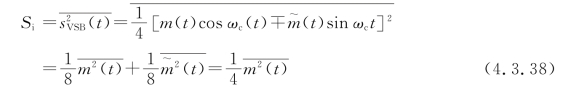
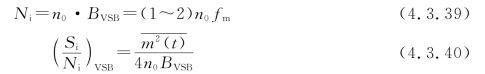
(2)输出信噪比

在解调器输出端,即通过低通滤波器后输出信号与噪声的表达式为

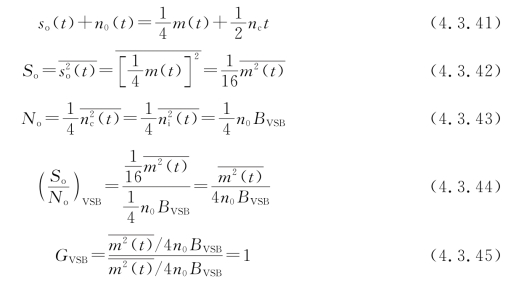
比较式(4.3.45)与式(4.3.37)可以看出,VSB解调器的信噪比增益与SSB的信噪比增益一样,都等于1。