正弦波加窄带高斯过程的统计特性分析

(1)正弦波加窄带高斯过程的同相分量和正交分量的联合概率密度函数

在正弦信号初相位θ给定的情况下,由前面的分析可知,接收信号r(t)的同相分量和正交分量的联合概率密度函数f(x,y|θ),是同相和正交二分量一维概率密度函数f(x|θ)和f(y|θ)之积,而它们二者都符合高斯分布,因此需先求出高斯分布的均值和方差

这里用到了零均值平稳窄带高斯过程的同相分量和正交分量的均值也是零的性质。

同理可得

同理可得

因此,接收信号r(t)的同相分量和正交分量在θ给定条件下的联合概率密度函数f(x,y|θ)为

(2)正弦信号加窄带高斯过程的包络和相位的概率密度函数

①正弦信号加窄带高斯过程的包络的概率密度函数

由式(2.8.9)和概率论的知识,可以得到在θ给定的条件下,接收信号r(t)的包络和相位的联合概率密度函数为

利用式(2.8.4)得到

将式(2.8.9)代入上式得

利用式(2.8.3)得到

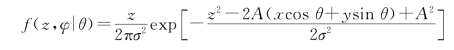
利用式(2.8.4)得到

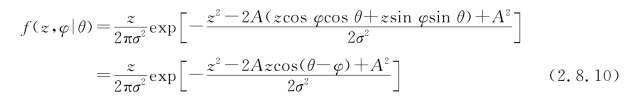
求边际条件,可以得到在θ给定的条件下,接收信号r(t)的包络的一维概率密度函数为

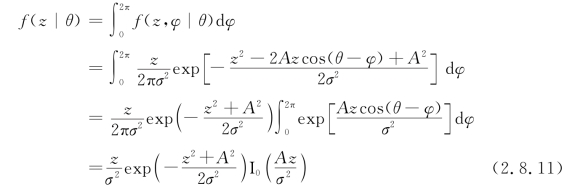
式中,I0是零阶修正贝塞尔函数:(www.xing528.com)

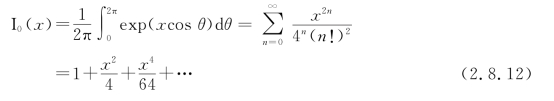
由式(2.8.11)可以看出f(z|θ)与θ无关,因此可以得到正弦信号加窄带高斯噪声包络的概率密度函数为

式(2.8.13)称为莱斯分布函数,也称广义瑞利分布。由式(2.8.12)可以得到,当x≪1时,

当x≫1时,

可以由式(2.8.14)和(2.8.15)来讨论并简化式(2.8.13):

当x≪1(对应着A≈0,即有用信号近似为零,信噪比很低)时,I0(x)|x→0≈1,此时,接收信号包络的概率密度函数为

式(2.8.16)说明,在信噪比很低的情况下,正弦信号加窄带高斯噪声信号的包络的概率密度函数f(z)近似为瑞利分布,与窄带高斯噪声的包络的概率密度函数相同,如图2.8.1所示。

当x≫1(对应着有用信号相对于窄带噪声较大,z≈A,信噪比较大)时,由式(2.8.15)可化简接收信号包络的概率密度函数f(z)近似为

式(2.8.17)说明,在大信噪比的情况下,正弦信号加窄带高斯噪声的包络的概率密度函数f(z)近似为高斯分布,如图2.8.1所示。

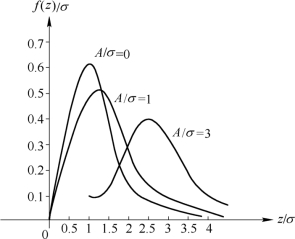
图2.8.1　正弦信号加窄带高斯噪声信号的包络分布

图2.8.1给出了正弦信号加窄带高斯噪声信号的包络分布。正弦信号的平均功率是A2/2,零均值窄带噪声信号的平均功率是σ2,因此A/σ可以看作接收端接收信号的信噪比。图2.8.1给出了随信噪比变化的一族包络分布函数的曲线。

结论:正弦信号加窄带高斯噪声的包络分布与信道输出的信噪比有关。在小信噪比时,它服从瑞利分布;在大信噪比时,它服从高斯分布;信噪比介于以上两者之间的,则服从莱斯分布。

②正弦波加窄带高斯过程的相位的概率密度函数

正弦波加窄带高斯过程的相位的概率密度函数f(φ|θ)的推导比较复杂,在此不作推导,只给出结论。

正弦信号加窄带高斯噪声信号的相位分布与信道输出的信噪比有关。在小信噪比时,它近似服从均匀分布;在大信噪比时,随机相位主要集中在信号相位附近,如图2.8.2所示。

图2.8.2显示出了正弦信号加窄带高斯噪声信号的相位分布随接收端接收信号的信噪比变化的一族曲线。

图2.8.2　正弦信号加窄带高斯噪声信号的相位分布