高斯过程的一维统计特性分析

(1)高斯过程在时间t得到一随机变量ξ(t),其概率密度函数为

它是高斯过程的一维统计特性,其中a、σ2(分别表示该随机变量的均值和方差)是常数。f(x)如图2.5.1所示。

一维概率密度函数具有以下特性:

①f(x)对称于直线x=a,即f(a+x)=f(a-x);

②f(x)在(-∞,a)上单调增,在(a,+∞)上单调减,在a点处有最大值当x→±∞时,f(x)→0;

图2.5.1　高斯过程的一维概率密度函数

③

且

④当σ2不变,a改变时,f(x)的形状不变,只是左右平移,即a增大向右,a减小向左;当a不变,σ2改变时,f(x)的位置不变,形状改变,即随σ2的增大而变矮变宽,随σ2的减小而变高变窄;

⑤当a=0,σ2=1时,有

称这种高斯分布为标准高斯分布。

(2)高斯过程在时间t得到一随机变量ξ(t)的分布函数为

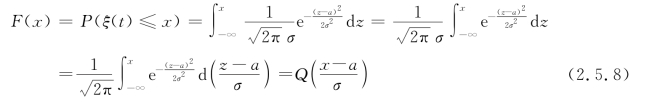
式中,Q(x)是概率积分函数,其定义如下:

(www.xing528.com)

概率积分函数的求解可以通过查表得到近似值,见附录C。

(3)用误差函数或误差互补函数表示分布函数

误差函数erfx定义如下:

误差互补函数erfcx定义如下:

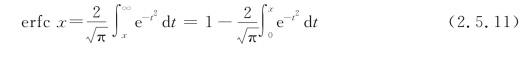
当x≥a时,

证

当x≤a时,

证

例2.5.2 有一高斯平稳过程,均值是0,相关函数为,试求在时刻t1,随机变量ξ(t1)取值大于0.5的概率。

解 依题意,高斯过程的均值a=0,均方值,所以,方差为

因此,随机变量ξ(t1)取值大于0.5的概率为