在通信技术中,常常面对的是随时间而变化的随机变量,实际上,这就是随机过程的通俗解释。下面通过一个例子来更深入地理解随机过程的概念。
例如:有一个仪器厂,要对n台同样型号的示波器进行同一条件的测试,第一台的测试结果如图2.3.1的x1(t)所示,第二台的测试结果如x2(t)所示,第n台的测试结果如xn(t)所示,那么,x1(t),x2(t),…,xn(t),…即为若干次随机试验样本,如果每一个试验样本xi(t)都对应一个样本函数si,所有可能的样本函数{si},i=1,2,…,n,…构成了样本空间S。则可以说,就一次观察来看,试验结果肯定是所有可能波形中的一个,而所有可能的波形x1(t),x2(t),…xn(t),…的集合{xi(t)},i=1,2,…,n,…构成了随机过程ξ(t)。
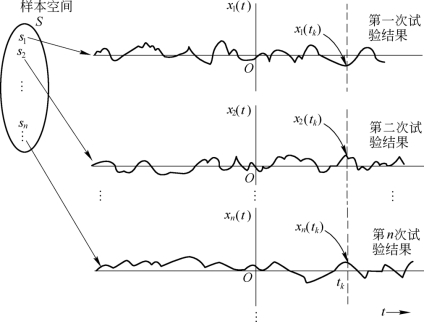
图2.3.1 n次随机试验的试验结果
在图2.3.1中,选tk时刻观察随机过程,在整个样本空间S中,得到样值集x1(tk),x2(tk),…,xn(tk),…,或{xi(tk)},i=1,2,…,n,…是一个随机变量,即随机过程在tk时刻的量ξ(tk)是一个随机变量。同理,随机过程在t1,t2,…,tn时刻,分别是随机变量ξ(t1),ξ(t2),…,ξ(tn)。因此可以说,随时间t变化的随机变量的全体就是随机过程。下面给出随机过程的两种定义。
定义1 设E是随机试验,样本空间S={s},参数集T⊂(-∞,+∞),如果对于每一个s∈S,总有一个确定的时间函数ξ(s,t)与之对应,这样对于所有的s∈S,就可以得到一族时间t的函数,称{ξ(s,t),t∈T}为随机过程。
定义2 设E是随机试验,样本空间S={s},参数集T⊂(-∞,+∞),如果对于每一个t∈T,总有一个定义在S上的随机变量ξ(s,t)与之对应,则称{ξ(s,t),t∈T}为随机过程。
在不产生混淆的情况下,{ξ(s,t),t∈T}简记为ξ(t)。
注:如把ξ(s,t)当作二元函数,则{ξ(s,t),t∈T}有如下含义:(https://www.xing528.com)
(1)当t∈T取定,ξ(s,t)是一随机变量,那么{ξ(s,t),t∈T}是一族随机变量。
(2)当s∈S取定,ξ(s,t)是一自变量为t,定义域为T的普通函数,那么{ξ(s,t),t∈T}是一族确定函数。
(3)当t∈T,s∈S取定,则ξ(s,t)是一确定数值。
(4)为了方便,也常将符合随机过程定义的信号称为随机信号。
例2.3.1 考察信号ξ(t)=acos(ωt+θ),其中:a,ω是常数,t∈(-∞,+∞),θ是(0,2π)上均匀分布的随机变量。
解 对某一时刻t=t1,ξ(t1)=acos(ωt1+θ)是一随机变量,取若干时刻,则得到一族随机变量。
如果在(0,2π)内随机取一个数θ1,就可以得到这个随机过程的一个样本函数,ξ1(t)=acos(ωt+θ1),其中t∈(-∞,+∞),取若干个相位,则得到一族确知函数。
所以{ξ(t)}是一随机过程。一般称该信号为随机相位正弦波。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




