【摘要】：分布函数F的主要性质①F是一个不减函数,因此,对于任意实数x1,x2,有②0≤F≤1,且2.离散型随机变量的概率分布概念若随机变量X的全部可能取值为有限个或可列无限多个,则称X为离散型随机变量。
1.随机变量与分布函数
(1)概念
设随机试验E,样本空间S,在S上定义一个单值实函数X=X(ω),ω∈S,如对∀x∈R,事件{X≤x}={ω:X(ω)≤x}总有确定的概率,则称X为随机变量,称函数F(x)=P{X≤x}为随机变量X的分布函数。
(2)分布函数F(x)的主要性质
①F(x)是一个不减函数,因此,对于任意实数x1,x2(x1＜x2),有
②0≤F(x)≤1,且
2.离散型随机变量的概率分布
(1)概念
若随机变量X的全部可能取值为有限个或可列无限多个,则称X为离散型随机变量。其概率分布(或称分布律)为:P{X=xi}=pi,i=1,2,…,可以用表格表示为:
(2)离散型随机变量分布律的基本性质(www.xing528.com)
(3)离散型随机变量的分布函数
离散型随机变量的分布函数为
F(x)是一个取值在[0,1]上的非减阶梯函数,在x=xi处跳变,跳变值为pi=F(xi)-F(xi-1),i=1,2,…。
3.连续型随机变量的概率分布
(1)概念
若对随机变量X的分布函数F(x),存在非负可积函数f(x),使得对任意实数x,有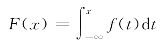
成立,则称X为连续型随机变量,函数f(x)称为X的概率密度函数。
(2)X的概率密度函数f(x)的主要性质
③对任意常数a＜b,有
④在f(x)的连续点处,
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
