硬相微粒钉扎奥氏体晶界的作用

用铝脱氧的钢及含有Nb、V、Ti等元素的钢，存在AlN、NbC、VC、TiC等微粒。这些析出相硬度很高，难以变形，存在于晶界上时会阻止奥氏体晶界移动，对晶界起了钉扎作用，可在一定温度范围内保持奥氏体晶粒细小。

如果在奥氏体晶界上有一个硬相微粒，设为球形，半径为r，如图11-9所示。它与奥氏体的相界面的面积为4πr²，界面能为4πr²σ_相。由于晶界向前移动，晶界从Ⅰ位置移到Ⅱ位置，则造成晶界的弯曲、变长，增加的相界面面积为S，晶界能发生变化，故界面能升高为Sσ。这是一个非自发过程，所以移动困难，受到了一定的移动阻力。

晶界弯曲的几何证明如下：在晶界与微粒的交点处，当三个界面处于平衡状态时，则有

因此，θ₁＝θ₂，即晶界与微粒相界面应当垂直，那么离开微粒的晶界必然弯曲。这使得奥氏体晶粒交界面的面积增加，使能量升高，等于阻止晶界右移，相当于有一个阻力G作用于奥氏体晶界。

图11-9 细小颗粒相与晶界之间交互作用示意图

设晶界从Ⅰ位置移到Ⅱ位置，晶界暂停移动，处于平衡态。那么，阻力的大小必须等于界面总张力在水平方向上的分力，即与σ在水平方向的分力相平衡。

微粒与晶粒相接触的周界长度L＝2πrcosφ，则总的线张力F_总＝2πrcosφσ′，在水平方向上的分力F_分＝2πrcosφσ′sinβ。已知β＝90°＋φ－α，所以

F_分＝2πrcosφσ′cos（α－φ） （11-4）(www.xing528.com)

式中 α——常数，其值与相界能有关；

φ——变量，随晶界与微粒的相对位置不同而变化。

平衡时，阻力G＝F_分。可见，F_分是φ的函数，φF_分＝f（φ）。可以求出φ变化时的最大阻力，取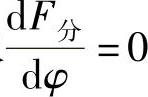，计算得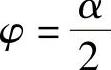时阻力最大，即

G_m＝F_max＝πrσ′（1＋cosα） （11-5）

设单位体积中有N个半径为r的微粒，所占的体积分数为f，则可以证明最大阻力为

当α＝90°、φ＝45°时，最大阻力为

可见，如果是一个微粒，其半径r越小，则最大阻力越大。在钢中往往存在较多的硬相微粒，当其体积分数f一定时，微粒越细，半径r越小，微粒数量越多，则对于晶界移动的阻力越大。第二相微细颗粒具有细化晶粒的作用。