合金钢钢坯退火工艺的有限差分法计算机辅助设计

在冶金厂生产的钢材不仅有棒材，而且还有方断面和长方断面的钢坯。对于一些合金钢钢坯，轧制后要进行退火。这些钢坯的长度较长，为了提高退火质量，目前多采用辊底式退火炉进行退火^[4]。

钢坯在辊底式炉中加热时，其传热可采用直角坐标导热方程表示

下面首先讨论直角坐标系的差分方程。

1.直角坐标系的有限差分方程

图9-14所示为在均匀网格三维直角坐标系中，围绕P点的单元控制体积及六个相邻点W、E、N、S、I、O。在直角坐标系中，差分方程的推导也有两种基本方法，即偏微分方程替代法和能量平衡法。

（1）偏微分方程替代法 在整个求解区域上布置均匀网格系统，且有均匀热导率的三维导热区域。取Δx＝Δy＝Δz，且无内热源。基本微分方程为

式中，

下面求图9-14中所示P点的差分方程。用显式差分方程表示时，方程的左端取时间t时刻的值，右端用向前差分表示，它只包含在P点的T（t＋Δt）与T（t）。P点的显式差分方程式为

图9-14 均匀网格的三维直角坐标中围绕P点的单元控制体积及六个相邻点

式中，T_P′＝T_P（t＋Δt）；T_P＝T_P（t），为t时刻的值。

式（9-53）也可简化为

式中 F₀-傅里叶数，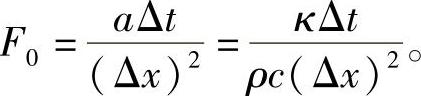

对于二维（x，y）导热区域，同样可推导出相似的公式

一维（x）的热流公式为

P点的隐式差分方程式为

可简化为

P点的中间差分格式为

所取之值＝λ（在t＋Δt的值）＋（1－λ）（在t的值）

三维传热问题可表示为

令λ＝0，1，0.5，分别恢复显式格式、完全隐式格式与克兰科-尼科尔森中间差分格式。

将式（9-59）整理后得

对于二维（x，y）和一维（x），类似的公式为以下两式

（2）能量平衡法 利用能量平衡法可以得到完全相同的P点的差分方程。同样取图9-14中的P点的单元控制体积，取均匀网格间距Δ＝Δx＝Δy＝Δz，控制体的六个侧面的面积为Δ²，P点周围六个点与P点的距离均为Δ，则由W点流向P点的热流为

式中 A_PW——与P点和W点之间热流方向垂直的平均表面积Δ²；

L_PW——两点之距Δ。

因此可得

由N点流向P点的热流为

由E点流向P点的热流为

由S点流向P点的热流为

由I点流向P点的热流为

由O点流向P点的热流为

从周围六个节点流向P点的总热流为

∑Q＝Q_PW＋Q_PN＋Q_PE＋Q_PS＋Q_PI＋Q_PO（9-63）

流入P点的热流将使其温度变化ΔT_P＝T_P′－T_P

所以有

式中 V_P——P点的控制体体积，V_P＝ΔxΔyΔz。

如果研究的物体中存在内热源，则必须把HV_P项加入到式（9-64）中。

式（9-64）通常能用作任何内部节点方程，而外部节点要考虑边界条件后推出差分方程。在式（9-64）中，

的取值方法不同将得到不同形式的有限差分方程，一般取作t～t＋Δt的向前差分

同样，式（9-65）左端项在不同的时间层取值，（t，t＋Δt）或两者之间的某时间层，后者由下式决定：λ（t＋Δt的值）＋（1－λ）（在t的值）。

式中，0≤λ≤1，λ＝0时为显式格式，λ＝1时为完全隐式格式，0＜λ＜1时为加权平均中间值，λ＝0.5时得到克兰科-尼科尔森格式。

将式（9-64）左端各项采用加权平均能量平衡公式，对公式右端采用向前差分，即式（9-65）的形式，其结果为[λκΔ（T′_O－T_P′）＋（1－λ）κΔ（T_O－T_P）]＋用I，N，S，E和W代表O的五个类似项

将式（9-66）整理后得

式（9-67）和式（9-59）完全一样。由二维和一维简化公式的导数得来的有限差分方程与式（9-60）、式（9-61）也完全一样。

如果引入内热源项，无论应用偏微分方程替代法或应用能量平衡法，都可得到相同的有限差分方程。

2.实际退火炉内钢坯加热的差分方程

在辊底式炉内加热钢件，钢件平放单摆入炉，且随炉内辊子的转动，钢件向前移动。长度z方向较宽度x、y方向大得多，且认为没有内热源。所以，钢件的传热可视为沿断面的二维传热，其传热方程如下

初始条件为

t＝0，T（x，y）＝T₀ （9-69）

边界条件为(www.xing528.com)

式中：T₀——钢件的初始温度，为常数；

к——钢件的热导率；

h——钢坯表面与炉气的对流换热系数；

Q_辐——钢坯与炉气、炉墙的辐射换热量；T_f、T_表——分别为炉气温度和钢坯表面温度。

钢件在炉内的加热左右对称，因此可只讨论断面的1/2，划分的格子如图9-15所示。设钢件断面宽为x、高为y，钢坯上、下及右边界与炉气、炉墙的热交换视为定热流q₁、q₂、q₃的边界条件。钢件的左边界为绝热边界。

图9-15 钢坯横断面格子划分

采用能量平衡法推出各节点的差分方程。如果在x、y方向不等分格子，则显式差分方程如下：

内部节点1的显式差分方程为

式中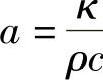，，dx、dy分别为x、y方向的网格间距。

右上角节点2的显式差分方程为

上边界节点3的显式差分方程为

左上角节点4的显式差分方程为

左边界节点5的显式差分方程为

左下角节点6的显式差分方程为

下边界节点7的显式差分方程为

右下角节点8的显式差分方程为

右边界节点9的显式差分方程为

（9-79）

3.边界条件的处理

钢件在炉内的加热是靠辐射管加热，即通过炉气的对流及炉气、炉墙的辐射传热。钢坯的上表面、侧面、下表面与炉气、炉墙的换热各不相同，因此，用q₁、q₂、q3分别表示。

钢件在炉内加热时，其运动速度较慢，一般为每小时几米。因此，可以把钢件表面与炉气的对流换热看成为自然对流。表面传热系数h用准数公式计算，同式（9-33），只是常数C、n的值不同。对于上表面，C＝0.58、n＝0.50；对于侧表面，C＝0.59、n＝0.25；对于下表面，C＝0.54、n＝0.25。

取700℃空气的热物性参数，查出P_r值，计算出G_r值，然后算出N_um，表面传热系数为

式中 λ₁——炉气的热导率；

L——定型尺寸，上下表面为钢坯的宽度，侧面为钢坯的厚度。

由式（9-80）可以计算出不同尺寸钢件的上、下表面及侧面的表面传热系数。

辐射换热是第二类边界条件，它包括两部分：①炉墙与钢件的辐射换热；②炉气与钢件的辐射换热。其中炉气与钢件的辐射换热可用式（9-35）计算，炉墙与钢件的辐射换热可用式（9-36）计算，只是式（9-37）中的φ_gs要重新计算，而且要针对三个不同的表面分别计算出相应的炉墙对钢件的角系数φ_gs。

4.差分方程计算机求解

（1）显示差分格式求解 二维显式差分格式的求解过程与前面讨论的一维显式差分格式的求解过程很相似。目前讨论的钢件加热是二维导热问题，其空间步长为dx和dy。钢件断面上各个节点的温度计算可利用式（9-71）～式（9-79）进行求解，求解出各个不同时刻的温度场是一个二维空间数组。

二维不稳态导热的计算采用显式格式时，必须满足

所以，只要时间步长Δt满足上述稳定性条件，即可得到稳定的解。

（2）隐式差分格式求解 对于二维不稳态导热问题，如式（9-69），其内部节点差分方程可写为

当λ＝0时，为显式差分格式。

当λ＝1时，为完全隐式格式，即

数学上可以证明，用完全隐式格式能保证解的绝对稳定，即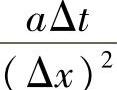取任意值都是稳定的。

当λ＝0.5时为十点差分格式，它相当于一维问题中的六点差分格式。数学上可以证明这种格式的绝对稳定性，其求解的方法与完全隐式格式相同。

当0＜λ＜0.5时，只有当时，其解才是稳定的。这种格式也是隐式格式，其求解方法与完全隐式格式一样。

实际上，二维非稳态导热的各种差分格式都可以用消元法或迭代法去解。但由于这些差分格式中所含有的未知量的个数往往很多，用一般的迭代法与消元法计算工作量都很大。因此，对于二维不稳定导热问题，一种极为方便的方法是交替方向隐式法，又称为ADI法。下面介绍ADI法的求解过程。

将导热微分方程式（9-68）应用于内部节点（i，j），写成如下形式

相应的差分方程为

以上从微分方程到差分方程的过程中，导热方程中温度对时间的偏微商仍用时间的向前差商代替，而温度对距离的二阶微商在x方向上用n＋1时刻，在y方向上用n时刻。这样处理这个差分方程仍是隐式的，但方程中只包含三个未知数，方程所对应方程组的系数矩阵具有三对角线的特点，可用追赶法求解。运用这种方法计算的工作量可减少很多，但格式的稳定性不再是无条件的。

为了既能保证格式的绝对稳定性，又使计算工作量不增加，可以在使用隐式格式时交替改变方向，即对一次Δt增量取x方向为隐式格式，而对下一次Δt增量取y方向为隐式格式。这样，每增加一次Δt它的计算工作量与上述单一方向使用隐式格式是完全相同的，这种格式的具体形式如下

数学上已证明，应用这种格式的稳定性是绝对的。方程组式（9-86）中第一个方程的未知数是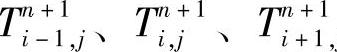j，第二个方程的未知数是。所以，方程组式（9-86）可以写成如下形式

式（9-87）可以展开为两个方程组，第一个方程组展开为式（9-88），第二个方程组展开为式（9-89）。

i＝1，2，…，l；j＝1，2，…，p。

i＝1，2，…，l；j＝1，2，…，p。

方程组式（9-88）和式（9-89）的追赶法求解过程与前述的一维传热追赶法求解过程相同。式（9-88）中j＝1，2，…，p，计算出追赶法运算系数U₁（i，j）、V₁（i，j）中的U₁（1，j）、V₁（1，j）

式（9-89）中i＝1，2，…，l，计算出追赶法运算系数U₂（i，j）、V₂（i，j）中的U₂（i，1）、V₂（i，1）

从而可利用ADI法方便地求解不稳态导热问题，其求解程序框图如图9-16所示，其中T（i，j）是n时刻的节点温度，T′（i，j）是n＋1时刻的温度。子程序1用于计算热导率及边界热流；子程序2用于x方向顺追赶法计算系数U₁（i，j）、V₁（i，j）；子程序3用于x方向逆追赶法计算节点温度T′（i，j）；子程序4用于y方向顺追赶法计算系数U₂（i，j）、V₂（i，j）；子程序5用于y方向逆追赶法计算节点温度T′（i，j）。

图9-16 利用ADI法求解二维不稳态导热问题程序框图