利用有限差分法进行合金钢棒材热处理工艺计算机辅助设计

冶金厂生产的合金钢棒材尺寸均较长，有7～8m长。以往热处理都是用台车式炉，其优点是装炉量大。但台车式炉在加热和冷却时，装在外部和内部的工件加热冷却不一致，因此，热处理后组织性能不均匀。同时，台车式炉加热和冷却时需用的时间长，氧化脱碳也较严重。针对这一情况，目前冶金厂均对炉子进行了改造，大部分采用先进的辊底式连续炉进行热处理。

棒材在辊底式炉中加热时，其导热可用极坐标导热方程表示，如图9-6所示。

对于圆棒钢材，当热导率为变量时，一般导热方程为

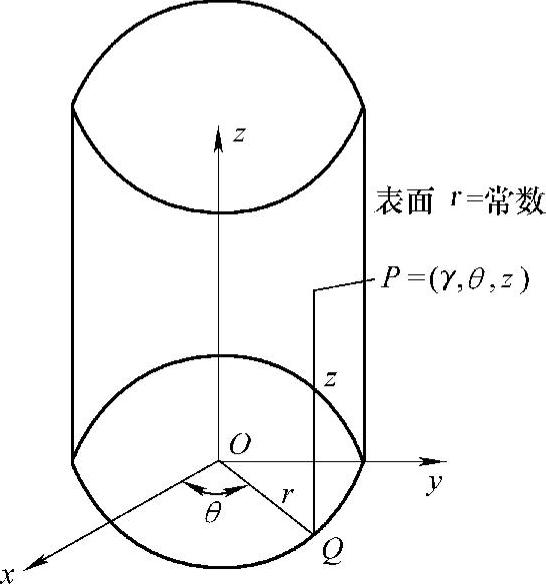
图9-6 圆柱极坐标系

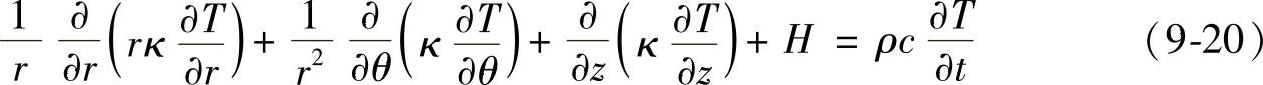
热导率为常数的导热方程为

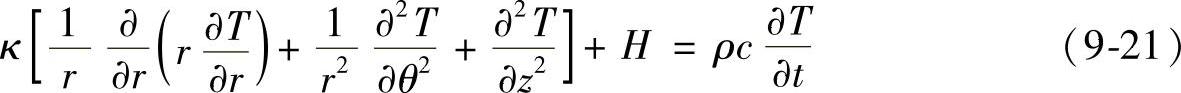
式中 T——温度；

t——时间；

κ——热导率；

H——单位体积内热量产生的速率；

θ——柱坐标的角度。

以上偏微分方程采用有限差分法求解时首先要建立有限差分方程，然后利用计算机计算进行求解。

1.柱面极坐标系传热计算的有限差分方程

差分方程的推导可以采用直接替代法和能量平衡法。

（1）直接替代法 直接替代法就是用有限差商代替微商直接得到的差分方程。讨论圆柱体时，可以取出其中的一个小单元，这个小单元在柱面极坐标中的几何图形如图9-7和图9-8所示，其中z、r、θ分别具有相等的增量。对式（9-21）直接差分方程式后，可得到0点的差分方程式为

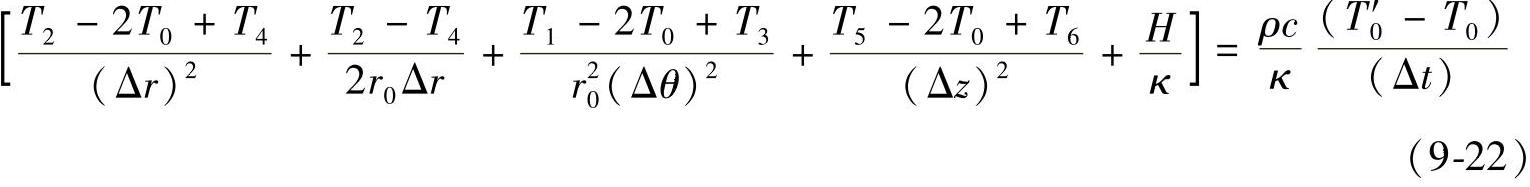
式（9-22）为完全显式差分格式方程。利用能量平衡法可得到完全的和局部的隐式差分形式。

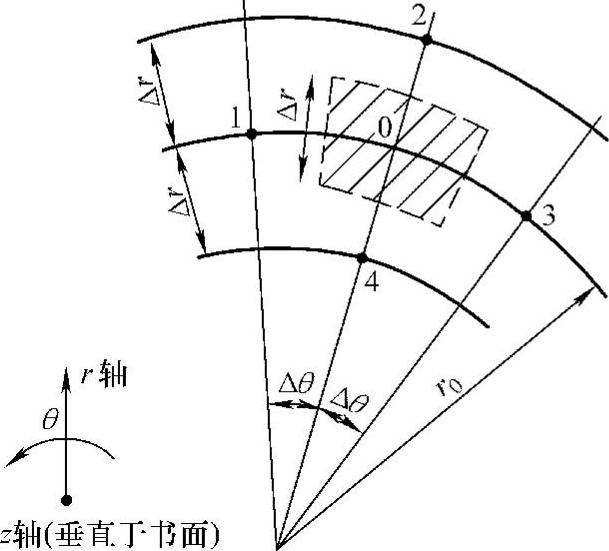
图9-7 柱面坐标

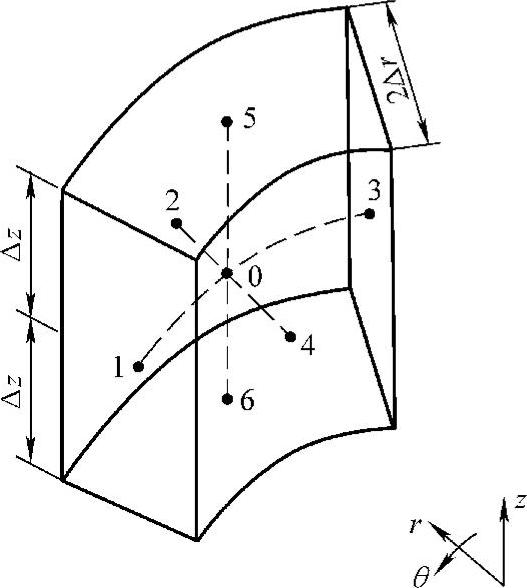
图9-8 以相等的r和θ增量细分圆柱体

（2）能量平衡法 对于图9-7、图9-8所示的小单元（控制体），可根据由节点0相邻各点传到0点的导热热流速率和0点所表示的控制体内的热源放热速率，以及控制体内的温度上升速率建立节点0的能量平衡，具体过程如下：

从1点到0点的导热热流速率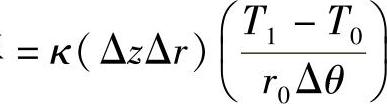

从2点到0点的导热热流速率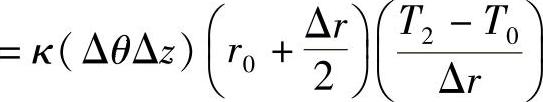

从3点到0点的导热热流速率

从4点到0点的导热热流速率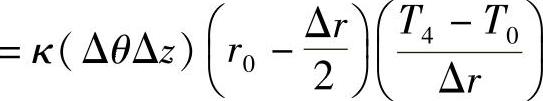

从5点到0点的导热热流速率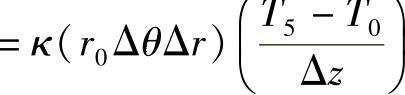

从6点到0点的导热热流速率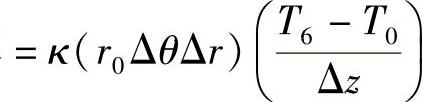

控制体内热源放热速率＝H×控制体体积＝H（r₀ΔθΔz） （9-24）

传到控制体的热量也可以用下式表示

Q_V＝（控制体的质量×比热容×节点温度的改变速率）

式（9-23）与式（9-24）之和等于式（9-25），整理后得到0点的完全能量平衡方程式为

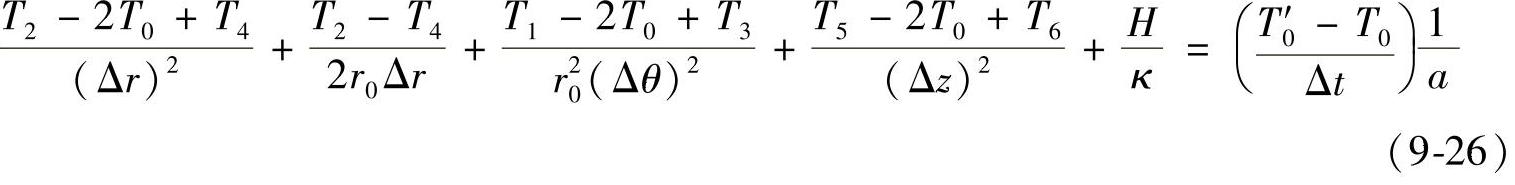
式中 a——导温系数，a＝κ/ρc。

可见，式（9-26）与式（9-22）完全一样。对于圆柱体的中心处节点，式（9-26）不适用。因为轴上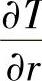＝0，因此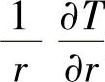，为不定值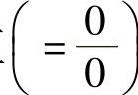。但是，利用罗比塔法则可以证明：当r→0时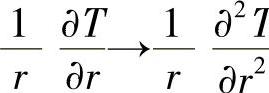，这个公式有定值（这一点前人已做了证明）。

假如圆柱体是轴对称的，即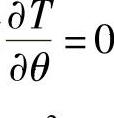，且H＝0，为稳定热流，则基本方程式为

在r＝0处，有

对于圆柱体轴对称且H＝0时，有限差分方程可以取最近邻点的温度作为r＝0处的温度。对于非轴对称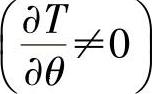的稳态导热问题，则把其周围各网格节点温度的平均值作为该处的温度。

如果将式（9-26）或式（9-22）中的左边各项按上一时间层进行计算，那么，整理后可以由前一时刻的0点及六个相邻点的温度来计算下一时刻的T₀′，这就是完全显式差分格式表示法。如果左边各项都以新的时间层进行计算下一时刻的T₀′，则得到完全隐式差分格式表达式。

2.实际退火过程中棒材导热计算的差分方程

在辊底式炉内加热棒材，且棒材是并排单摆入炉，长度z较半径r大得多，且无内热源（H＝0），则棒材的传热可视为沿圆断面的径向一维传热，方程式如下

初始条件：t＝0，T（r，0）＝T₀

边界条件：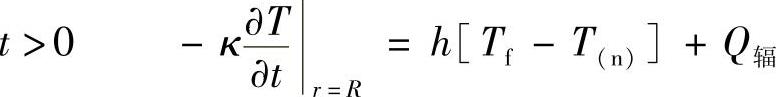

式中 T₀——棒材的初始温度，为常数；

κ——棒材的热导率；

h——棒材表面与炉气的表面传热系数；

Q_辐——棒材表面与炉墙、炉气的辐射换热量；

T_f、T（n）——分别为炉气温度和棒材的表面温度。

棒材沿直径方向的格点划分如图9-9所示。各节点的差分方程如下：

对于图9-9中的内部节点3，采用直接替代法得到的差分方程为

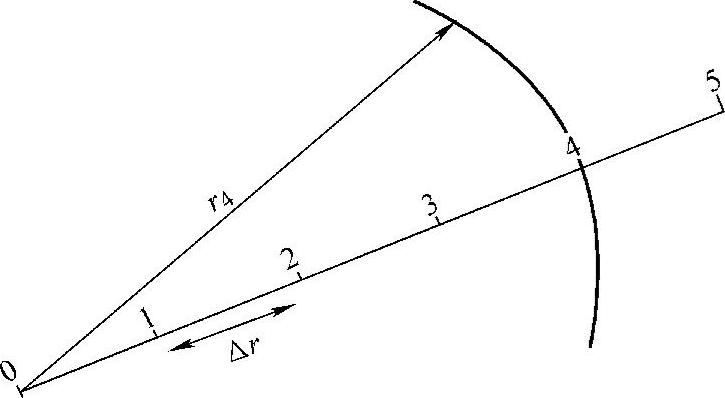
图9-9 棒材径向格点划分图

除了中心节点（0）和外表面节点（5）外，其余的每个节点（1～4）都具有类似的方程式。内部节点的差分方程式可写为

式中F₀——傅里叶数，对于中心节点0，，因此中心节点的差分方程式为

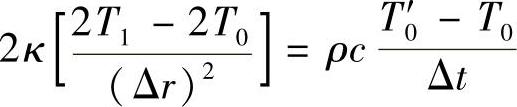
因此有

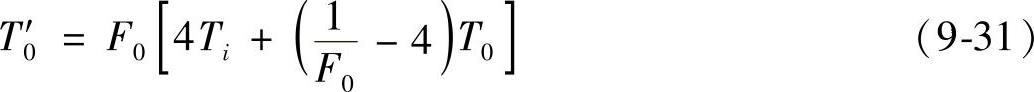
可将外部节点5视为外界有一恒定热流q_w加热棒材，利用能量平衡法推出差分方程为

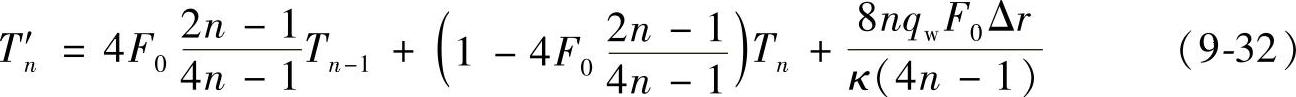
3.边界条件的处理

棒材在炉内的加热是以对流和辐射两种方式进行的。

对流换热是第三类边界条件，属于自然对流。表面传热系数h用N_um特征数方程计算

N_um＝C（G_rP_r）n_m（9-33）式中，N_um是努塞尔数；G_r是格拉晓夫数；P_r是普朗特数；C和n是由试验确定的常数；下标m表示定性温度，取边界层平均温度，即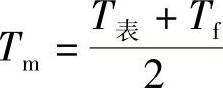。棒材在辊底式炉中的加热相当于大空间中的自然对流传热，查得C＝0.53、n＝0.25。

取700℃的空气热物性参数，查出P_r数，计算出G_r，然后算出N_um。则计算出表面传热系数为

式中 λ₁——炉气的热导率；

d——定型尺寸，棒材外径。

由式（9-34）可以计算出不同定型尺寸d对应的表面传热系数。(www.xing528.com)

辐射换热是第二类边界条件，它包括两部分：①炉墙与钢棒的辐射换热；②炉气与钢棒的辐射换热。为了计算方便，认为炉墙、炉气温度与炉温相同。

炉气与棒材的辐射换热为

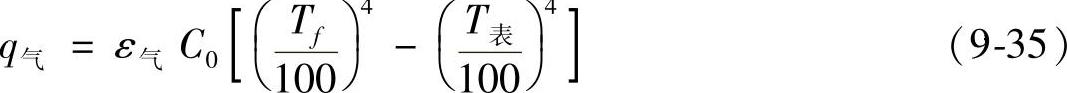
式中 ε_气——炉气的黑度系数；

C₀——黑体的辐射系数，C₀＝5.6W/（m²·K^－4）。

炉墙与棒材的辐射换热为

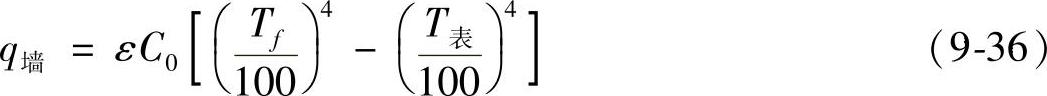
式中 ε_s、ε_g——分别为炉墙和棒材的黑度系数，查得ε_s＝0.85、ε_g＝0.75；

φ_gs——炉墙对钢棒的角系数；

φ_gs——棒材表面积/炉墙的有效表面积。

4.差分方程的计算机求解

（1）显式解法 用显式差分方程计算时，每个节点温度可单独求解。因此，可根据已知的初始温度求解1Δτ时刻的各节点温度，然后由1Δτ时刻各节点的温度求得2Δτ时刻各节点温度值，如此逐层计算，直至求得所需时间的各节点温度为止。计算程序框图如图9-10所示，图中各变量说明见表9-2。

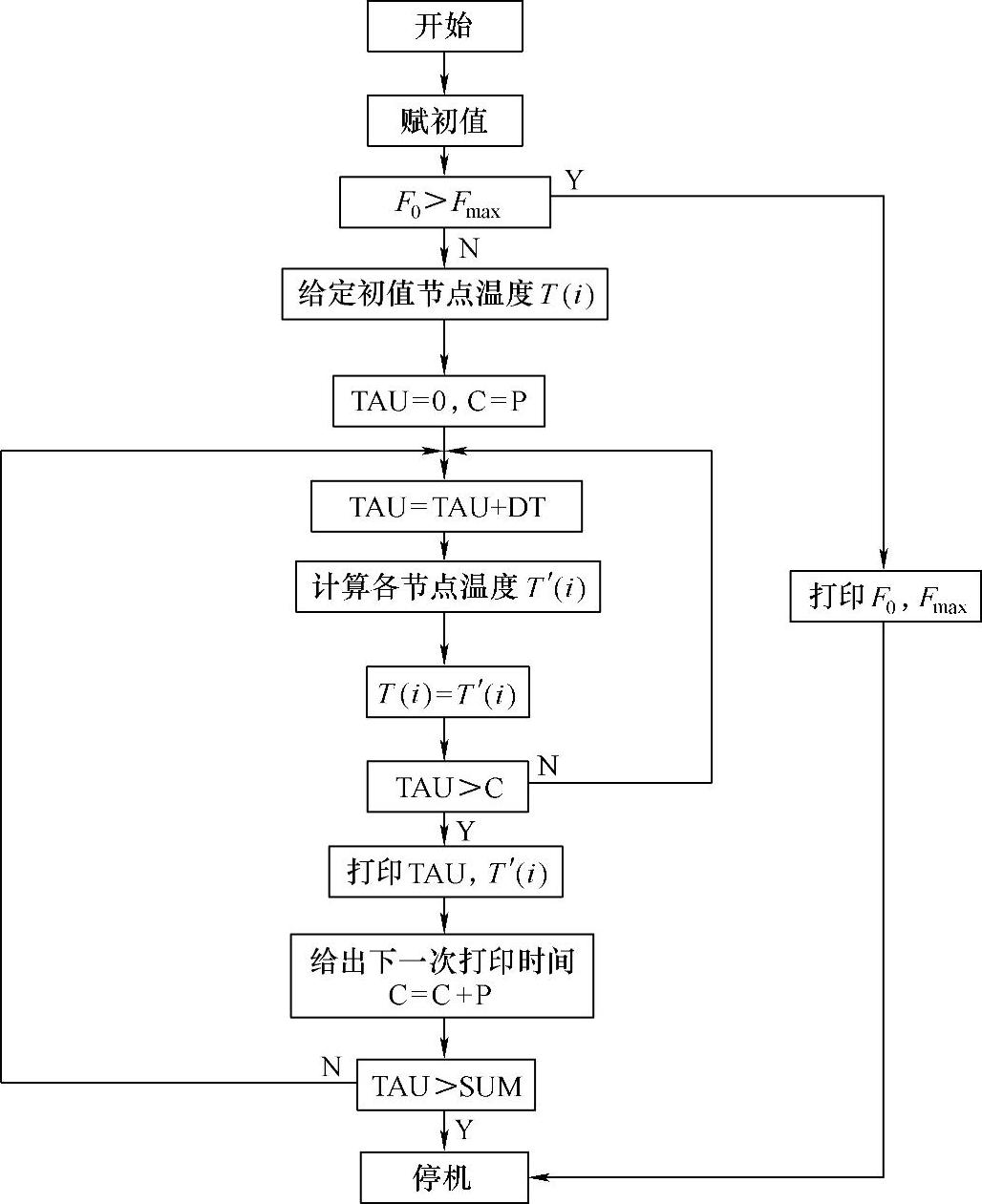
图9-10 显式差分方程求解的计算程序框图

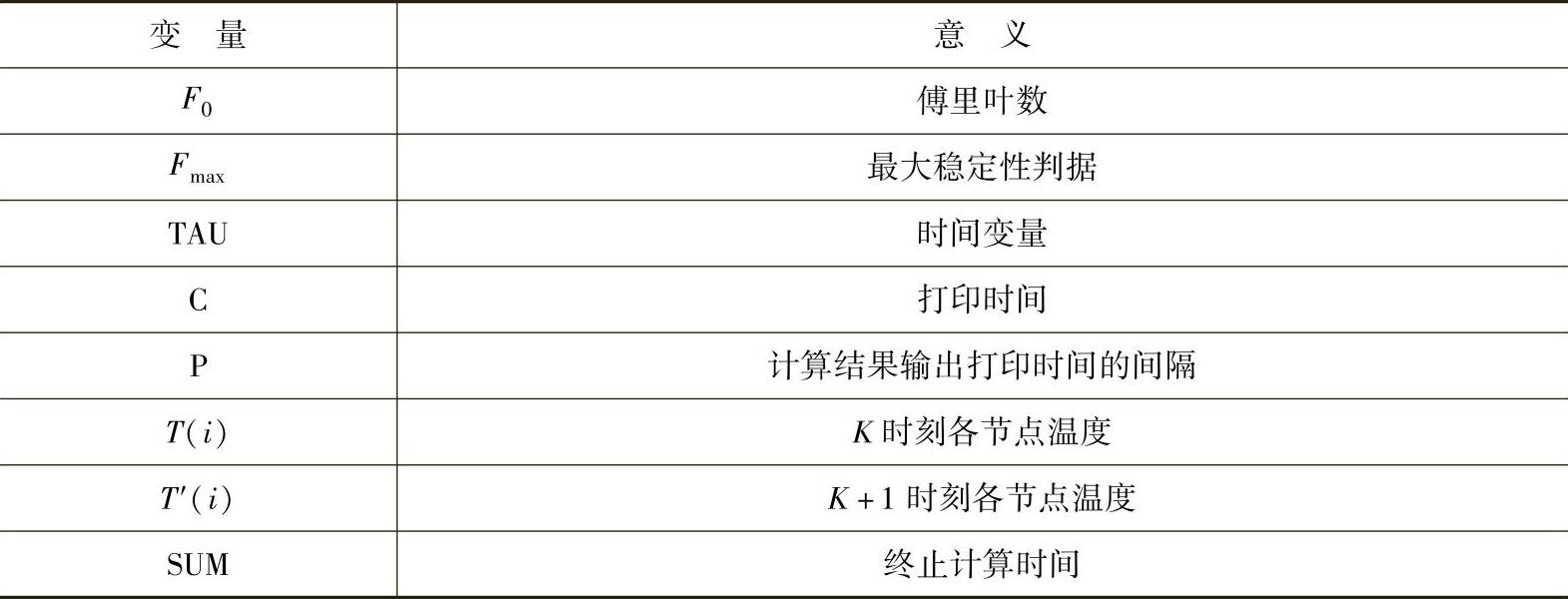
表9-2 图9-10中各变量说明

在用显式差分方程作数值运算时，一个非常重要的问题是它的稳定性，具体讲就是计算时差分方程中F₀值的选取。如选取不当，所得到的解将不稳定，而不稳定的解是没有意义的。F₀值的选取必须满足一定的条件，这个条件称为稳定性判据。研究表明，显式差分方程的稳定性判据是：F₀值的大小应满足方程T^k_i的系数不为负值。对于棒材温度场沿径向的一维传热问题，根据差分方程式9-31，只要F₀≤0.25就能保证所有差分方程式的系数不为负值，满足稳定性判据，即F₀≤0.25或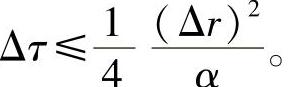

（2）隐式解法 隐式解法的优点是对于任何Δt（即选用任何的F₀）都是稳定的，但其代价是每一步上都有较大的截断误差。因此，精确度稍受损害，其精确度决定于Δt的选取。Δt越小，计算就越精确。所以，为了得到较好的精确度，Δt必须适当小些，而且每推进一个时间步长所需要的工作量比更为简单的显式公式要多。

隐式差分格式包括完全隐式差分格式、六点差分格式及一般差分格式，它与显式差分格式的基本区别是其代数方程组必须联立求解。联立求解方程组的方法有直接解法，即高斯（Gauss）法，还有迭代法，包括简单迭代法、高斯-塞德尔（Gauss-Seidel）迭代法，具体的解法在有关参考文献中有详尽的介绍。而针对一维不稳定导热问题还有更简捷的方法，称为“追赶法”。

对于前述的棒材一维导热问题，其隐式差分方程如下：

中心节点i＝0的差分方程式为

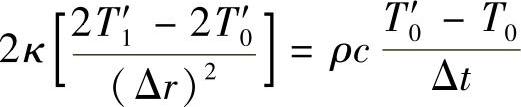
图9-10 显式差分方程求解的计算程序框图

即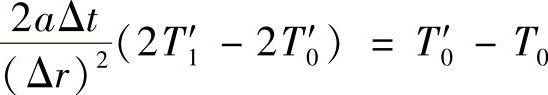

其中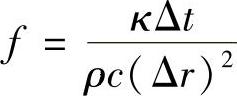

内部节点i＝1～n－1的隐式差分方程式为

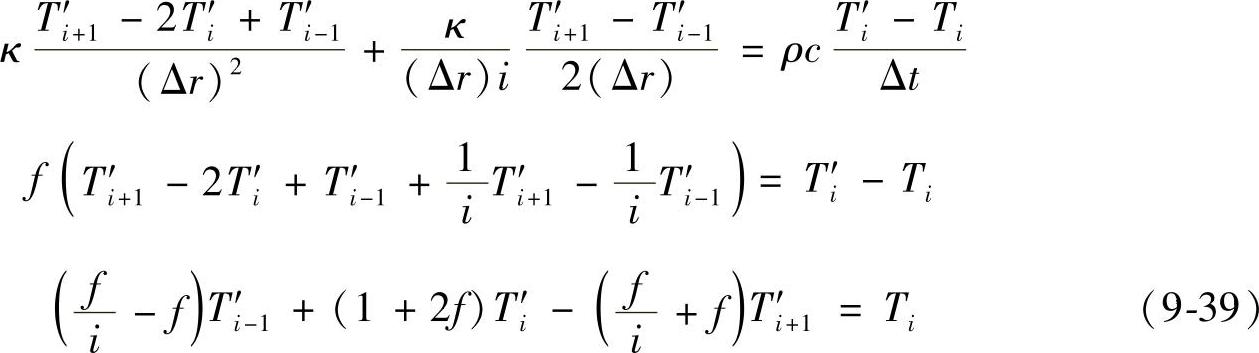
外边界节点i＝n的隐式差分方程式为

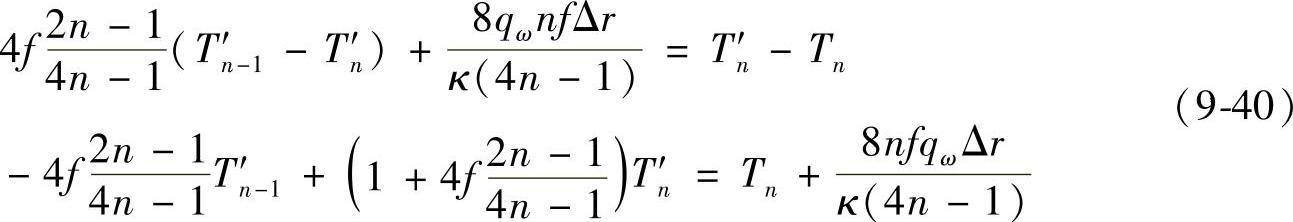
将式（9-40）写为矩阵的形式如下

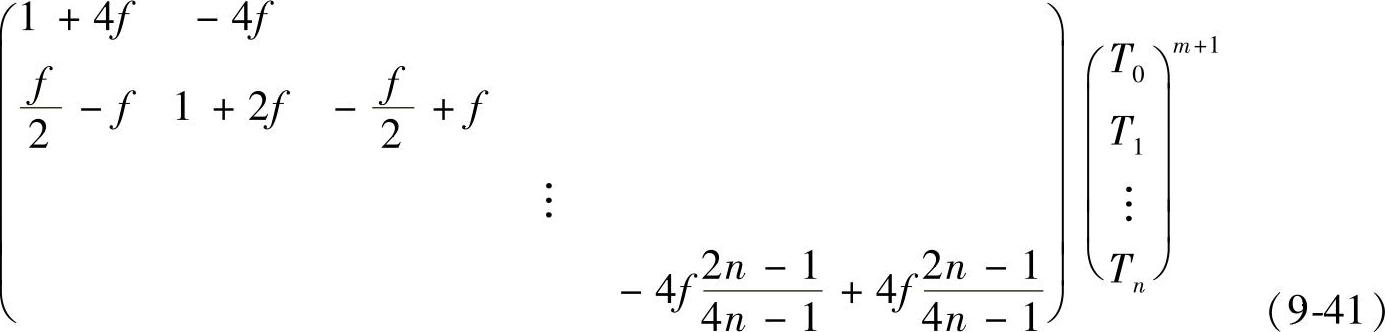
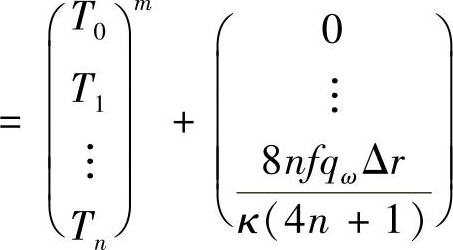
为了叙述方便，将方程组[式（9-41）]理解为更一般的形式，即

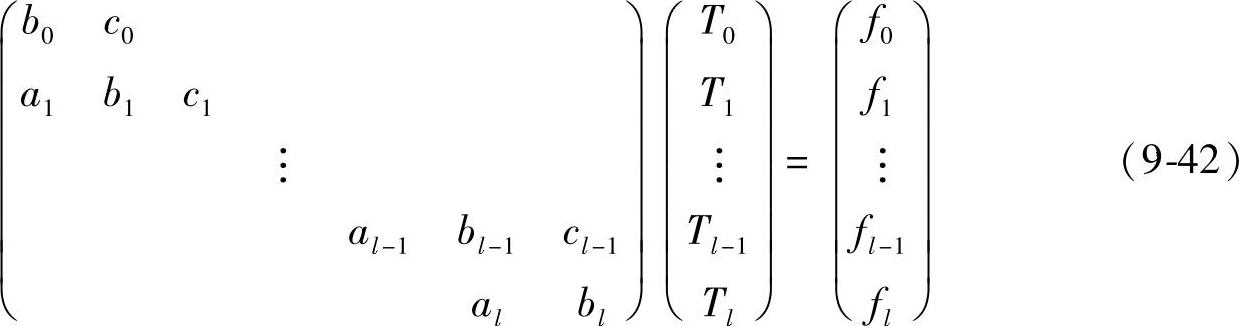
方程组[式（9-42）]可写成如下展开形式

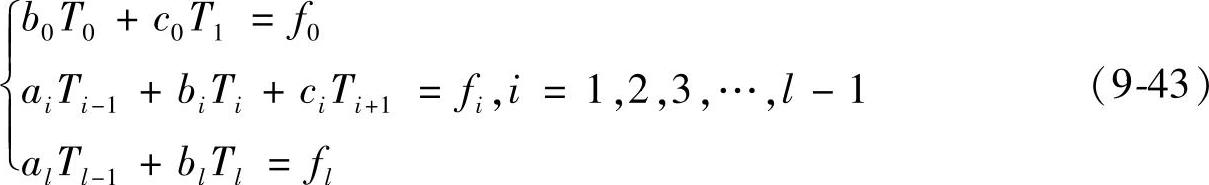
为了求解方程组[式（9-43）]，先将第一个方程改写为

式（9-44）是用T₁表示T₀的公式，简写成为

T₀＝U₀T₁＋V₀（9-45）

其中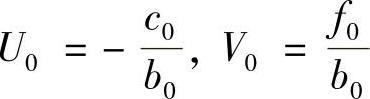

将式（9-44）代入式（9-43）中的第二个方程

a₁T₀＋b₁T₁＋c₁T₂＝f₁

得a₁（U₀T₁＋V₀）＋b₁T₁＋c₁T₂＝f₁从而又可以解出T₁，得到用T₂表示T₁的公式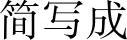

c₁f₁^－a1V0T₁＝－T₂＋（9-46）

a₁U₀＋b₁a₁U₀＋b₀

T₁＝U₁T₂＋V₁

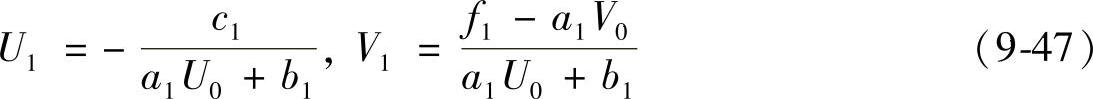
则有了用T_i表示T_i－1的公式为

T_i－1＝Ui_－1^Ti＋Vi－1将式（9-47）代入式（9-43）的第i个方程，得

a_i^Ti－1＋biTi＋ciTi＋1＝f_i

则有a_i（U_i－1T_i＋V_i－1）＋b_iT_i＋c_iT_i＋1＝f_i

即（a_iU_i－1＋b_i）T_i＋c_i^Ti＋1＝f_i－a_iV_i－1由上式得到了用T_i＋1表示T_i的表达式为T_i＝U_iT_i＋1＋V_i

c_if_i^－aiVi－1Ui＝－，Vi＝（9-48）

a_iU_i－1＋b_ia_iU_i－1^＋bi

依此类推，最后，当i＝l－1时，得

T_l－1＝Ul_－1^Tl＋Vl－1（9-49）

式（9-49）与式（9-43）中的最后一个方程a_lT_l－1＋b_lT_l＝f_l联立构成二元一次方程组，由此可得

利用已解得的T_l，代入式（9-49）就可求得T_l－1，再反复利用式（9-47），在已知T_l的情况下，可求得T_l－1（i＝l－1，l－2，…1）。这样依次可求得方程中T_l－1，T_l－2，…，T1之值，从而得到方程组（9-43）的解。

综上所述，式（9-43）的求解过程可分为两大步：第一步依次序决定U₁、V₁，U₂、V2，…，Ul、Vl，称为顺追赶；第二步逆次序依次决定T_l，T_l－1，…，T₁，称为逆追赶。整个求解过程称为追赶法。

在上述顺追赶求解系数U_i、V_i（i＝1，2，…，l－1）及T_l时，要遇到除法运算。因此，在运用追赶法时，除了要求B_i≠0，还必须要求在求解U_i、V_i、T_l时分母项不应为零。

对于一维不稳定导热的隐式格式，它的系数矩阵式[式（9-41）]中第一项的另一特点是主对角线上元素的绝对值与同一行中其他元素绝对值之和相比在数量上占有优势，这个条件称为矩阵具有主对角线优势。这种主对角线优势的矩阵不仅能保证解的唯一性，而且在计算U_i、V_i及求解T_l时不会出现分母为零的情况。根据追赶法的思路写出程序框图，如图9-11所示。

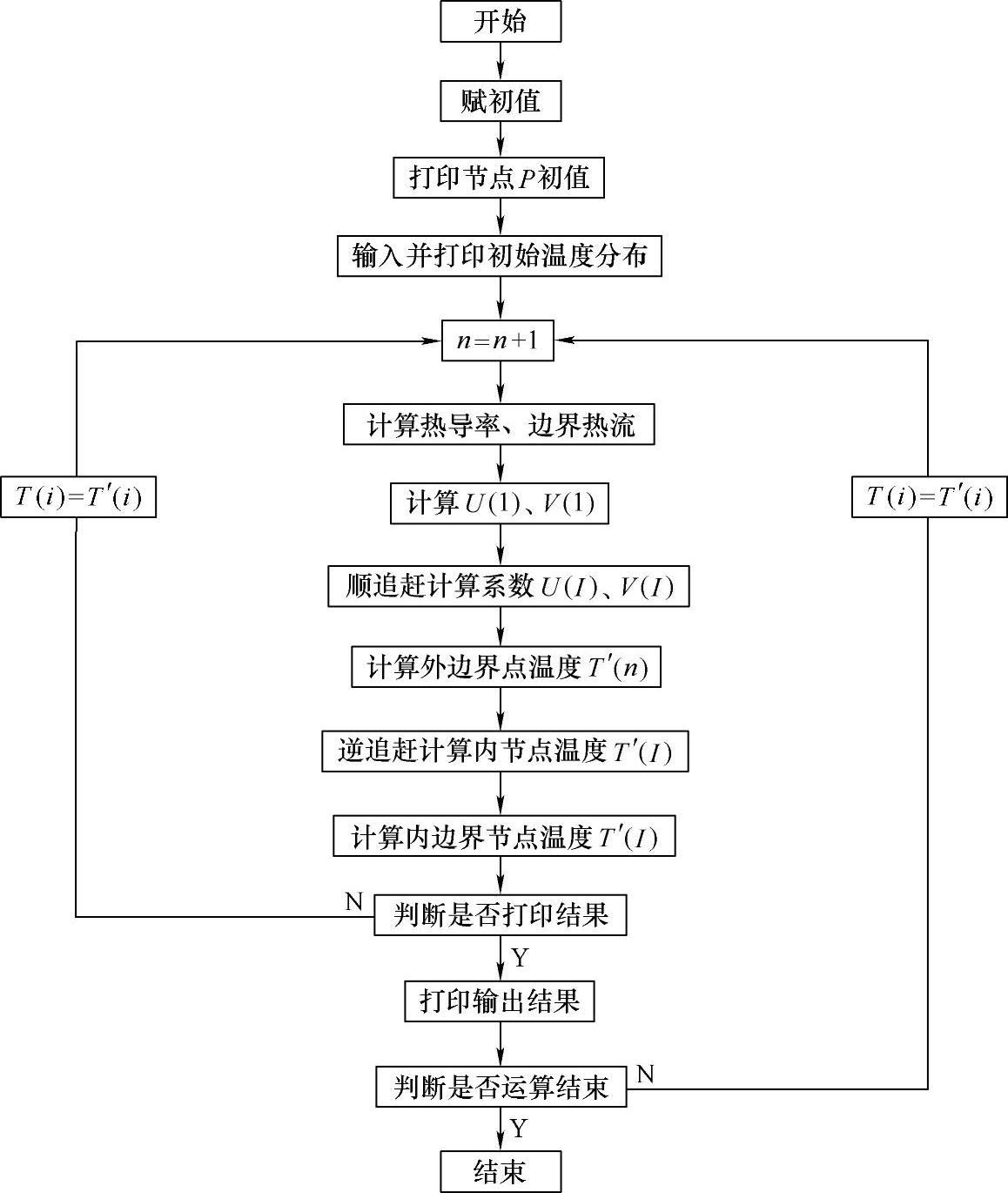
图9-11 追赶法求解温度场计算程序框图

5.典型退火工艺的计算举例

（1）轴承钢GCr15、GCr9球化退火工艺计算 GCr15、GCr9等轴承钢棒材的球化退火要求得到细小均匀的球化组织，为了达到球化组织级别的要求，退火温度和时间即送料速度均应严格控制。

为了获得良好的球化组织，采用两个阶段保温。根据GCr15、GCr9钢的临界点，第一阶段保温温度选择在810℃较为合适。如果温度太低，网状碳化物不易溶解，在随后冷却过程中不易得到粒状碳化物；温度太高则碳化物溶解过多，未溶的碳化物颗粒太小，奥氏体成分均匀，在随后冷却过程中缺少未溶的颗粒，也不易得到符合要求的粒状碳化物组织。为了得到奥氏体和未溶碳化物组织，加热后要保温，不同尺寸规格的棒材保温时间也不同，要根据不同规格确定合理的加热时间。随后冷却到第二阶段保温，此时未溶的碳化物颗粒不断长大，到A₁以下得到铁素体和颗粒状碳化物组织。因此，第二阶段保温定在725℃为宜，保温时间也根据不同的尺寸规格而不相同。在保温后的冷却过程中，冷速也要适当地控制，以达到组织转变要求。所以，由810℃到725℃的冷速应小于25℃/h，而由725℃到650℃的冷速应小于30℃/h，由650℃到550℃的冷速应在50℃/h左右。根据上述工艺要求，针对不同规格棒材分别计算了温度场随时间的变化，辅助设计出钢棒的球化退火工艺。图9-12所示为GCr15钢ϕ85mm棒材的热处理工艺曲线，其中虚线为炉温，实线为棒材中心的温度。

（2）合金工具钢4CrW2Si、CrW5等钢的低温退火 合金工具钢棒材轧后需进行去应力处理，以改善组织、降低硬度。退火可以采用Ac₁稍上或稍下的温度加热，在Ac₁稍下加热主要依靠回复再结晶来达到去除应力及降低硬度的目的；在Ac₁稍上加热可通过相变重结晶达到目的，其效果较Ac₁以下为好。所以，加热温度选择在Ac₁稍上的780℃保温随后冷却，780～550℃之间的冷速应在50～60℃/h，550℃出炉。保温时间根据棒材的直径大小不同各异，同时工艺要满足热处理炉子长度的要求。根据上述退火的要求，对不同直径的钢棒进行了温度场计算，辅助设计了4CrW2Si钢的低温退火工艺，如图9-13所示。

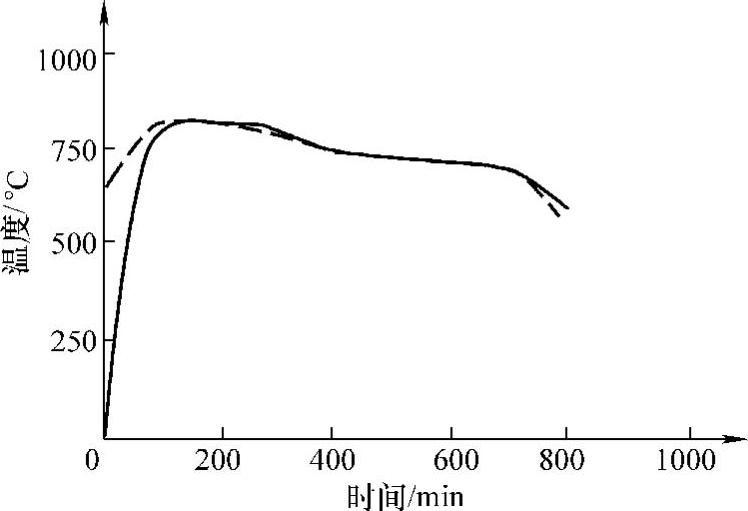
图9-12 GCr15钢ϕ85mm棒材的退火工艺曲线

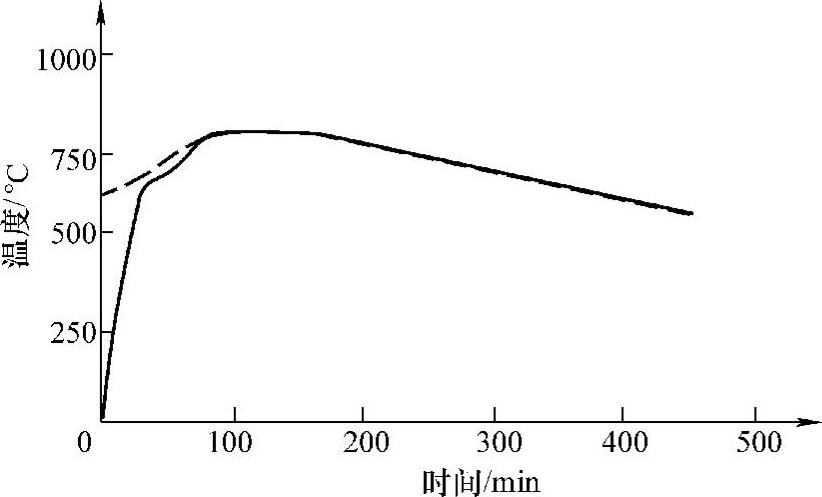
图9-13 4CrW2Si钢ϕ50mm棒材的低温退火工艺