避免误判：切变机制的注意事项

21世纪以来，刘宗昌等人通过深入实验观察分析，从热力学、晶体学、组织学、表面浮凸等多方面逐一对切变机制进行了实践检验和理论检验，从多角度、多方面分析了马氏体的切变机制的误区^[3，4，15]。

1.切变过程缺乏热力学可能性

使晶体发生切变需要施加切应力τ，τ＝Gβ，其中G为切变弹性模量，β为切应变。

切变耗能Ns用下式计算^[15]

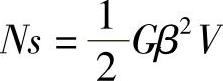
式中，V是马氏体的摩尔体积。根据K-S模型，当γ-Fe→α马氏体（w_C＝0）时，第一切变角为19°28′，折合0.34rad。将相关数值代入上式，计算出切变消耗的功为N_1q＝35×10³J/mol，此即按照K-S模型第一切变需要的切变能量。K-S模型的第二切变是切变10°32′，计算需要切变能量N_2q＝9.9×10³J/mol。将两次切变消耗的功相加，即切变总能量N_k＝N_1q＋N_2q＝44.9×10³J/mol。

西山切变模型只进行第一切变，并且与K-S模型的第一切变相同，因此需切变能量N_x＝N_1q＝35×10³J/mol。

1949年提出了G-T模型，按照表面浮凸效应测得平均切变位移为10.75°，应当耗能N_G1＝0.5Gβ²V＝10.8×10³J/mol。G-T模型的第二切变是在马氏体（112）M上切变，切变角θ＝12°～13°，则第二切变耗能N_G2＝14.5×10³J/mol。两次切变共需切变能N_G＝N_G1＋N_G2＝25.3×10³J/mol。

上述各切变模型在完成1～2次切变后，显然消耗了极大的能量。遗憾的是切变后均没有得到实际的马氏体晶格，还需进行晶格参数调整，这实际上还需要原子再移动、再耗能，在上述计算的切变能量基础上还需要追加晶格参数调整的能量。这些切变模型只是考虑将面心立方变成体心结构（并非体心立方），或产生孪晶、位错亚结构，而没有考虑能量的来源和相变阻力的大小，没有考虑相变驱动力是否能够满足这些切变过程，忽视了热力学可能性。

纯铁马氏体相变的临界驱动力约为1.18×10³J/mol，w_C＝0.4％～1.2％的Fe_- C合金的相变驱动力为1.337～1.714×10³J/mol^[1]。

将切变能耗与相变驱动力比较，发现马氏体相变驱动力远远不能支持切变过程的进行。可见切变过程不符合省能原则，不可能发生，这是一大误区。而且切变过程并没有得到符合实际的真正的马氏体晶格参数，却已消耗了大量的能量。根据自然事物演化的原则，旧相到新相的转变遵循省能原则，系统自组织功能不会选择切变方式，而要选择省能途径。

2.马氏体相变晶体学切变模型与实际不符

自20世纪30年代提出第一个马氏体切变模型到70年代提出八个切变模型，如K-S模型（1930）、西山模型（1934）、G-T模型（1949）、表象学假说（1953—1954）、K-N-V模型（1961）、B-B双切变模型（1964）、ЛЫСаК模型（1966）、藤田模型（1976）。这些模型的致命缺点是与实际基本上不符。

Γ.Β.库尔久莫夫和G.萨克斯（Sacks）于1930年首先测得w_C＝1.4％的钢中马氏体与母相奥氏体保持K-S关系。并且以此设计了K-S切变晶体学模型。1934年，西山测得（34～37）％Ni-Fe合金马氏体相变时存在西山关系，设计了西山切变模型，其第一切变与K-S模型相同，但不进行第二切变，并调整面间距等参数，使其与实际马氏体的晶格参数相一致。

以上两个模型都使奥氏体变成了体心结构，并满足其所测的位向关系。但按照这些模型，惯习面应为｛111｝_γ，而实际上钢中马氏体的惯习面为｛557｝_γ、｛225｝_γ、｛259｝_γ；该成分的Fe-Ni合金马氏体的惯习面也是｛259｝_γ，惯习面与实际不符。此外，这些模型均不能产生高密度位错、精细孪晶和微细层错等亚结构。经过1～2次切变后，实际上只是得到体心结构，但是其晶格参数并非实际的马氏体晶格，也即切变后没有得到实际的马氏体晶体，还要通过原子的再移动、再耗能才能得到实际的马氏体晶体。

A.B.Greninger，A.R.Troiano于1949年测定了Fe-22％Ni-0.8C％合金中的马氏体位向，发现了G-T关系，并且设计了G-T切变模型。G-T模型经两次切变后并没有完全达到实际晶体要求，为了满足晶体学要求，仍需做晶格参数的调整。它与该合金的惯习面不符，也与w_C≤1.4％钢中马氏体的惯习面不符。虽然预示马氏体中存在位错，但是不能解释马氏体中复杂的缠结位错形态和层错亚结构的成因。

20世纪50年代提出的两个马氏体相变的表象学假说，其一称为“W-L-R理论”，另一个称为“B-M理论”。该学说将Bain模型和切变模型组合起来，并以矩阵式F＝RBS描述。现研究表明表面浮凸是新旧相的比容差所致，简单切变不能获得真正的马氏体晶格。因此，将形状应变（表面浮凸）F用RBS三因素的组合来描述，这个计算式的物理模型不正确，因而其计算结果与绝大多数合金和钢的相变实际不相符合是理所当然的。

到了20世纪70年代，科学工作者不断提出或改进切变模型，如Bogers-Bur-gers双切变模型、范性协作模型等。除了Bain应变模型外，其余均为切变模型或以切变模型为基础的改进型模型。遗憾的是，所有切变模型均不能与实际完全符合，尤其是对于钢中的马氏体相变基本上不符合；所有切变模型均不能解释马氏体组织形貌和高密度的缠结位错、精细孪晶、层错等亚结构的成因。数十年来切变模型的所谓“改进”成效甚微，按照科学技术哲学理论^[17]，与实际不符的假说或未被试验证实的观点不能称为理论，实践是检验真理的唯一标准，从这个角度讲切变机制是不成功的。

3.切变机制缺乏试验依据

20世纪初发现马氏体相变的表面浮凸现象，认为是切变造成的，并且将表面浮凸形貌描绘为N形，作为马氏体相变切变机制的主要实验依据。对表面浮凸的错误认识是导致切变机制误区的根源。

到目前为止，已经发现在珠光体、贝氏体、马氏体、魏氏组织中均存在表面浮凸现象，而且浮凸形状普遍为帐篷形（∧）。浮凸实际上是试样表面的过冷奥氏体转变产物的一种普遍表征^{[9，18，19]}。

试验发现，马氏体表面的浮凸与珠光体、魏氏组织、贝氏体等转变产物的浮凸相比没有特殊之处，所有板条状马氏体的表面浮凸均为帐篷形（∧），帐篷形浮凸不具备切变特征^[20]。研究发现，Fe-Ni-C合金｛259｝_f形片状马氏体的表面浮凸也为帐篷形（∧）。

图5-39所示为20Cr13钢板条状马氏体的表面浮凸观测结果，图中下部为马氏体的浮凸形貌，上部为对应的浮凸高度。图5-40所示为Fe-15％Ni-0.6％C合金的片状马氏体表面浮凸。各种浮凸的形状均为帐篷形（∧），这与近年来研究者们的观测结果是一致的。应用STM、AFM精确测定浮凸尺寸和形貌，发现浮凸均具有平面特征，将马氏体表面浮凸与其他相变产物的浮凸相比没有发现特别之处。(www.xing528.com)

试样表面层的奥氏体转变与内部的相变环境不同，转变有所区别。试验表明：表面马氏体是在奥氏体晶界形核，在试样表面上长大；而试样内部在晶界上形成的马氏体不可能同时与两侧的奥氏体晶粒保持共格连接，与空气接触（或真空）的外表面更不存在共格关系，则马氏体片难以以“切变共格”方式形核长大。

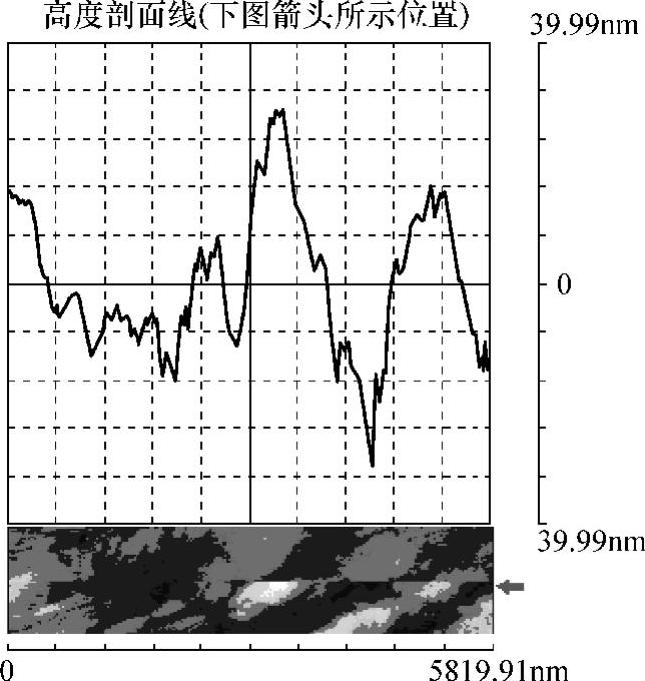
图5-39 20Cr13钢的板条状马氏体浮凸（STM）

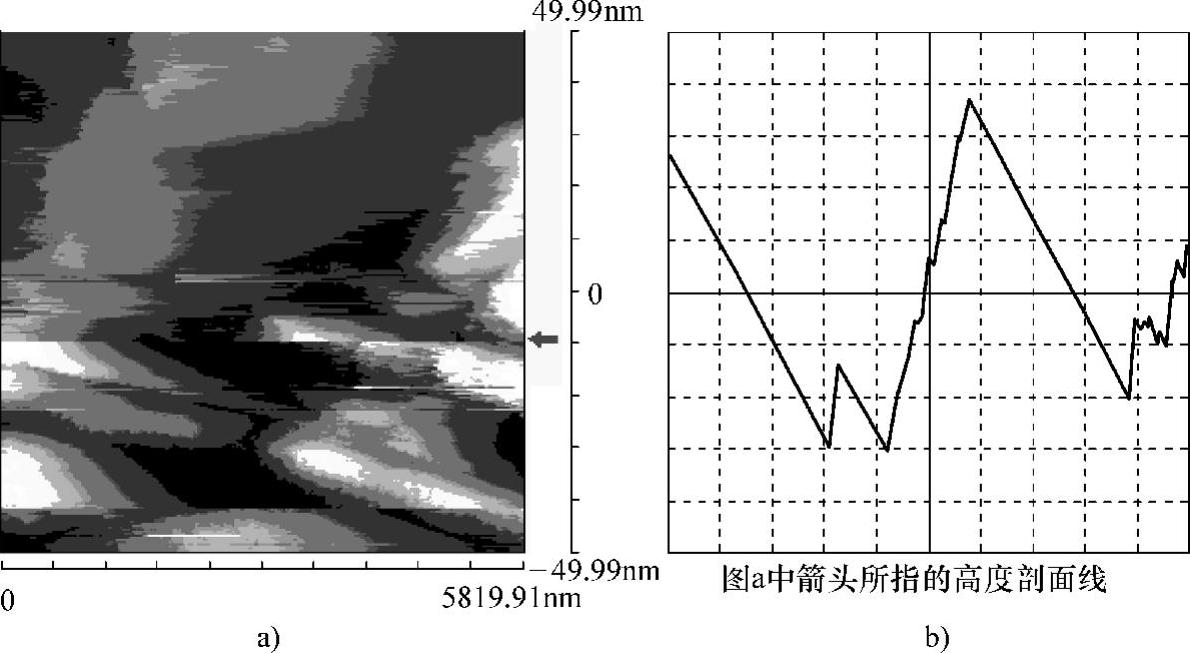
图5-40 Fe-15％Ni-0.6％C合金的片状马氏体浮凸（STM）

a）浮凸形貌 b）浮凸高度剖面线

当试样表面上的过冷奥氏体转变为马氏体时，表面浮凸主要是由于各相的比体积不同，马氏体片形成有先后，相变体积不均匀膨胀造成的。

当试样表面上的奥氏体转变为贝氏体或马氏体时，也同样发生不均匀的体积膨胀，而且形成复杂的表面畸变应力，从而引起表面畸变。新相形成有先后，则凸出于试样表面的尺寸不等，因而产生与组织形貌相适应的浮雕，即为浮凸。

20世纪前半叶，扫描隧道显微镜（STM）、原子力显微镜（AFM）尚未问世，只能使用光学显微镜观察表面浮凸形貌，难以测定浮凸的高度。图5-41所示为将高碳钢高温加热后淬火，然后将试样垂直的两面抛光、浸蚀，进行金相观察，得到马氏体片与表面相交的形貌及描绘为N形的示意图^[1，21]。为了清晰地观察浮凸形貌，本书作者利用计算机画图工具沿着试样表面画了一条水平线。显而易见，形成马氏体片的部位只有鼓出，没有下陷，说明是体积膨胀的结果。浮凸形貌是帐篷形（∧），并非N形，没有切变特征。如是N形切变，则从表面的鼓出量和下陷量应当相等（图5-41b）。应当指出，原作者的试验观察是成功的，但是将此图形处理为N形（图5-41b、图5-41c）是不正确的，是对试验数据的不实事求是的处理。

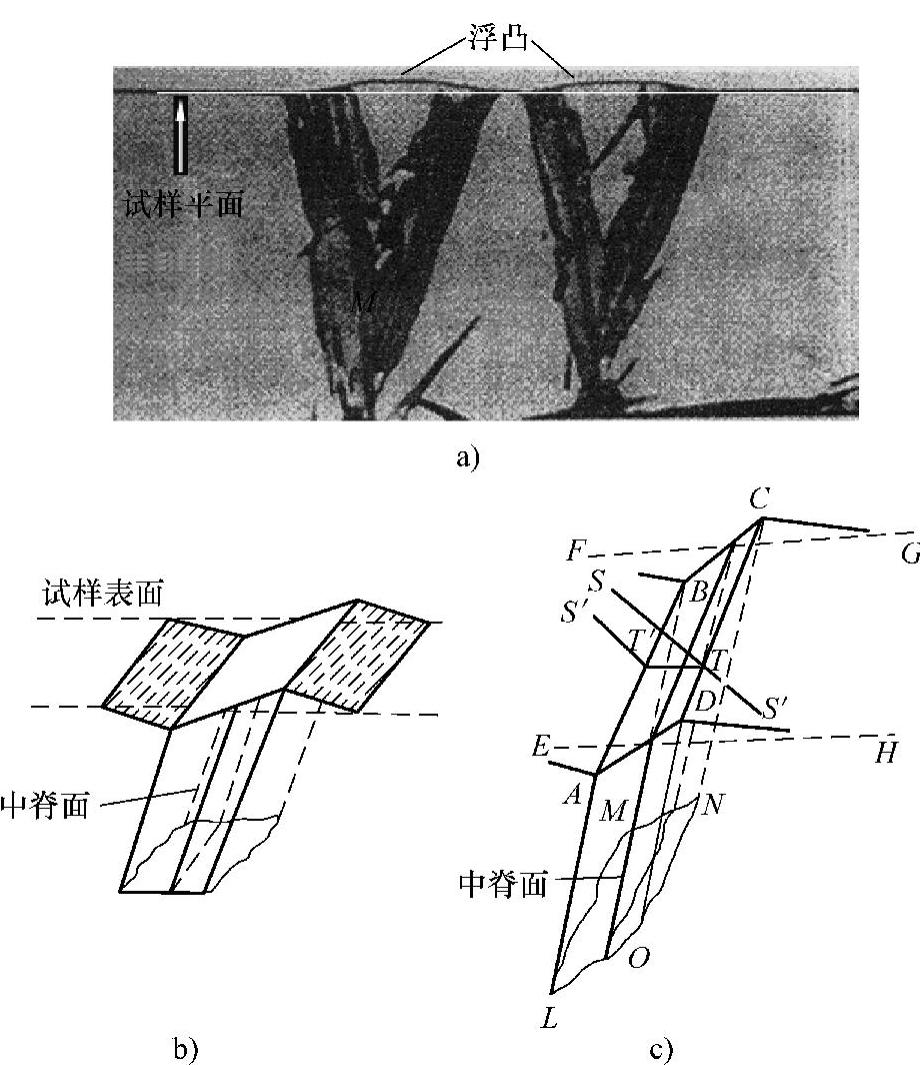
图5-41 高碳马氏体的表面浮凸（OM）及示意图

由于认为切变导致N形浮凸，因此在试样表面刻一条划痕STS′，马氏体转变后，该划痕变成折线S′T′TS′，折线应当连续不间断^[1]。应当指出，图5-41b及图5-41c所示的示意图在书刊文献中找不到试验支持。

为了检验该示意图的正确性，特取Fe-Ni-C合金试样并抛光（刻意留有划痕），然后进行光亮的真空热处理，不对试样进行任何表面处理，即不浸蚀，随即用扫描电镜直接进行观察，发现了马氏体表面浮雕（浮凸），马氏体表面浮凸的形貌与马氏体片的组织形貌相对应，为条片状，如图5-42所示。由图中可见，试样表面上的原有划痕仍然清晰可见，从箭头所指处可见划痕变弯曲，箭头1、2、3所指位置划痕变成曲线，箭头4、5、6所指位置划痕有间断、不连续现象，说明由于条片状表面马氏体的形成而使直线划痕变成了曲线，且断裂、不连续。

图5-42 Fe-15％Ni-0.6％C合金马氏体表面浮凸的形貌及划痕的变化（SEM）

表象学学说指出：表面形成马氏体后刻划的直线STS′变成折线ST′TS′，并在相界面处保持连续不间断。说明在马氏体和奥氏体共格的惯习面上没有发生转动和畸变，认为惯习面是无畸变、不转动的不变平面，这是不符合实际的分析。试验证明，划痕STS′线变成了弯曲、断裂的曲线，因此所谓的“不变平面应变”实际上是不存在的。

图5-43是又一幅扫描电镜照片，图a中的F划痕和图b中的C划痕是两条较长的划痕。在表面马氏体形成后，图a中的F划痕变成了曲线，并且有多处断裂；而图b中的C划痕虽然很长，但是跨越许多马氏体片后仍然基本上保持一条直线。图b中的B划痕变成了一条弧线，图a中的E划痕、图b中的A划痕均发生断裂现象。

图5-43 Fe-15％Ni-0.6％C合金马氏体表面浮凸和划痕的变化（SEM）

扫描电镜观察表明，直线划痕由于马氏体表面浮凸的形成而变化多端，成为曲线，出现间断、不连续或基本上不变等现象。这说明马氏体表面浮凸是表面马氏体体积膨胀及不均匀应变的结果，并非切变所致，也不呈N形，而是帐篷形。N形浮凸缺乏实验依据，是马氏体切变机制误区的策源地。

综上所述，切变机制不能满足相变热力学条件，所有晶体学切变模型均不能与实际完全符合，表面浮凸是试样表面的过冷奥氏体转变的一种普遍现象，表面浮凸呈帐篷形（∧），不具备切变特征，N形浮凸缺乏实验依据等，故切变机制是不成熟的学说。