相变动力学方程简介

1.Johnson-Mehl方程

根据上述长大速度和形核率，可以计算出新相的体积分数（φ_实）与时间（t）的变化关系，即Johnson-Mehl方程^[2]

式（4-14）应用时有四个约束条件：任意形核、形核率N·为常数、长大速度G为常数、时间t很小。将式（4-14）绘出图形，其动力学曲线呈S形，等温转变图呈C形。

2.Avrami方程

上述Johnson-Mehl方程与实际的相变过程有差距。实际上形核率和长大速度均不为常数，故改用Avrami提出的经验方程式^[2]

φ＝1－exp（－btⁿ） （4-15）

式中，b和n取决于形核率和长大速度。如果母相晶粒不太小，晶界形核很快饱和。假设晶核长大速度G为常数，形核位置饱和后，其转变过程仅由长大过程控制，这时因形核率已经降低到零。则Avrami方程式分别为(www.xing528.com)

界面形核时：φ＝1－exp（－2AGt）

晶棱形核时：φ＝1－exp（－πLG²t²）

晶隅形核时：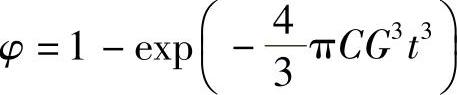

式中，A、L、C分别为单位体积中的界面面积，晶棱长度、界隅数。若母相晶粒直径为D，则A＝3.35Dd^－1、L＝8.5D^－2、C＝12D^－3。

Johnson-Mehl方程和Avrami方程仅仅适用于扩散型相变，因此对于奥氏体的形成和珠光体转变，上述两个方程反映了一定的规律性。而对于贝氏体相变和无扩散的马氏体相变，其相变动力学是不能应用的。