形核率与能量分配定律的关系及其在相变动力学中的应用

形核率是经典的相变动力学讨论的中心问题之一。形核率是单位时间、单位体积母相中形成的新相晶核的数目，其表达式为

式中，C^∗为母相中临界尺寸的新相核胚的浓度（个/单位体积）；f为临界核胚的成核频率（次数/单位时间）。

C^∗、f两值确定后即可得出形核率的完整的数学表达式。

1.临界核胚浓度C^∗

要想确定C^∗值，首先要搞清“可供形核地点”的问题。核胚可能以任意一个阵点作为基础而形成，因此晶体阵点就是可供形核的地点。单位体积内可供形核的地点数目C₀就是阵点密度（个/单位体积）。形成临界核胚大小n^∗时，每个原子所需的能量上涨值为

按照Maxwell-Boltzman能量分配定律，任何一个独立振子其振动能量处于常态（ΔU或高于ΔU）以上的几率为

n^∗个原子的能量同时上涨ΔU（或高于ΔU）的几率为

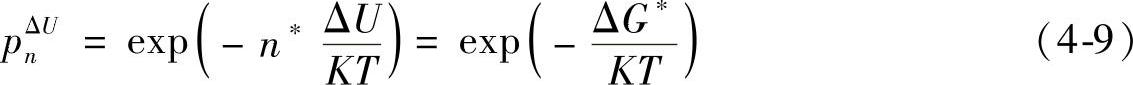
则临界核胚浓度C^∗为

2.临界核胚成核频率f(www.xing528.com)

一个临界核胚当其周围母相原子由于热振动而进入该核胚时，则成为n^∗＋1的新原子团，从而超过了临界晶核的大小，即获得了稳定生长的能力。

n^∗核胚在单位时间内接受紧邻原子振动碰撞的次数为f₀，即

f₀＝SV₀p （4-11）

式中，S为紧邻原子数；V₀为原子振动频率；p为在进入核胚n^∗方向上的震动分量（分数）。

按照Maxwell-Boltzman能量分配定律，在f₀次碰撞中，有多少次可以进入核胚，并成为n^∗核胚上的原子，则可计算临界核胚的成核频率f。设母相原子跨过核胚界面进入新相核胚所需的能量上涨值为Q，则f为

式中，Q值接近母相原子的自扩散激活能。

依据上述计算，可以得出晶核的均匀形核率为

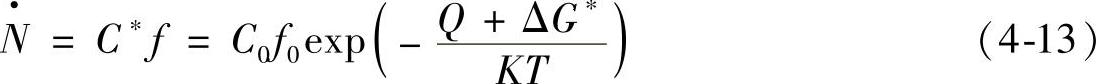
在上式的exp项中，温度T的下降引起Q值和ΔG^∗值向相反的方向变化。随着T的下降，ΔG^∗/KT值升高。而对于Q项，由于晶格能垒几乎不随着温度变化而变化，所以温度下降，Q/KT值上升。这样，就导致N·-T曲线上出现极大值，如图4-19所示。

实际上，晶核的形成是一个动态过程。有些临界核胚得到了原子而成为晶核，这使得临界核胚的浓度降低。同时，由于热激活，随机涨落又不断形成新的核胚，当平衡时出现稳定状态。

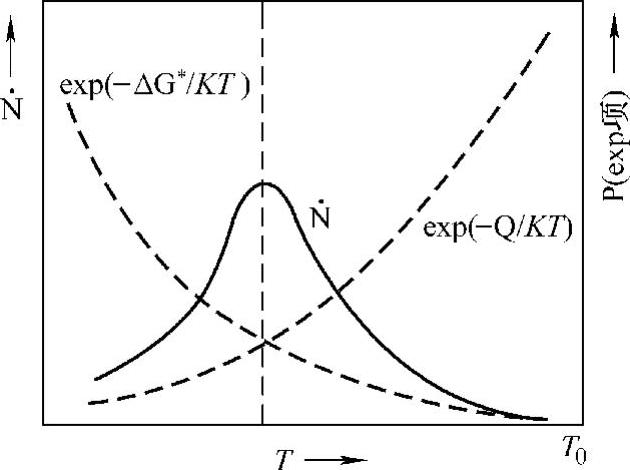
图4-19 形核率与温度的关系曲线