金属半固态非枝晶组织凝固形成机理优化

在半固态金属的浆料制备过程中，一边进行液体的搅拌（剪切），一边进行着金属的结晶，在熔体中生成一部分固相。液相区液体的流动，将改变凝固界面前沿液体的温度场和浓度场，从而对凝固组织的形态产生影响。以低熔点类透明有机物为例，可观察到枝晶定向凝固，若无对流，呈正常的、发达的树枝晶，如图5-7所示^[5]。若有平行于凝固界面的流动存在、流速较小时，将发生枝晶间距的增大，并且一次枝晶的成长方向偏向来流方向几度，如图5-7上部所示。同时，来流方向的二次枝晶成长较好，背流侧的二次枝晶几乎不生长。一次枝晶偏向来流的原因是一次枝晶先端的液体内温度分布及成分分布变得非对称的缘故，即结晶生长形态会发生改变。

当流速增大到一定值时，原来的主轴晶将无法生长，而在背流处形成新的主轴晶，并与原来的主轴晶竞相生长，获得一种特殊的凝固组织，即穗状晶。

当流体流速与凝固界面垂直时，可能产生比较严重的宏观偏析。强烈的紊流可能冲刷新形成的枝晶臂而造成晶粒繁殖，并对细化等轴晶有一定的帮助。

由大量的试验结果可知，经过激烈搅拌后的金属半固态浆料（Semi-solid slurry）的凝固组织与未搅拌的半固态浆料的凝固组织之间有明显的区别。后者的淬火组织特点是先析出粗大的树枝晶组织，并互相搭接成骨架状结构，如图5-8所示。相反，前者的淬火组织特点（见图5-9）是：淬火前已经凝固的非枝晶初生晶粒均匀地悬浮在母液中，这些晶粒大多呈球状、椭球状或花瓣状，大部分初生晶粒之间并无搭接，但也有部分初生晶粒相互聚集在一起，在有的非枝晶初生晶粒中还存在残留的液相痕迹。

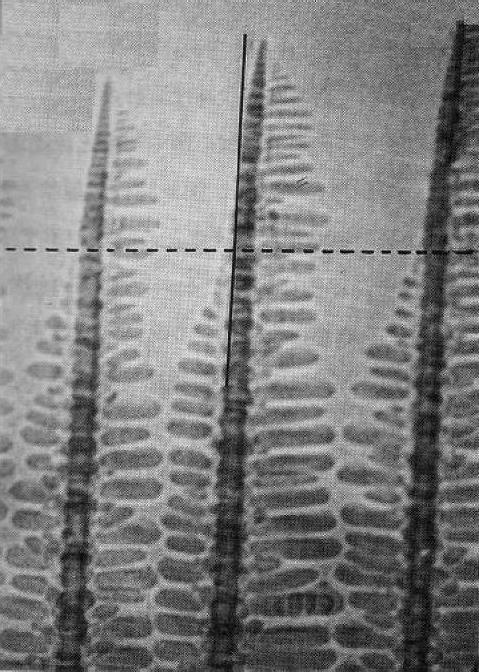
图5-7 向上成长的环己醇（Cyclohexanol）柱状树枝晶的先端到了虚线的位置时，液体从右向左以0.3mm/s速度流动（×25）

图5-8 Al-7%Si半固态无搅拌 浆料的淬火组织

图5-9 Al-7%Si半固态搅拌浆料的淬火组织 （剪切速率：500s^-1）

合金在凝固过程中，如果对其施加强烈搅拌，传统的枝晶状初生晶粒最终会转变为球状、椭球状或花瓣状。这种初生晶粒在搅拌过程中的转变机制是一个十分重要的基础理论问题，对这个问题的解决，将会加深对半固态组织形成的理解，且更有效地指导半固态金属或合金浆料、坯料的制备。由于对半固态金属或合金组织形成过程的研究难度较大，目前尚未形成统一和确定的理论，但也有人提出了几种半固态初生晶粒转变机制的假说，试图说明或解释初生晶粒在搅拌过程中的转变机制。

图5-10 搅拌条件下的球状初生 晶粒演化机制示意图

a）原始枝晶碎块 b）进一步长大后的枝晶碎块 c）玫瑰花状枝晶碎块 d）熟化后的玫瑰花状晶粒

e）球状晶粒

1.正常熟化引起的枝晶根部熔断论

Flemings等^[1]认为，在搅拌条件下，由于正常的熟化作用，枝晶臂会从其根部熔断，而搅拌引起的流动改变或促进了晶粒熟化时溶质的扩散，并将枝晶臂带往其他地方。这些熔断的初生枝晶臂（见图5-10a）在早期生长时会进一步枝晶化，如图5-10b所示。随着持续地搅拌剪切、初生枝晶之间的摩擦以及与液体之间摩擦和冲刷作用，也由于初生枝晶臂碎块的熟化作用，初生枝晶臂碎块逐渐转变为玫瑰花状，如图5-10c所示。随着初生枝晶臂碎块熟化的进行，初生枝晶臂碎块逐渐转变为更加密实的玫瑰花状，如图5-10d所示。在较高的剪切搅拌速率和较低的冷却速率下，初生枝晶臂碎块最后会转变为球状、椭球状或玫瑰花状，如图5-10e所示。当增加剪切速率和固相分数及降低冷却速率时，就能够加速从图5-10a到图5-10e的进程。初生固相晶粒的大小主要与凝固时的冷却速率有关，冷却速率越高，初生固相晶粒就越小，但当剪切速率大于某一数值时，初生固相晶粒也随剪切速率的增加而减小。

2.枝晶臂塑性弯曲和晶界浸润熔断论

Vogel等人^[6]在Al-20%Cu合金机械搅拌实验的基础上提出：α-Al枝晶在接近熔点温度附近虽然脆弱，但剪切不会使初生α-Al枝晶二次枝晶臂立即折断，剪切会使二次枝晶臂发生塑性弯曲，弯曲使枝晶臂根部产生附加位错群。这些位错将会因为该枝晶臂弯曲部位的回复和再结晶的发生而转变成晶界，那么该晶界就具有θ角大小的取向错误。若枝晶根部的晶界取向错误大于20°，该晶界所具有的晶界能σ_gb比固液界面能σ_sl大两倍以上，如Al的σ_gb大小为0.6J/m²，而Al的σ_sl为0.09J/m²，那么弯曲枝晶臂中的这种大角度晶界最终会被液体薄膜所完全浸润，最后该枝晶臂就会由于晶界引发的熔化而从枝晶主干上脱落下来，如图5-11所示。

3.冷却速度与对流速度耦合作用模型

随着对非枝晶组织形成机理认识的深入，人们也提出了一些新的理论，如电磁搅拌作用下的晶粒漂移和混合—抑制机制，认为在固液两相区，枝晶是难以机械断裂的，枝晶碎断并不是非枝晶组织形成的主要原因。由于电磁搅拌在熔体中产生的强烈混合和对流改变了传热和传质过程，使得晶粒在各个方向上的生长条件都相同，于是晶粒的生长类似于等轴晶生长的过程，搅拌冲刷作用使晶粒呈球状。但金属的不透明性，限制了人们对半固态组织形成过程中微观组织的动态演化过程进行直接的研究。李涛等人采用丁二腈—5%水透明模型合金，通过实时观察技术对半固态处理过程中的组织形成及演化机理进行了研究。结果表明，球晶是由液相形核长大产生的，而非传统的枝晶断裂所造成。因此，作者等人^[7]通过分析搅拌状态下晶粒生长的温度场和浓度场条件，将凝固速度（受冷却条件影响）与液体的流动速度（受搅拌的剪切速率影响）作为晶粒生长形态方程的函数，建立了搅拌状态下的冷却速度与对流速度耦合作用数学模型，并且模拟了晶粒在不同的凝固速度与剪切速率下的晶粒形态。

(www.xing528.com)

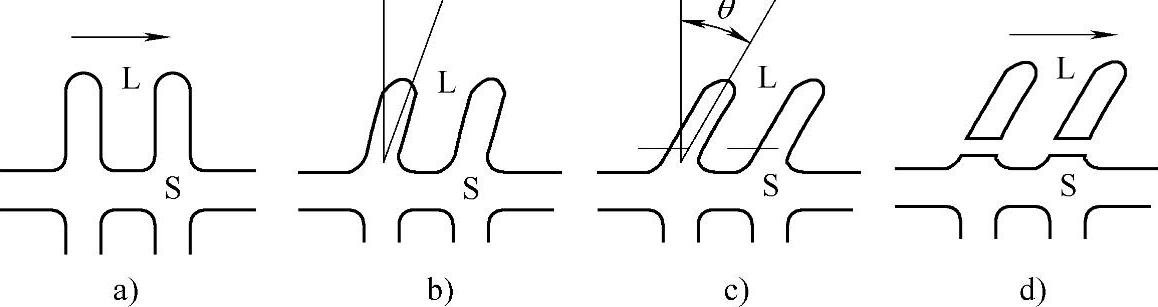
图5-11 枝晶断裂过程示意图

a）未变形的枝晶 b）枝晶臂弯曲 c）枝晶臂弯曲产生晶界 d）晶界被浸润，枝晶脱落

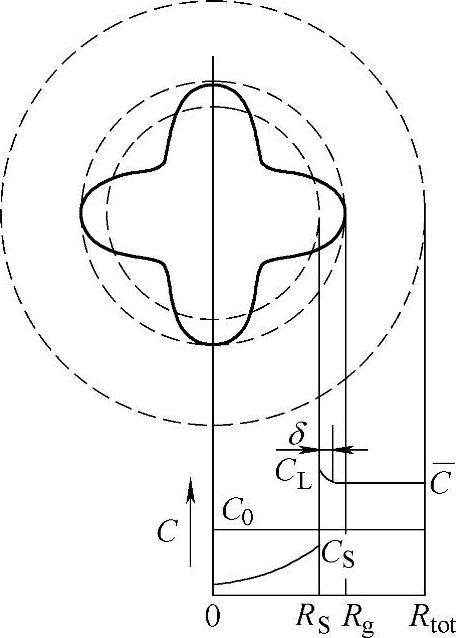
图5-12 晶粒形状及 溶质分布示意图

考虑搅拌不充分时，晶粒外观形状介于球状与树枝状之间，单个晶粒生长的固液界面的溶质分布如图5-12所示。图中C表示溶质质量分数，C₀为初始溶液的溶质质量分数，C_S和C_L分别为固液界面固相、液相的溶质质量分数，R_S为与晶粒截面积相等的圆的半径，R_g为晶粒尖端包围圆的半径，R_tot为凝固后晶粒平均半径。晶粒形状分数f_i定义为：与晶粒实际体积相等的球体的体积和晶粒尖端包围圆所形成的球体的体积之比，即

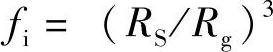
。f_i的值越大，晶粒越圆整，当f_i=1时，晶粒呈球状。

在半固态组织生成过程中，往往伴随着激烈的搅拌，因此液相中溶质分布比较均匀。但是在固液界面处依然存在一薄层液体，其流速为零，溶质只能借助扩散才能通过。由于扩散层的厚度δ远远小于晶粒尺寸，因此可以将固液界面的溶质扩散作为平界面的溶质扩散处理，当晶粒生长达到稳定状态后，固液界面的推进速度（即凝固速度）R可视为常数。

溶质分配特征微分方程式可用式（5-3）^[8]表示：

式中D_L——溶质在液相中的扩散系数（m²/s）；

R——生长速度（m/s）。

根据图5-12所示的模型，利用固相无扩散、液相有对流等边界条件，最后推导得到晶粒形状系数f_i与凝固速度R和液体对流速度v之间的关系为^[7]

由式（5-4）可知，半固态非枝晶晶粒的形态及圆整度由凝固速度R和液体对流速度v耦合作用控制。表5-1显示了根据上述数学模型的模拟结果。从模拟结果可知，在凝固速度保持一定的条件下，随着液体相对运动速度的增大，晶粒形状系数也增大，晶粒由枝晶状向球状转变。而在液体运动速度一定的条件下，凝固速度越大，晶粒形状系数越小，晶粒越倾向于成为枝晶状。

表5-1 晶粒形状模拟结果

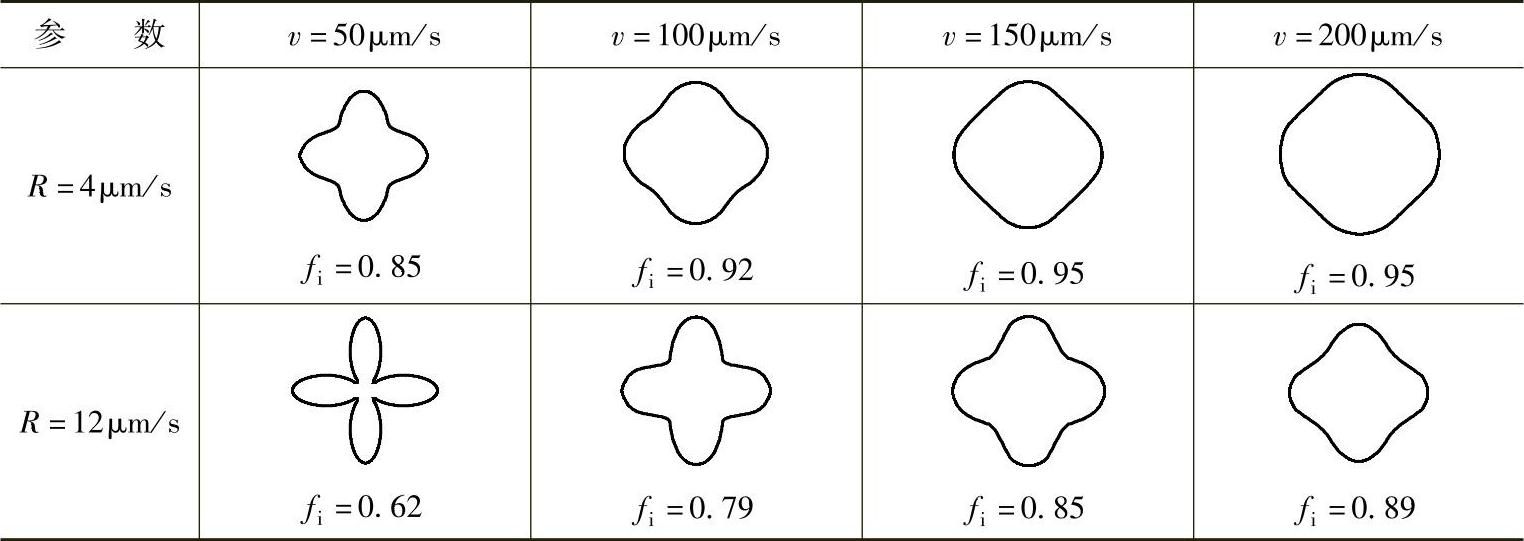
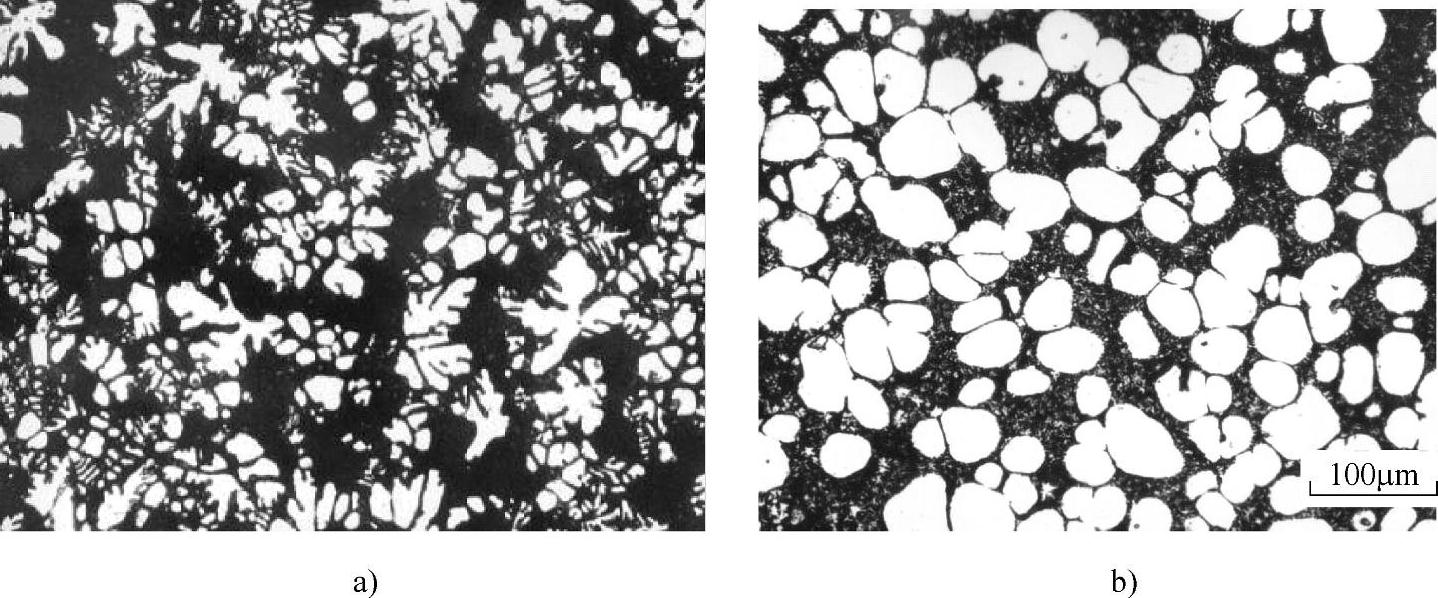
图5-13 AZ91D镁合金的半固态组织（R=10μm/s）^[7]

a）v_a=55μm/s b）v_b=220μm/s

对机械搅拌方法制备的AZ91D镁合金的半固态组织进行的研究表明，在不同的搅拌速度和冷却速度下，得到的是形态各异的半固态组织。图5-13所示为两图的冷却条件相同，即有相同的浇注温度和容器筒体温度，根据实际组织大小及凝固时间得出凝固速度R=10μm/s。与图5-13a、b所示对应搅拌下的液体对流速度v分别为55_μm/s、220μm/s，图5-13a所示虽然是半固态组织，但看得出初晶α相仍有较明显的枝晶形态，而图5-13b所示的初晶α相却是明显的非枝晶组织，且较圆整。根据式（5-4）计算得出f_i的值分别为0.69和0.91，参照表5-1中生长速度一定对流速度变化的结果可知，模拟计算结果与图5-13所示的实际结果比较接近。