ADAMS方程求解方案

运动学、静力学分析需求解一系列的非线性代数方程，ADAMS采用修正Newton-Raphson迭代算法迅速准确地求解。对动力学微分方程，根据机械系统的特性，可选择不同的积分算法。对刚性系统，采用变系数BDF（Backwards Differentiation Formula）刚性积分程序，它是自动变阶、变步长的预估矫正法，在积分的每一步采用了修正的Newton- Raphson迭代算法；对高频系统，采用坐标分配法和ABAM（Adams-Bashforth-Adams-Moulton）方法。与之相应，ADAMS/Solver中包含了3个功能强大的求解器：

ODE求解器（求解微分方程），采用刚性或非刚性积分算法；非线性求解器（求解代数方程），采用Newton-Raphson迭代算法；线性求解器（求解线性方程组），采用高斯消元法，并引入稀疏矩阵技术。其求解过程如图1-3所示。

ADAMS/Solver有5个强大的数值积分程序，其中4个为变阶、变步长的刚性积分程序（GSTIFF，SI2_GSTIFF，DSTIFF，WSTIFF）,使用最多的是变系数的BDF（Backwards Differentiation Formula）方法，它是自动变阶、变步长的预估矫正法。第五个为非刚性积分程序，采用了Adams-Bashforth-Adams-Moulton算法，对于常用的4个BDF积分程序，其预估矫正求解过程分3个阶段实现：

（1）预估阶段。

①根据泰勒展开式预估在t_n+1时刻y及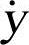的值：

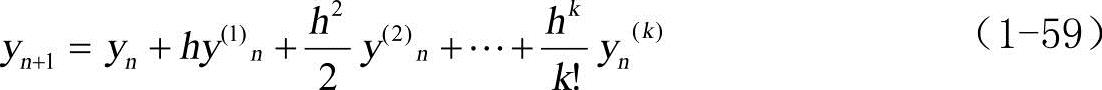
式中，h=t_n+1−t_n为步长。

对于GearStiff积分程序的格式为：

式中，β₀,α_i为Gear积分系数。

图1-3 ADAMS求解过程

（2）校正阶段。

②求解系统方程G，如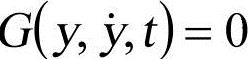，则方程成立，此时y为方程解，否则继续。(www.xing528.com)

③求解Newton-Raphson线性方程得到∆y，以更新y，使系统方程G更近于成立。

式中，J为系统雅可比矩阵。

④利用Newton-Raphson迭代，更新y

y_k+1=yk+∆y_k （1-63）

⑤重复步骤②～④直到∆y足够小。

（3）误差控制阶段。

⑥预估积分误差并与误差精度比较，如误差过大则摒弃此步。

⑦计算优化的步长h和阶数k。

⑧如时间已到结束时间，则停止仿真，否则t=t+∆t进入步骤1。其积分程序的程序逻辑如图1-4所示。

图1-4 积分程序逻辑

3种STIFF刚性积分程序中WSTIFF稳定性最好，但计算效率不高；GSTIFF计算效率最高，但稳定性最差；DSTIFF的计算效率和稳定性则介于两者之间，这3种积分程序适用于模拟刚性机械系统，而ABAM积分程序适用于模拟经历突变的系统或高频系统。ADAMS缺省的积分程序为GSTIFF，以提高计算效率，但较容易出现数值发散现象。