ADAMS建模方法详解

ADAMS采用的是欧拉—拉格朗日方法。其结构形式属于第二类模型。拉格朗日方法广泛应用于多刚体力学，Chace选取系统内每个刚体的质心在惯性参考系中的3个直角坐标和欧拉角为笛卡尔广义坐标，编制了ADAMS程序。Haug选取系统内每个刚体的质心在惯性参考系中的3个直角坐标和欧拉参数为笛卡尔广义坐标，编制了DADS程序。由于在选定坐标后，利用带乘子的拉格朗日方程处理后导出的以笛卡尔广义坐标为变量的动力学方程是与广义坐标数目相同的带乘子的微分方程，所以所得的多刚体动力学模型是混合的微分-代数方程组，特点是方程数目相当大，且常为刚性的。萘斯在ADAMS中用了吉尔（Gear）等的刚性积分算法，并采用了稀疏矩阵技术提高了计算效率。

1.ADAMS多刚体方程基础

（1）动能。

平动动能为：

式中，M为刚体质量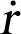；为刚体质心速度矢量。转动动能为：

式中，ω为刚体角速度；I为刚体转动惯量。

总动能为：

K=K_t+K_r （1-52）

（2）动量。

与广义坐标q_j相关联的广义动量为：

平动动量P_x，P_y，P_z：

转动动量P_ψ，P_φ，P_θ：

式中，S、C分别代表正、余弦函数；ψ、φ、θ为欧拉角。

（3）笛卡儿广义坐标。ADAMS采用6个笛卡儿广义坐标描述一个刚体的位形，利用其质心的3个直角坐标x、y、z确定位置，连体基的3个欧拉角ψ、φ、θ确定方位，这6个量称为笛卡儿广义坐标，可以完全描述系统内各个刚体的位形。

2.ADAMS软件的多刚体方程

ADAMS根据机械系统的模型，自动建立系统的拉格朗日运动方程，对于每个刚体，列出对应于6个广义坐标带乘子的拉格朗日方程及相应的约束方程：

式中，i=1,…,n，j=1,…,m；q_j为描述系统的广义坐标；Φ_i为系统的约束方程；F_j为广义坐标方向上的广义力；λ_i为拉氏乘子。

上式可写作如下形式：

式中，；。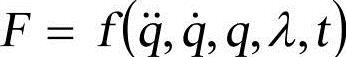

动能的定义为：(www.xing528.com)

代入式（1-55），合并成简洁的矩阵形式为：

式中，；；M=diag[M₁M₂…M_n]；。

对上述代数—微分方程，ADAMS将二阶微分方程降阶为一阶微分方程来求解。即ADAMS将所有拉格朗日方程均写成一阶微分方程形式，并引入，得到

式中，。

综上所述，对多刚体系统ADAMS将列出以下方程：

（1）刚体运动方程。

6个一阶动力学方程（力和加速度关系）：

6个一阶运动学方程（位置和速度关系）：

3个转动动量的定义方程：

（2）约束代数方程。

（3）外力的定义方程（重力除外）。

（4）自定义的代数—微分方程。

写成矩阵形式如下：

刚体运动方程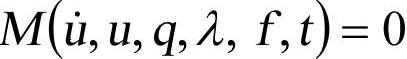

系统约束方程

系统外力方程

自定义代数—微分方程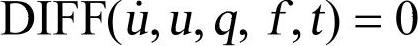

式中，q为笛卡儿广义坐标；u为广义坐标的微分；f由外力和约束力组成；t为时间。

令为状态向量，系统方程可写为：