1.外加载荷
在ADAMS软件中,外加载荷包括单点力与扭矩、分布式载荷以及残余载荷3部分。
(1)单点力与扭矩。施加于柔性体上某一标记点的单点力和扭矩必须投影到系统的广义坐标上才能起作用,力和扭矩以矩阵形式写出,在标记点K的局部坐标系下表示为:
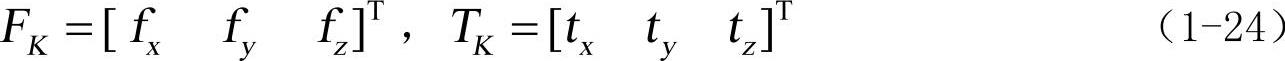
广义力Q由广义平动力、广义扭矩(以欧拉角表示的广义力)和广义模态力组成,可表示为:

平动坐标下的广义力可以通过转换单点力FK到全局坐标基er下来获得,即:
QT=AFK (1-26)
式(1-26)中,A为标记点K上的坐标系相对于全局坐标的欧拉角变换矩阵,可以表示为:Agk=AgbAbpApk,如图1-2所示,Agb为局部坐标系B点相对于全局坐标系的转换矩阵,即方向余弦阵;Abp为因节点P的小变形引起的标记坐标的方位变化而引入的转换矩阵;Apk为定义在柔性体上标记点处的坐标系相对于P点坐标系的常值变换矩阵。
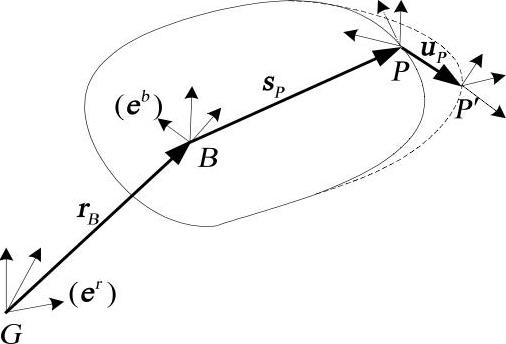
图1-2 柔性体变形模型
作用在柔性体标记点处的合力矩,可用相对于全局坐标的矢量矩阵表达为:

式中,p为从局部坐标基eb到受力点处的位移矢量,用斜方阵表示,上式可改写为:

将物理坐标系下的力矩向基于欧拉角的坐标系转换,并利用式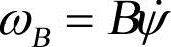 ,可得广义合力矩为:
,可得广义合力矩为:
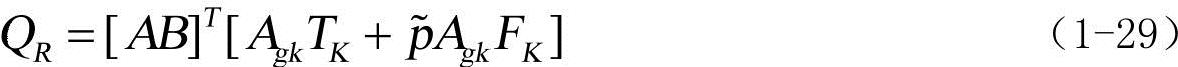
通过投影单点力和单点力矩到模态坐标上,可得到P点处的广义模态力。
如在标记点K处施加力FK和力矩TK,通过转换到全局坐标上,即有:FI=AgkFK,TI=AgkTk,并将FI投影到平动模态坐标、将TI投影到角模态坐标上,可得广义模态力:

式中,ΦP和ΦP*对应于节点P处的平动和转动自由度的模态斜方阵。由于模态矩阵Φ只定义在节点,故单点力和单点力矩只能施加于节点处。
(2)分布式载荷。在ADAMS软件上,分布式载荷可以通过MFORCE的方式来创建。通常在FEM软件中有运动方程:

式中,M和K为柔性体上有限单元的质量和刚度矩阵;x和F为物理节点的自由度矢量和载荷矢量。
利用模态矩阵Φ将式(1-31)转换到模态坐标q下,有:

上式可简化为:

式中,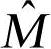 和
和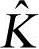 分别为广义质量和刚度矩阵;f为模态载荷矢量。
分别为广义质量和刚度矩阵;f为模态载荷矢量。
节点力矢量在模态坐标上的投影为:

式中如果F是时间的函数则求解时计算开销太大,一种替代的方法是假设空间依赖性和时间依赖性可以分开,把载荷F看成一系列依赖于时间的静态载荷的线性组合,即:

载荷在模态坐标上的投影计算可在有限元文件MNF过程中完成,而不必在ADAMS仿真中重复进行。如果定义一系列静载荷为载荷矢量,并使其与系统响应显性相关,即表示成f(q,t)的形式,则模态力又可表示为:
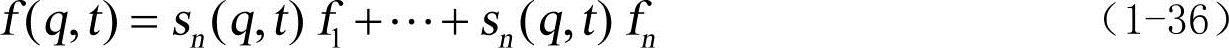
(3)残余载荷。先前的假设是施加的载荷向模态坐标的投影已实现,即式(1-34)成立。然而由于模态截断,很多情况下施加的力并不能进行投影,这些力被称为残余载荷,可以将其看为已投影到了被截断的高阶模态坐标上。残余载荷可表示为:(https://www.xing528.com)

与残余载荷相关的是残余矢量,可看成是把残余载荷施加于柔性体时产生的变形。残余矢量可被当作模态振型加入到Craig-Bampton模态基中,增强的模态基完全能够捕捉残余载荷,否则,残余力的丢失不可避免。
2.多柔体系统的能量
(1)动能和质量矩阵。考虑节点P变形前后的位置、方向和模态,柔性体的广义坐标可以表示为:

速度表达式(2-19)在系统广义坐标式(1-38)的时间导数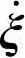 中表示为:
中表示为:

柔性体的动能为:
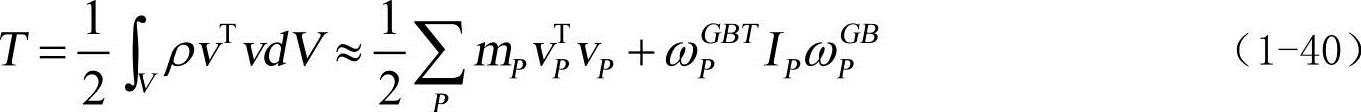
式中,mP和IP分别为节点P的节点质量和节点惯性张量;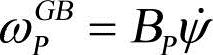 ,为点B相对于全局坐标基的角速度在局部坐标基中的斜方阵表示。将式(1-39)和关系式
,为点B相对于全局坐标基的角速度在局部坐标基中的斜方阵表示。将式(1-39)和关系式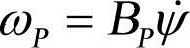 代入式(1-40),得到动能的广义表达式:
代入式(1-40),得到动能的广义表达式:

上式中的质量矩阵M(ξ)为3×3维的方阵,表示为:
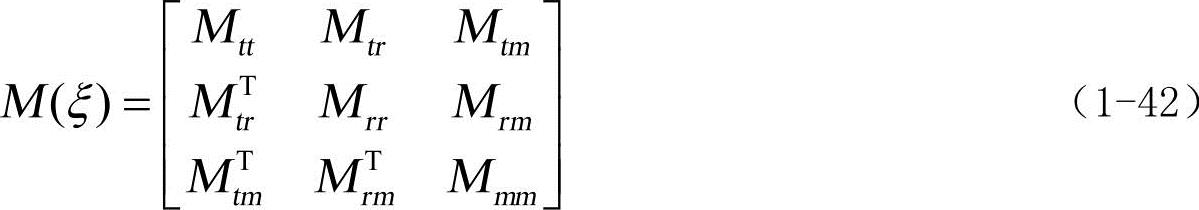
其中下标t,r,m分别表示平动、旋转和模态自由度。质量矩阵的6个独立分量分别表示为:
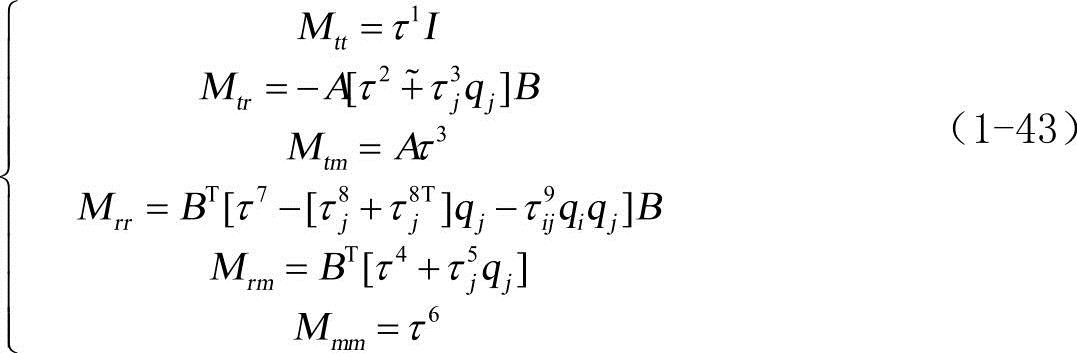
式(1-43)中可以明显看出质量矩阵与模态坐标显性相关,而且由于引入转换矩阵A和B,质量矩阵也与系统的方向坐标显性相关。质量矩阵中的9个惯性时不变矩阵τ1~τ9可通过计算有限元模型的N个节点信息在预处理过程中一次性得到,从而简化运动微分方程的求解。节点信息包括:每个节点的质量mP,未变形时的位置矢量sP以及模态矩阵ΦP。
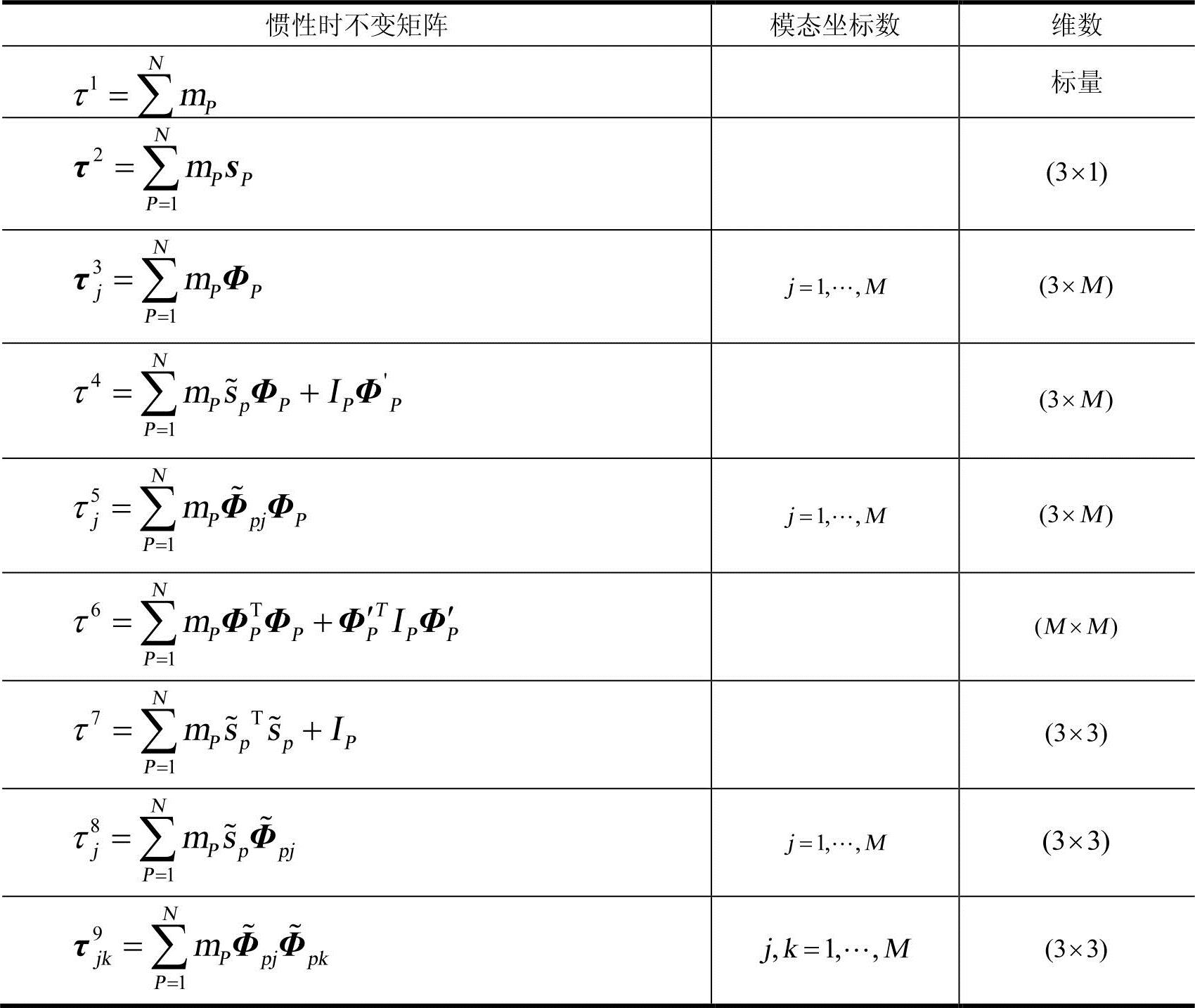
其中9个惯性时不变矩阵见表1-1。
(2)势能和刚度矩阵。势能一般分为重力势能和弹性势能两部分,可用下列二次项表示:

在弹性势能中,K是对应于模态坐标q的结构部件的广义刚度矩阵,通常为常量。重力势能Wg表示为:
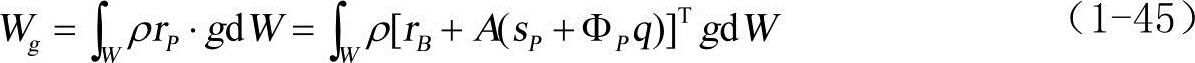
式中,g表示重力加速度矢量,重力fg可对Wg求导得:
表1-1 惯性时不变矩阵列表
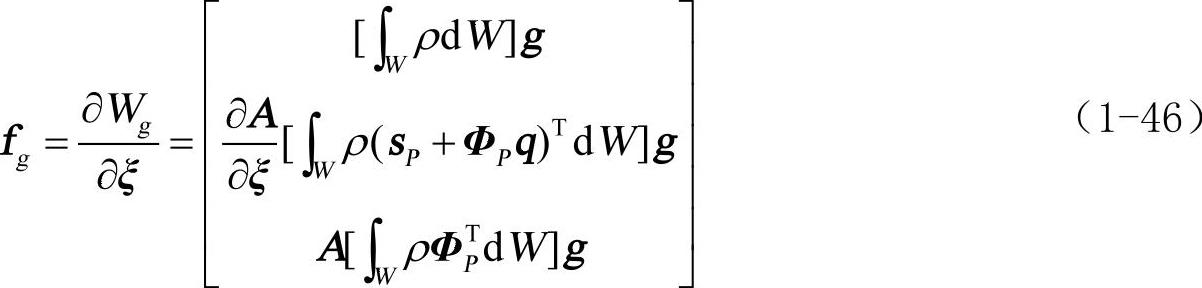
(3)能量损失和阻尼矩阵。阻尼力依赖于广义模态速度并可以从下列二次项中推导得出:

上式称为Rayleigh能量损耗函数。矩阵D包含阻尼系数dij,它是常值对称阵。当引入正交模态振型时,阻尼矩阵可用对角线为模态阻尼率ci的对角阵来表示。对于每一个正交模态的阻尼率都可以取不同值,而且还能以该模态的临界阻尼cicr比值形式给出。
3.多柔体动力学方程
柔性体的运动方程从下列拉格朗日方程导出:

式中,Ψ为约束方程;λ为对应于约束方程的拉氏乘子;ξ为如式(1-38)定义的广义坐标;Q为投影到ξ上的广义力;L为拉格朗日项,定义为L=T−W,T和W分别表示动能和势能;Γ为能量损耗函数。
将求得的T,W,Γ代入式(1-48),得到最终的运动微分方程为:
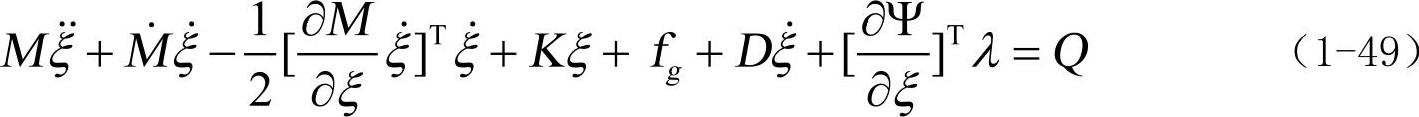
式中,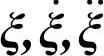 为柔性体的广义坐标及其时间导数;M,
为柔性体的广义坐标及其时间导数;M, 为柔性体的质量矩阵及其对时间的导数;
为柔性体的质量矩阵及其对时间的导数;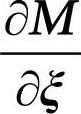 为质量矩阵对柔性体广义坐标的偏导数,是(M+6)×(M+6)×(M+6)维张量;M为模态数。
为质量矩阵对柔性体广义坐标的偏导数,是(M+6)×(M+6)×(M+6)维张量;M为模态数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




