柔性体系统中的坐标系如图1-1所示,包括惯性坐标系(er)和动坐标系(eb)。前者不随时间变化,后者是建立在柔性体上,用于描述柔性体的运动。动坐标系可以相对惯性坐标系进行有限的移动和转动。动坐标系在惯性坐标系中的坐标(移动、转动)称为参考坐标。
与刚体不同,柔性体是变形体,体内各点的相对位置时时刻刻都在变化,只靠动坐标系不能准确描述该柔性体在惯性坐标系中的位置,因此,引入弹性坐标来描述柔性体上各点相对动坐标系统的变形。这样柔性体上任一点的运动就是动坐标系的“刚性”运动与弹性变形的合成运动。由于柔体上各点之间有相对运动,所以动坐标系的选择不是采用连体坐标系,而需要采用随着柔性体形变而变化的坐标系,即“浮动坐标系”。

图1-1 柔性体上节点P的位置
在研究多柔体系统时,合适的坐标系是非常重要的。在确定浮动坐标系时有两点准则:便于方程建立求解;柔性体刚体运动与变形运动的耦合尽量小。目前常见的浮动坐标系大致有5种:局部附着框架、中心惯性主轴框架、蒂斯拉德框架、巴克凯恩斯框架以及刚体模态框架,采用哪一种视实际情况而定。
在分析刚体平面运动的时候,把复杂的刚体平面运动分解为几种简单的运动。在对柔性体的运动,尤其是在小变形的情况下,也可以采用类似的方法。如某柔性体从位置L1运动到位置L2,其间运动可以分解为:刚性移动→刚性转动→变形运动。对于柔性体上任意一点P,其位置向量为:
r=r0+A(sp+up) (1-20)
式中,r为P点在惯性坐标系中的向量,r0为浮动坐标系原点在惯性坐标系中的向量;A为方向余弦矩阵;sp为柔性体未变形时P点在浮动坐标系中的向量;up为相对变形向量,up可以用不同的方法离散化,与讨论平面问题相同,对于点P,该单元的变形采用模态坐标来描述,有:(https://www.xing528.com)

式中
Φp为点P满足里兹基向量要求的假设变形模态矩阵;q为变形的广义坐标。
柔性体上任一点的速度向量及加速度向量,可以对式(1-20)求对时间的一阶导数和二阶导数得到:
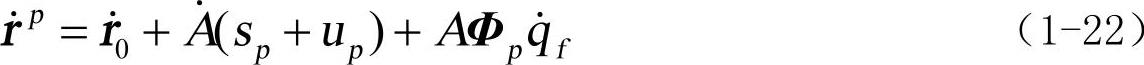
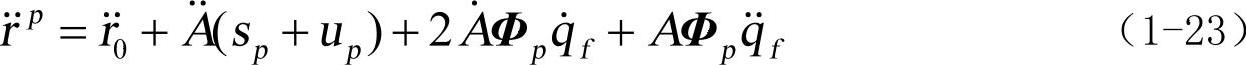
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




