多刚体系统的动力学模型分析

随着多体动力学的发展，目前应用于多刚体系统动力学的方法主要有以下几种：牛顿-欧拉法(Newton-Euler)、拉格朗日方程法、图论(R-W)法、凯恩法、变分法、旋量法等。在求解机械系统（多体系统）动力学控制方程时，常常（如ADAMS软件等）采用3种功能强大的变阶和变步长积分求解程序，即BDF、Gstiff和Dstiff来求解稀疏耦合的非线性微分—代数方程。ADAMS用刚体i的质心笛卡儿坐标和反映刚体方位的欧拉角（或广义欧拉角）作为广义坐标，即q_i=[x,y,z,ψ,θ,ϕ]_i^T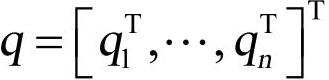，。采用拉格朗日乘子法建立系统运动方程：

完整约束方程时：f(q,t)=0

非完整约束方程时：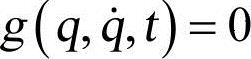

式中，T为系统动能；Q为系统广义坐标列阵；ρ为对应于完整约束的拉氏乘子列阵；Μ为对应于非完整约束的拉氏乘子列阵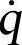；为系统广义速度列阵。

定义1 系统动力学方程：对于有N个自由度的力学系统，确定N个广义速率以后，即可计算出系统内各质点及各刚体相应的偏速度及偏角速度，以及相应的N个广义主动力及广义惯性力。令每个广义速率所对应的广义主动力与广义惯性力之和为零，所得到的N个标量方程即称为系统的动力学方程，也称为凯恩方程：

F^(r)+F^∗(r)=0（r=1，2，…，N） （1-5）

写成矩阵形式为：

F+F^*=0 （1-6）

式中F、F^∗为N阶列阵。

定义为：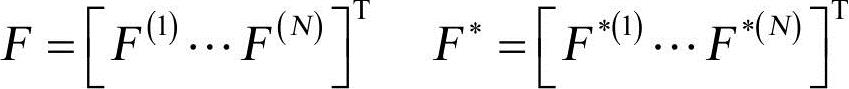

在系统运动方程（1-4）中令：。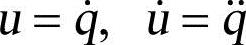

则系统运动方程可化成动力学方程为：

式中，u为广义速度列阵；λ为约束反力及作用力列阵；G为描述广义速度的代数方程列阵；Φ为描述约束的代数方程列阵。

定义2 Gear预估—校正多步算法：继承ADAMS四阶预估—校正变阶算法，采用变步长法，其步骤如下：(www.xing528.com)

（1）f(x，t)的Jacobi矩阵的计算。

（2）校正的迭代运算，第二步运行时要适当给出迭代精度与单步积分精度，否则会出现迭代收敛所要求的步长小于单步积分精度要求的步长，造成计算步长反复放大缩小。

定义系统的状态矢量y=[q^T,u^T,λ^T]，用Gear算法求解系统运动方程，根据当前时刻的系统状态矢量值，用Taylor级数预估下一个时刻系统的状态矢量值：

其中时间步长h=t_n+1−t_n，这种预估算法得到新的时刻的系统状态矢量值通常不准确，可由Gear法K+1阶积分进行校正：

式中y_n+1是y(t)在t=t_n+1时的近似值，β₀,α_i为Gear积分系数值，也可写成：

则系统动力学方程在t=t_n+1时刻展开，得：

定义3 Newton—Raphson算法：求解非线性方程组Φ（x）=0，其中共有n个方程，即：Φ=（Φ₁…Φ_n）T，变量x阵为n阶列阵。N-R算法的关键是如何选取适当的初值，如果矩阵为非奇异，则解是唯一的。使用修正的N-R算法求解上述非线性方程，其迭代校正公式为：

式中j表示第j次迭代，∆q_j=q_j+1−q_j,∆u_j=u_j+1−u_j,∆λ_j=λ_j+1−λj

由式（1-12）知：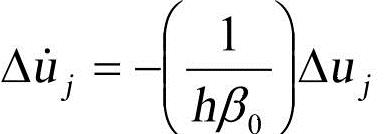

由式（1-14）知：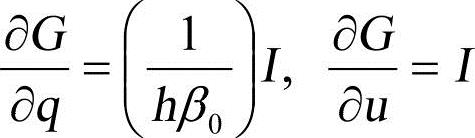

则写成矩阵形式为：

式中，左边的系数矩阵称为系统的Jacobi矩阵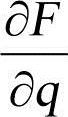；是系统的刚度矩阵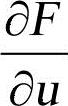；是系统阻尼矩阵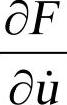；是系统质量矩阵。通过分解系统Jacobi矩阵求解∆q_j,∆u_j,∆λ_j，计算出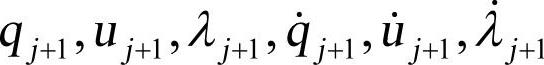，重复上述步骤，直到满足收敛条件，判定积分误差限，确定是否接受该解。