计算任意位置的各序电流和电压在序网中的应用

要计算网络中任意处的电流和电压，必须首先求得各序网络中该处电流和电压的序分量，然后再将该处电流和电压的序分量合成，即可得该处的三相电流和电压。

1.各序电流分布计算

由于各序网络是对称网络，因此三相对称短路时有关电流分布的基本计算方法，例如，并联支路电流可按阻抗反比分配法、基尔霍夫电流定律（∑＝0）法及电流分布系数法等计算方法，在求不对称故障的各序电流分布时同样适用。

负序网络和零序网络是无源网络，当通过复合序网求得故障点处的序电流后，利用电流分布系数计算电流分布较为简便。对于给定的短路点，负序和零序网络中各支路点电流分布系数都是确定的。在该点发生各种不对称短路时，在短路过程的任一时间，都可应用这些分布系数计算网络中的电流分布。

根据图9-21所示系统接线作出其负序网络，如图9-22所示。

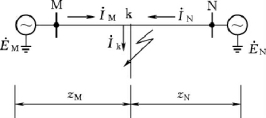
图9-21　电流分布计算系统接线图

图9-22　负序电流的分布计算网络图

由图9-22可求出各支路的负序电流，即

式中 Z∑2——M、N支路的组合等值负序阻抗；

CM2、CN2——M及N支路中的负序电流分布系数。

其中

且满足

可见，当故障点总的负序电流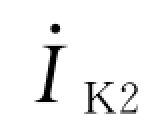及网络参数均已知时，即可求出M、N支路的负序电流。

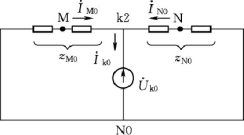
系统的零序网络图如图9-23所示。零序电流的分布计算与负序电流方法相同，各参数之间的关联也相同。

(www.xing528.com)

图9-23　零序电流的分布计算网络图

正序网络是有源网络，求得故障处的I后，可以利用叠加原理把正序网络分解成正常情况和故障情况两部分，如图9-24所示。

正常情况下各支路电流可由潮流计算得到。在实用计算中，假定正常运行时系统为空载，故障情况时故障点只有正序分量电流，网络中无电源，故仿照负序或零序网络的方法也很容易求出任意处的支路电流。对于任意处节点电压的求解方法类似求支路电流。

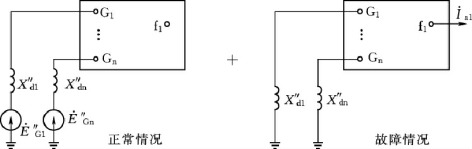
图9-24　正序网分解图

利用电流分布系数法求各支路电流，好处是在同一种运行方式下，网络中同一点发生不同类型的故障时，每序网络的电流分布系数是相同的。因此，只要第一次计算时求出某支路的各序电流分布系数，用其乘上不同类型短路时短路点相应的总电流，即可得到这时该支路的相应序的分支电流。

2.各序电压分布计算

在图9-25所示的简单系统中，当k点发生了三相短路时，M母线上的基准相（a相）电压，可以表示为

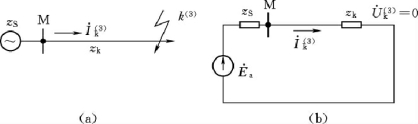
图9-25　计算三相短路电压分布的系统接线图

（a）系统接线图；（b）电流流通图

上式表明，线路上某点的电压等于故障点的电压加上从故障点到所求点阻抗上的压降。这一关系式用在计算不对称短路时，要按每一序网络分别进行计算。例如，在图9-26中k点发生不对称短路时，求M点电压的计算步骤大致如下：

图9-26　不对称故障时电压分布计算图

（a）系统接线图；（b）各序网络图

图9-27示出简单系统在各种不同类型短路时，各序电压有效值的分布情况。正序网中，电源正序电压最高，越靠近短路点正序电压越低，三相短路时短路点电压为零。负序和零序网中，短路点的负序和零序电压最高，节点距故障点越远，即越靠近电源点，负序和零序电压越低，在电源点，负序电压等于零，由于变压器是Y0／Δ接法，所以零序电压在变压器三角形一侧的出线端就已经降为零了。上述结论可推广到一般系统。

网络中各点电压的不对称程度主要由负序分量决定。负序分量越大，电压越不对称。比较图9-27中各个图形可以看出，单相短路时电压的不对称程度要比其他类型的不对称短路时小些。不管发生何种不对称短路，短路点的电压最不对称，电压不对称程度将随着和短路点距离的增大而逐渐减弱。

上述求网络中各序电流和电压分布的方法，只对与短路点有直接电气联系的部分网络，才可获得各序量间的相位关系。在由变压器联系的两段电路中，由于变压器绕组的连接方式，变压器一侧各序电压对另一侧可能有相位移动，并且正序分量与负序分量的相位移动也可能不同。下面我们将讨论这一情况。