无限大容量电源供电系统的三相短路电流分析

图7-8所示为无限大容量系统供电的三相对称短路。

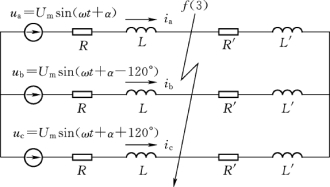
图7-8　无限大容量电源供电系统的三相对称短路

短路发生以前电路处于稳定状态，由于三相电路对称，可以写出a相的电压和电流的表达式分别为

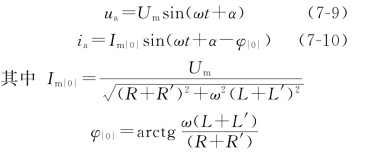
式中 R+R'和L+L'——分别为短路前每相电路的电阻和电感；

|0|——φ的下标，表示短路前的状态；

α——电源电势初始相角，即t＝0时的相位角。

当电路在f点突然发生三相短路后，这个电路即被分成两个独立的回路，左侧的回路仍与电源连接，但每相阻抗由原来的（R+R′）+jω（L+L′）减小为R+jωL。短路后电源供给的电流从原来的稳态值逐渐过渡到由电源和新阻抗R+jωL所决定的短路稳态值。而右侧的回路则由于没有电源，该回路电流逐渐衰减为零。

假定短路在t＝0时刻发生，由于左侧电路仍为三相对称电路，可以只研究其中的一相，其他两相由对称关系可以得出。

对于a相，其电流的瞬时值应满足如下微分方程：

式（7-11）是一个一阶常系数线性非齐次微分方程，它的解即为短路时的全电流。

求解式（7-11），得到a相短路电流瞬时值的表达式为(www.xing528.com)

式（7-12）即为a相短路电流的表达式。由于三相电路对称，只要用α-120°和α+120°代替式（7-12）中的α就可分别得到b相和c相短路电流表达式。现将三相短路电流表达式综合如下：

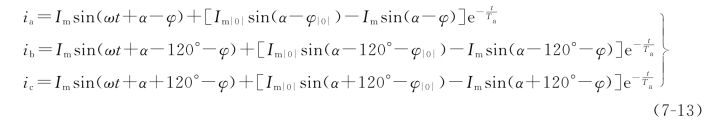
由式（7-12）可知，短路电流中包含有两个分量，其一是随时间作周期性变化的分量，称为交流分量或称为周期分量，其幅值大小取决于电源电压幅值和短路回路的总阻抗；其二是幅值随时间而衰减的分量，称为直流分量或称非周期分量，产生直流分量的原因是，电感中的电流在突然短路瞬时的前后不能突变。

根据式（7-12）所作的短路电流变化曲线如图7-9所示。

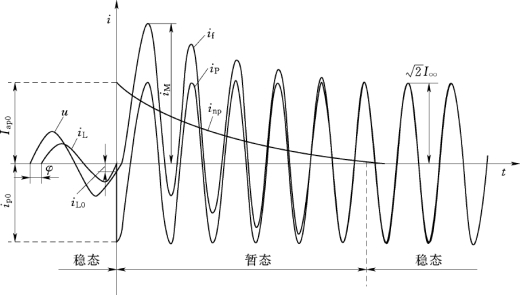
图7-9　无限大容量电源供电系统短路电流变化曲线

由图7-9可知，由于存在直流分量，短路电流曲线的对称轴不再与时间轴对称，而直流分量本身就是短路电流曲线的对称轴。因此，当已知一短路电流曲线时，可以应用这个性质把直流分量从短路电流曲线中分离出来，即将短路电流曲线的两根包络线间的垂直线等分。

在电源电压幅值和短路回路阻抗恒定的情况下，短路电流交流分量的幅值是一定的，因而短路电流的非周期分量起始值的大小决定了短路电流瞬时值的大小。直流分量起始值越大，短路电流的最大瞬时值越大。短路电流起始值的大小与电源电压的初始相角α及短路前回路中的电流值Im|0|有关。

若不考虑负荷电流对短路电流的影响，即认为短路前为空载（Im|0|＝0），则式（7-12）可进一步简化为

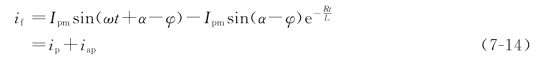
式中 ip——短路电流周期分量；

iap——短路电流非周期分量。