电力系统有功功率-频率的静态特性

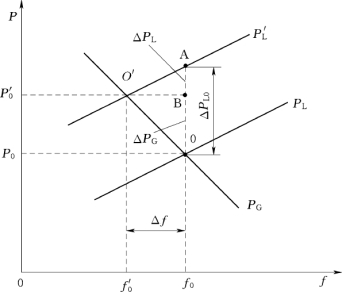
图4-6　电力系统功率—频率静态特性

要确定电力系统的负荷变化引起的频率波动，需要同时考虑负荷与发电机组两者的调节效应。为了方便起见，先只考虑一台机组和一个负荷的情况。我们把负荷及发电机组两者的静态特性画在同一张图上，如图4-6所示。在原始运行状态下，系统负荷的功频静特性为PL，它同发电机组的功频静特性PG的交点O是系统的原始运行点，这时系统的频率为f0（理想状态时为额定频率fn），发电机组的功率（也就是负荷的功率）为P0。这就是说在频率为f0时达到了发电机组有功输出与系统的有功需求之间的平衡。

现在假定系统的负荷增加了ΔPL0，其特性曲线变为P′L，发电机组仍是原来的特性。那么新的稳态运行点将由P′L和发电机组的静态特性的交点O′决定，与此相应的系统频率为f′0。由图可见，由于频率变化了Δf，且Δf＝f′0-f0＜0，发电机组的功率输出的增量为

由于负荷的频率调节效应所对应的负荷功率变化为

当频率下降时，ΔPL是负的。故负荷功率的实际增量为

或者(www.xing528.com)

上式说明，系统负荷增加时，在发电机组功频特性和负荷本身的调节效应共同作用下又达到了新的功率平衡。即是一方面负荷增加，频率下降，发电机按有差调节特性增加输出；另一方面负荷实际取用的功率也因频率的下降而有所减少。

在式（4-15）中

称为系统的功率—频率静特性系数，或系统的单位调节功率。它表示在计及发电机组和负荷的调节效应时，引起频率单位变化的负荷变化量。它取决于各发电机组的单位调节功率及负荷的单位调节功率。根据K值的大小，可以确定在允许的频率偏移范围内，系统所能承受的负荷变化量。显然，K的数值越大，负荷增减引起的频率变化就越小，频率也就越稳定。

将式（4-16）中的KG和KL分别用其标幺值表示时有

如果在初始状态下，发电机组已经满载运行，即是运行在图4-7中的A点，在A点以后，发电机组的静态特性将是一条与纵轴平行的直线，在这一段KG＝0。当系统的负荷再增加时，由于发电机已经没有可调节的容量，不能再增加输出了，只有靠频率的下降后负荷本身的调节效应的作用来取得新的平衡。这时K*＝KL*，由于KL*的数值很小，所以负荷增加所引起的频率下降就相当严重了。由此可见，系统中有功功率电源的出力不仅应满足在额定频率下系统对有功功率的需求，而且为了适应负荷的增长，还应该有一定的备用容量。

图4-7　发电机组满载时的功率—频率静态特性