电力系统负荷功率的频率静态特性分析

电力系统中的用电设备从系统中取用的有功功率的多少，与用户的生产状况有关，与接入点的系统电压有关，还与系统的频率有关。假定前两种因素不变，仅考虑有功功率负荷随频率变化的静态关系，称为负荷的功率—频率静态特性。

系统中根据所需的有功功率与频率的关系可将负荷分成以下几种：

（1）与频率变化无关的负荷，如电弧炉、电阻炉、照明和整流负荷等。

（2）与频率的一次方成正比的负荷，负荷的阻力矩等于常数的属于此类，如球磨机、金属切削机床、往复式水泵、压缩机和卷扬机等。

（3）与频率的二次方成正比的负荷，如变压器中的涡流损耗。

（4）与频率的三次方成正比的负荷，如通风机、静水头阻力不大的循环水泵等。

（5）与频率的高次方成正比的负荷，如静水头阻力很大的给水泵。

于是，整个系统的负荷功率与频率的关系可以写成

式中 PL——频率为f时系统的有功功率负荷；

PLN——频率为额定频率fN时系统的有功功率负荷；

a0、a1、…、an——与频率的0、1、…、n次方成正比的负荷占系统总负荷PL的百分数。

显然，当f＝fN时，PL＝PLN，此时a0+a1+a2+…+aN＝1，若以PLN为基准值，在式4-2两边除以PLN，则得到标幺值形式的功率—频率特性表达式：

显然，在额定频率下标幺值f*＝1及PL*＝1。在实际计算中，多项式4-3通常只需取到频率的3次方为止，因为与频率的更高方次成正比的负荷所占的比重很小，可以忽略。

在电力系统实际运行中，频率的容许变化范围很小，而且在负荷的组成中一次方关系的负荷比例较大，因此，系统综合负荷的频率静态特性曲线近似成线性关系，如图4-3所示。

图中直线的斜率为

图4-3　负荷的有功功率—频率静态特性曲线(www.xing528.com)

用标幺值表示为

有名值和标幺值的变换关系为

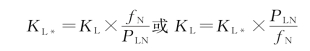
式中KL、KL*称为负荷的频率调节效应系数（也称为负荷的单位调节功率）。它反映了系统负荷对频率的自动调整作用：当频率下降时，系统有功负荷自动减少；当频率上升时，系统有功负荷自动增加。KL*的数值取决于全系统各类负荷的比重，不同系统或者同一系统不同时刻KL*值都可能不同，它是不能整定的。

在实际系统中，KL*可以通过试验或计算求得，一般取1～3。这表明频率变化1%，有功负荷相应地变化1%～3%。调度部门常以此数据作为考虑因系统频率降低需减少负荷或低频事故计算切除负荷的依据。

【例4-1】 某电力系统中，与频率无关的负荷占30%，与频率一次方成正比的负荷占40%，与频率二次方成正比的负荷占10%，与频率三次方成正比的负荷占20%。求系统频率由50Hz降到48Hz和45Hz时，相应负荷功率的变化百分值及其负荷的频率调节效应系数。

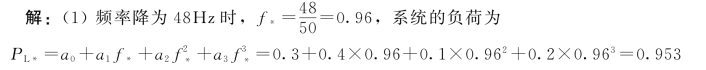
负荷变化为

其百分值为

此时，负荷的调节效应系数为

相应地，负荷变化为

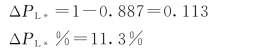
此时，负荷的调节效应系数为