牛顿-拉夫逊潮流计算原理及应用

1.牛顿-拉夫逊迭代计算原理

牛顿-拉夫逊是将非线性方程的求解过程转化为线性方程的求解过程，即线性化，是解非线性方程的一种有效方法，它的主要优点是收敛性较好，在一般网络中，只需迭代5～8次即可达到所需要的精度。

设有一非线性方程f（x）＝0，给定初值解为x（0），它与真解x之间的误差为Δx（0），因此，方程的真解可表示为

式中 Δx（0）——变量修正量。

应满足原方程方程式，故

将上式按泰勒级数展开为

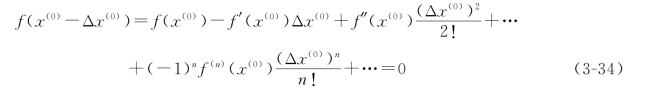
式中 f'（x（0）），f″（x（0）），…，f（n）（x（0））——函数f（x）在x（0）点的一阶、二阶……n阶导数。

如果所选择的初值较好，即Δx（0）很小时，可以将式（4-49）中Δx（0）的二次及二次以后各项忽略不计，则式（3-34）简化为

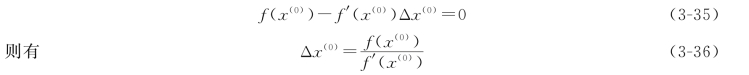
式（3-35）是Δx（0）的线性代数方程，称为牛顿—拉夫逊修正方程式，用它可以求出修正量Δx（0），见式（3-36）。由于式（3-36）是式（3-35）的简化结果，所以按式（3-36）计算出的Δx（0）只是近似值，还需要利用x（1）＝x（0）-Δx（0）对初值x（0）进行修正，这时的x（1）比x（0）向真解更逼近了一些。这时将x（1）作为初值带入修正式（3-35）中，得到

于是可以得到更逼近真解的公式x（2）＝x（1）-Δx（1）

牛顿-拉夫逊法的几何意义可用图3-15说明。函数f（x）＝0的真解在f（x）与x轴的交点x*处。任意假设的初值x（0）对应f（x）曲线的f（x（0）），f'（x（0））是函数在点x（0）的斜率，如图3-15所示。

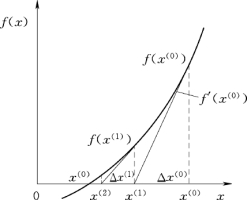
图3-15　牛顿-拉夫逊法的几何意义

修正量Δx（0）由点x（0）的切线与横轴的交点来决定。求得Δx（0）后，对x（0）进行修正，得

x（1）＝x（0）-Δx（0）。由图3-15可见，x（1）向函数的真解x*逼近一步。直到|x（v+1）-x（v）|＜ε，则称为迭代收敛。牛顿-拉夫逊法又称切线法。

下面将上述方法推广到n元方程组的情况。设有n元非线性方程组

将上述方程组中的方程在初值处分别展开为泰勒级数，并略去修正量的二次及以上高次项，可得

将式（3-39）改为矩阵形式，得

简写为

将式（3-40）、式（3-42）简写为如下的一般迭代形式

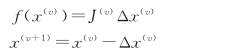
为了判断牛顿—拉夫逊法的收敛情况，采用以下不等式

运用牛顿法计算时，xi的初值要选择的比较接近真解，否则迭代过程可能不收敛。

2.牛顿-拉夫逊法潮流计算

（1）直角坐标形式。

以上介绍了牛顿-拉夫逊法迭代计算的基本原理，用此方法计算复杂系统的潮流只需把功率方程式变成迭代方程式的形式。下面仅对直角坐标形式的牛顿-拉夫逊法作详细介绍。

将式（3-30）功率方程式改写为功率误差的形式，则

上式对应于PQ节点的功率平衡方程式。

对应于PV节点，其有功功率是已知的，而无功功率未知，但节点电压给定，因此有

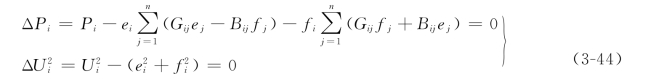
对于平衡节点，由于其电压是给定的，不必参与迭代，故不必列出其方程。

设系统中有n个节点，其中1～m为PQ节点，m+1～n-1为PV节点，n为平衡节点。这样，全系统有m个式（3-43），有n-m+1个式（3-44），即共有2（n-1）个迭代方程。给定一组初值，并将上述2（n-1）个方程按泰勒级数展开，略去Δei、Δfi的二次及以后各项，可得修正方程式(www.xing528.com)

上式中雅可比矩阵中各元素通过对式（3-43）和式（3-44）求偏导得到。

当j≠i时，雅可比矩阵各非对角元素分别为

当j＝i时，雅可比矩阵对角元素为

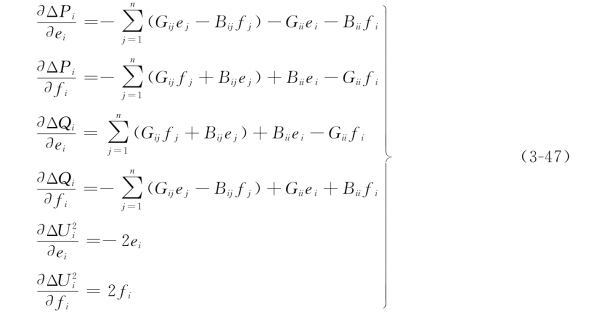
直角坐标形式的牛顿-拉夫逊法潮流计算过程及框图如图3-16所示。

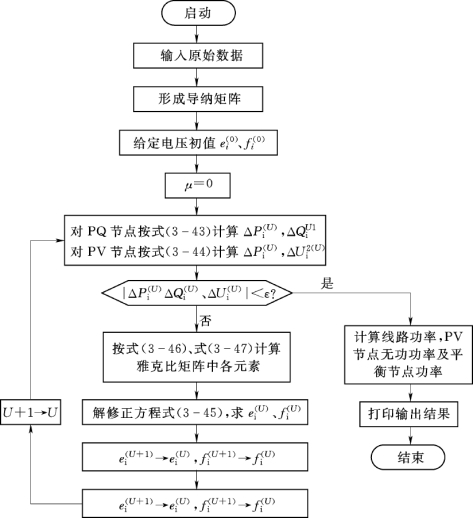
图3-16　牛顿-拉夫逊法潮流计算程序图

1）节点1，2的类型。

2）网络的节点导纳矩阵。

3）给定初值，用直角坐标形式的牛顿—拉夫逊作一次潮流迭代。

解：1）由已知条件可看出，节点1的电压和相位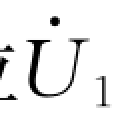＝1∠0°已知，故节点1位平衡节点。由于接点2的电压幅值U2＝1，节点2的有功功率P2＝PG2-PLD2＝15-20＝-5，故节点2为PV节点。

2）由上图可直接写出导纳矩阵。

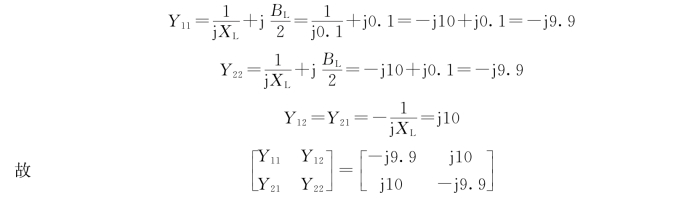
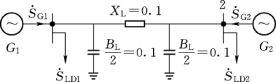
图3-17　［例3-4］图

3）写出功率误差方程式和电压误差方程式。

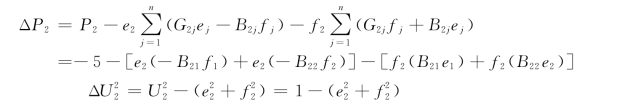
修正方程式为

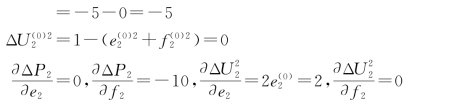
修正方程式为

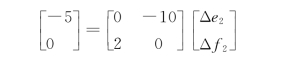
解得 Δf2＝0.5，Δe2＝0

（2）支路功率和平衡节点功率。

当计算收敛后，可得到各个节点的电压值，根据各节点的电压可以很方便地求出系统中各支路及变压器中流过的功率。

设线路或变压器的∏形等值电路如图3-18所示，支路导纳及支路对地导纳均标注在图中。若支路两端i、j的电压分别为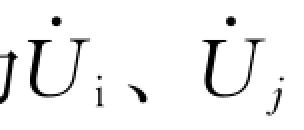，节点i、j注入的电流分别为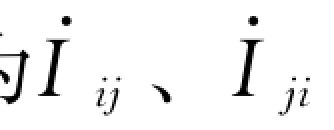，则支路功率为

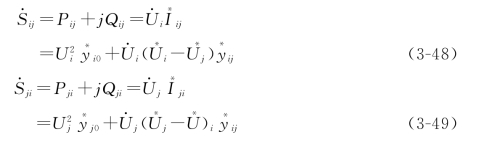
支路上的功率损耗为

平衡节点功率为

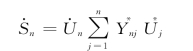
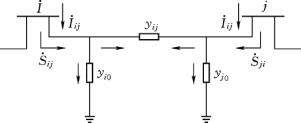
图3-18　∏形等值电路中流过的电流和功率

PV节点的无功功率Qi（i＝m+1，…，n-1）可以通过式（3-31）中的第二式求得。

（3）潮流计算中的约束条件

在潮流计算中还必须对某些控制变量和状态变量根据实际情况进行限制，否则最终结果有可能是实际工程所不能接受的。因此，潮流计算的解除了满足功率方程外，还必须满足如下约束条件。

对控制变量的约束条件为

上二式中 PGimin、PGimax、QGimin、QGimax——发电机和无功补偿设备的功率极限值。

对状态变量的约束条件为