误差检验结果的有效数据处理

在食品检验中，误差是客观存在的，因此，有必要先了解试验过程中误差产生的原因及误差出现的规律。

1.误差的分类

试验误差是指测定结果与真实值之间的差值，根据误差产生的原因与性质，误差可以分为系统误差和偶然误差两类。

（1）系统误差 系统误差是指在分析过程中由于某些固定的原因所造成的误差，具有单向性和重现性。根据系统误差的性质及产生的原因，系统误差可分为：

1）方法误差：由于实验方法本身不够完善而引起的误差，例如：在质量分析中，由于沉淀溶解损失而产生的误差；在滴定分析中，化学反应不完全、指示剂选择不当以及干扰离子的影响等原因而造成的误差。

2）仪器误差：仪器本身的缺陷所造成的误差，如天平两臂长度不相等，砝码、滴定管、容量瓶等未经过校正而引起的误差。

3）试剂误差：试剂不纯、蒸馏水中有被测物质或干扰物质所造成的误差。

4）个人误差：个人误差是指由于操作人员的个人主观原因造成的误差。例如，个人对颜色的敏感程度不同，在辨别滴定终点颜色时，偏深或偏浅等都会引起误差。

（2）偶然误差 偶然误差是指在分析过程中由于某些偶然的原因所造成的误差，也叫作随机误差或不可定误差。通常是测量条件（如试验室温度、湿度或电压波动等）有变动而得不到控制，使某次测量值异于正常值。偶然误差的特征是大小和正负都不固定，在操作中不能完全避免。

除了会产生上述两类误差外，往往还可能由于工作上的粗心、不遵守操作规程等而造成过失误差，例如：器皿不干净、丢失试液、加错试剂、看错砝码、记录及计算错误等，这些都属于不应有的过失，会对试验结果带来严重的影响，必须注意避免。

2.误差的表示方法

（1）准确度与误差 准确度表示分析结果与真实值接近的程度。准确度的大小，用绝对误差或相对误差表示。若以x表示测量值，以μ代表真实值，则绝对误差和相对误差的表示方法如下：

同样的绝对误差，当被测定物的质量较大时，相对误差就比较小，测定的准确度就比较高。因此用相对误差来表示各种情况下测定结果的准确度更为确切些。

绝对误差和相对误差都有正值和负值。正值表示试验结果偏高，负值表示试验结果偏低。

（2）精密度与偏差 对于不知道真实值的场合，可以用偏差的大小来衡量测定结果的好坏。偏差是指测定值x_i与测定的平均值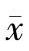之差，它可以用来衡量测定结果的精密度。精密度是指在同一条件下，对同一样品进行多次重复测定时各测定值相互接近的程度，偏差越小，说明测定的精密度越高。

精密度可以用绝对偏差、相对平均偏差、标准偏差与相对标准偏差来表示。

1）绝对偏差和平均偏差：测量值与平均值之差称为绝对偏差。绝对偏差越大，精密度越低。若令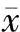代表一组平行测定的平均值，则单个测量值x_i的绝对偏差d为

d值有正有负。各单个偏差绝对值的平均值称为平均偏差，即

其中n表示测量次数。

2）相对平均偏差：平均偏差在平均值中所占的百分率称为相对平均偏差，即

3）标准偏差：使用标准偏差是为了突出较大偏差的存在对测量结果的影响，其计算公式为

4）相对标准偏差又称为变异系数，其计算公式为

5）最大相对偏差：

①相对偏差：用来表示测定结果的精密度，根据分析工作的要求不同而制定的最大值（也称为允许差）。(www.xing528.com)

②误差限度：指根据生产需要和实际情况，通过大量实践而制定的测定结果的最大允许相对偏差。

③相对相差：两次测定的结果之差占其平均值的百分率。

3.误差的减免

（1）选择恰当的分析方法 首先需要了解不同方法的灵敏度和准确度。根据分析对象、样品情况及对分析结果的要求，选择适当的分析方法。

（2）减小测量误差 为了保证分析结果的准确度，必须尽量减小各步骤的测量误差。一般分析天平的取样量要大于0.2g，滴定应消耗标准溶液的体积要大于20mL。

（3）增加平行测定次数 偶然误差的出现服从统计规律，即大偶然误差出现的概率小，小偶然误差出现的概率大；绝对值相等的正、负偶然误差出现的概率大体相等；多次平行测定结果的平均值趋向于真实值。因此在消除了系统误差的情况下，增加平行测定次数，可以减少偶然误差对分析结果的影响。

（4）消除测量中的系统误差

1）方法校正：有些方法误差可以用其他方法进行校正。例如，质量分析法中未完全沉淀出来的被测组分可以用其他方法（通常用仪器分析）测出，这个测出结果加入质量分析结果内，即可得到可靠的分析结果。

2）校准仪器：如对砝码、移液管、滴定管及分析仪器等进行校准，可以减免系统误差。

3）对照试验：用含量已知的标准试样或纯物质，以同一方法对其进行定量分析，由分析结果与已知含量的差值，求出分析结果的系统误差。以此误差对实际样品的定量结果进行校正，便可减免系统误差。

4）空白试验：在不加样品的情况下，用测定样品相同的方法、步骤进行定量分析，把所得结果作为空白值，从样品的分析结果中扣除。这样可以消除由于试剂不纯或溶剂等干扰造成的系统误差。

4.定量分析结果的数据处理

为了得到准确的分析结果，不仅要准确地测量而且还要正确地记录和计算数据。

（1）有效数字及运算规则

1）有效数字：在分析工作中实际能测量到的数字称为有效数字。在记录有效数字时，规定只允许数的末位欠准，可有±1的误差。

2）有效数字修约规则：用“四舍六入五成双”规则舍去过多的数字。即当尾数小于或等于4时，则舍；尾数大于或等于6时，则入；尾数等于5时，若5前面为偶数则舍，为奇数时则入；当5后面还有不是零的任何数时，无论5前面是偶或奇皆入。

3）有效数字运算法则：在加减法运算中，每数及它们的和或差的有效数字的保留，以小数点后面有效数字位数最少的为标准。在加减法中，因是各数值绝对误差的传递，所以结果的绝对误差必须与各数中绝对误差最大的那个相当。

在乘除法运算中，每数及它们的积或商的有效数字的保留，以每数中有效数字位数最少的为标准。在乘除法中，因是各数值相对误差的传递，所以结果的相对误差必须与各数中相对误差最大的那个相当。

（2）可疑值的取舍 在一组平行测定数值中，常发现有个别测定值比其余测定值明显偏大或偏小，这种明显偏大或偏小的数值称为可疑值。如查明的确是由于“过失”原因造成，则这一数据必须舍去；如果不能确定是由“过失”引起，则不能随便舍去或轻易保留，特别是当测量数据较少时，可疑值的取舍对分析结果产生很大的影响，必须慎重对待。可借助于统计学方法来决定取舍。统计检验方法有多种，各有其优缺点，比较简单的处理方法有Q检验法和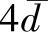法。

1）Q检验法：Q检验法又叫作舍弃商法。它是将多次测定的数据，按其数据的大小顺序排列为：x₁，x₂，…，x_n，设x_n或x₁为可疑值，根据统计量Q进行判断，确定可疑值的取舍。统计量Q为

式中分子为可疑值与相邻的一个数值之差，分母为整组数据的极差。Q值越大，说明可疑值偏离其他值越远。Q称为舍弃商，将Q_计值与Q_理论值比较，若Q_计值大则应舍弃可疑值，否则应保留。

2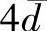）法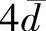：法是先求出除可疑值外的其余数据的算术平均值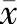及平均偏差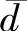，然后，将可疑值与平均值之差的绝对值与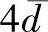比较，若其绝对值大于或等于，则可疑值应舍弃，否则应保留。

Q检验法符合数理统计原理，比较严谨，方法也简便，置信度可达90%以上，适用于测定3～10次的数据处理。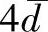法计算简单，不必查表，但数据统计处理不够严密，适用于处理一些要求不高的试验数据。