网络编码：提升数据传输效率的利器

2.1.2.1　网络编码原理

用无环图G=（V，E）表示一个网络，其中，V表示网络中节点的集合，E表示网络中边的集合，两个节点间可以存在多条链路，也就是多重图。为了表述方便，本书规定网络中每条链路的容量为1。

在单信源网络中，用s表示信源节点。对于某个节点a，其输入链路表示为In（a），其输出链路表示为Out（a）。节点a输入链路的个数表示为|In（a）|，输出链路的个数表示为|Out（a）|。对于单信源网络而言，源节点s是没有输入链路的，因此，In（s）表示节点s的虚拟输入链路，并且虚拟链路的数量与节点s单次发送数据包的数量相关，表示为N。信源节点s发送的消息表示为

其中，N表示数据包的数量，它比网络的最大流值小。经过网络编码后，网络信道上传输的数据表示为。

在网络编码中，对数据包而言，有两个重要的参数：局部网络编码和全局网络编码。

局部网络编码 若F为有限域，n为正整数，那么对于有向无环网络中的节点a和链路e∈Out（a），存在F域上的n维局部网络编码向量：

网络为有向无环网络，可以定义唯一的从上到下的秩序网络拓扑的顺序决定了编码顺序，节点按照编码顺序进行编码。

全局网络编码 若F是一个有限域，n为正整数，对于有向无环网络中的链路e，存在F域上的n维网络编码，该网络编码满足下述两个条件：

①对网络中的节点a和所有的传输链路e∈Out（a），c∈In（a），被唯一地确定，其对应的映射关系为：

②对于源节点s，有n个虚拟信道表示空间Fn到n个基坐标的投影。

2.1.2.2　随机网络编码

网络编码根据编码系数选取方式的不同，可以分为确定性网络编码和随机网络编码两种。确定性网络编码要求知道网络拓扑结构，即网络拓扑结构已知。确定性网络编码的对应编码系数不变，目的节点能正确解码以获取源节点发送消息，同时，它不需要传输全局编码向量。这是由于在拓扑结构已知的情况下，可以统一对链路的全局编码向量进行分配。但是，在实际的网络环境中，想要知道网络的拓扑结构是不可能的，尤其对于无线网络。对于这种网络环境，可采用随机网络编码。

在随机网络编码中，编码系数随机从一个足够大的有限域中选取，并使用选取的编码系数对数据包进行线性组合，目的节点在收到编码数据包后，采用高斯消元法解线性方程组进行译码，最后得到源节点发送的原始消息。

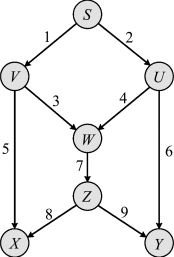
接下来以经典的蝴蝶型网络拓扑结构为例，阐述随机网络编码的原理。

在图2-2中，节点S表示信源节点，其发送的消息为x1和x2。对于目的节点X和Y而言，它们需要的消息就是源消息x1和x2。

(www.xing528.com)

图2-2　随机网络编码图示

该编码过程如下：链路1～9的编码系数（α1，α1，…，αn）是在有限域F上随机选取的。每条链路上处理的信息和编码系数都需要传输给下一跳节点。如信源节点S将C1=α1 x1+α2 x2和编码系数α1和α2通过链路1传输给节点V，同时将C2=α3 x1+α4 x2和编码系数α3和α4通过链路2传输给节点U。节点V将C1通过链路3和5分别传输给节点W和X；同样，节点U将C2通过链路4和6分别传输给节点W和Y。中继节点W在收到编码消息C1和C2后，对其进行编码，得到新的编码消息：

然后，节点W将编码C3和编码系数α5α1+α6α3和α5α2+α6α4发送给目的节点X和Y。目的节点在收到消息后，采用高斯消元法对编码消息进行解码。收到的编码消息包括：

当x1和x2的系数构成的系数矩阵满秩时，就可以解得消息x1和x2。这样，目的节点就能正确译码，从而得到源节点发送的源消息。

2.1.2.3　线性网络编码

根据网络上的节点对数据处理方式是否线性，将网络编码分为线性和非线性网络编码两种。从计算复杂度和构造难度来说，线性网络编码相对于非线性网络编码，计算量比较小，也更容易在实际应用中进行推广。

在线性网络编码中，网络编码对应的全局编码向量和局部编码向量都是线性的。其对应的编码矩阵描述如下：

局部编码矩阵 若F为一个伽罗华域，n表示正整数。针对有向无环网络中的节点a，它的编码矩阵可以表示为|In（a）|×|Out（a）|，即

其中，d∈In（a），e∈Out（a），kd，e为一个标量，它表示节点a的每一个相邻链路对（d，e）所对应编码系数。

全局编码矩阵 若F为伽罗华域，n为一个正整数。对于网络中的节点a，它对应的编码矩阵可以表示为Ka=[kd，e]。对于节点a的每一条输入链路d∈In（a）、输出链路e∈Out（a），它的编码向量fe和fd的关系如下所述：

根据上式，可以计算出网络中节点的全局编码向量。

信源节点S的虚拟链路的全局编码向量线性无关，并且其维数是n，从而组成Fn的基坐标。

对于目的节点t，其最大流不小于n，目的节点输入链路的全局编码向量构成n|In（t）|维的矩阵。并且在有限域F上存在矩阵D能译码，其维数为n|In（t）|，并且满足

其中，In表示n×n维单位矩阵。信宿t收到的消息为XT[fe]，解码时，用消息乘上矩阵D，那么XT[fe]D=XT（[fe]D）=XT In=XT，最终得到源消息。