数学基础：如何理解有向图中的顶点和边

2.1.1.1　图论基础概念

线图 假设V为顶点的集合，E为边的集合。如果∀e∈E，在集合V中都有一个顶点对（v，u）和边相对应，那么称集合V和集合E组成的图为一个线图，并表示为G=（V，E）。顶点u和v成为边e的两个端点，顶点v，u和边e彼此关联。

如果顶点集合V中一个顶点与边集合E中的任何边都不关联，那么该顶点为孤立点。如果线图中所有的顶点对（v，u）都为有序，那么该线图为有向图；否则，该线图为无向图。如果顶点集合V和边集合E都是有限集，那么线图G为有限图。如果顶点v和u相同，那么与它对应的边e表示自回路。

在线图G中，顶点v的度数与它相关联边的个数相等，表示为d（v）。在有向图中，对于任一顶点v，箭头指向v的边的数量表示顶点v的入度，表示为dIn（v）；箭尾为顶点v的边的数量称为顶点v的出度，表示为dOut（v），那么，对于顶点v，则有d（v）=dIn（v）+dOut（v）。如图2-1，以五个顶点为例，线图G=（V，E）表示如下：

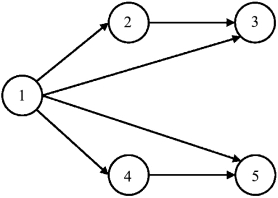
图2-1　有向图表示图

对应的顶点集合V={1，2，3，4，5}，边的集合E={（1，2），（1，3），（1，4），（1，5），（2，3），（4，5）}。边集中的每条边都是有方向的。顶点1的入度dIn（1）=0，出度dOut（1）=4；顶点5的入度dIn（5）=2，出度dOut（5）=0。该图没有孤立点，而且也没有回路。

2.1.1.2　网络基础概念

如果一个有向图满足下面的三个条件，那么该有向图称为一个网络：

①有一个或几个入度为0的顶点，该顶点称为信源。信源的集合表示为S；

②有一个或几个出度为0的顶点，该顶点称为信宿。信宿的集合表示为T；(www.xing528.com)

③图中的有向边＜u，v＞的权值为一个不小于0的整数，该整数为有向边＜u，v＞的容量，表示为Cuv。

如果网络G中只有一个信源节点，有一个或多个信宿节点，那么该网络为单信源网络。

可行流 一个网络G=（V，E，S，T，C）上的可行流f必须满足如下的条件：

①流量条件：对于中继节点V，所有入边的流量之和与出边流量之和相等。也就是：fIn（v）=fOut（v），其中，fIn（v）为入边流量之和，fOut（v）为出边流量之和。

②容量条件：对于任何边e∈E，0≤f（e）≤Ce。

最大流 假设f表示网络G=（V，E，S，T，C）上的一个可行流，如果fIn（T）=fOut（S），那么称fIn（T）或者fOut（S）为可行流f的流量，表示为Val（f）。网络G中流量的最大可行流则为网络的最大流。

割 给定一个网络G=（V，E，S，T，C），顶点集合M⊂V，M的补集，那么。当S⊂M时，（M，M ）为网络G的一个割。（M，M）的容量是割边上的容量之和，表示为。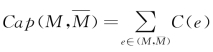

最小割 若网络G中的一个割称为网络G中的最小割，那么它必须满足下述条件：对于任一K＇为网络G的割，有Cap（K＇）≥Cap（K）。

最大流最小割 任一网络G=（V，E，S，T，C），其最大流流量值等于最小割的容量值，也就是Val（f*）=Cap（k*），其中，k*表示网络G的最小割，f*表示网络G的最大流。