《费克定律及扩散系数的影响因素》

在金属和合金中进行的过程，如再结晶、结晶、相变和组织结构变化、表面渗入其他元素都具有元素的原子扩散性质。

扩散可以理解为原子在晶体中移动超过该物质平均原子间距的距离。在一定体积内；如果原子移动不会引起浓度（化学成分）的变化，此过程被称为自扩散。

在合金或含有较多夹杂物的金属中的扩散伴随有浓度的变化被称做扩散或异扩散。

晶体中的扩散过程是原子机制、每个原子或多或少都完成一种偶然的“游移”，即在晶体点阵的平衡状态间形成一连串的跳动。任何一种原子扩散理论都始于对扩散机制的探讨，首先要回答的是该原子是如何从一个位置移向另一个位置的。

为了描述固态晶体（金属）的扩散过程提出了若干个可能的扩散机制：循环的、整体的、空位的和间隙的。

扩散速度是以单位时间通过单位界面扩散出的物质量来衡量的。单位时间内扩散出的物质量m取决于界面方向的元素浓度梯度dc/dx、正比于元素的扩散系数D，即

式中 dc——元素的浓度变化；

dx——已定方向上的距离。

此关系被称为费克（Fick）第一定律。式中的负号表示扩散方向是从浓度高的部分向浓度低的部分进行。如果浓度梯度依时间变化，则扩散过程可用费克第二定律来表征

推导此定律时，曾假定扩散系数与浓度无关，此假定只适合自扩散，故此方程只能在一定的扩散边界条件下求解。(www.xing528.com)

以高斯误差函数将此方程积分就得到一种抛物线规律，即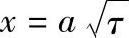，a是常数。由此可以对扩散系数给出直观的物理意义：如果把x视作原子平均扩散位移，就能把扩散系数近似地表示为x²=2Dτ、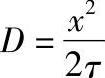。抛物线关系经常可以印证过程按扩散机制进行。扩散系数D的单位是cm²/s，也就是元素浓度降量等于1时，在单位时间（1s）通过单位面积（1cm²）扩散的物质量，和合金的本质、晶粒度、特别是温度有密切关系。扩散系数和温度的关系遵从指数规律

D=D₀exp[-Q/RT]

式中 D₀——指数前置因子，其数值取决于晶体点

阵类型；

R——玻耳茨曼常数，R=8.31J/（K·mol）；

T——热力学温度（K）；

Q——激活能（J/mol）。

为使原子完成一个最小的扩散步骤，它必须克服一定的能垒。原子的平均热能显著小于其从一个平衡位置移到另一位置为克服能垒所需的激活能Q。这种转移所需的富余能量取自相邻原子动能的不断交换。由于激活能Q在方程的幂指数中，故对扩散系数有很大影响。

沿表面和晶界的扩散最易进行，因为这些地方集中有大量晶体缺陷（空位、位错）。在晶粒（晶块）边界的扩散激活能比晶内几乎小一倍。