晶体中的原子扩散：2.5晶体中的新探索

（1）扩散与自扩散 晶体内原子的迁移超过该物质的平均原子间距。如果原子的迁移不改变各部分体积内的浓度，此过程被称为自扩散。金属和合金的许多过程（结晶、相变和组织转变、再结晶、表面渗入其他成分）都具有扩散特性。

（2）扩散与异扩散 在含较多杂质的金属和合金中发生伴随有浓度变化的扩散。

（3）扩散机制 笼统地说扩散是一种原子运动机制。物质中的每个原子都或多或少地进行着随机活动，即围绕点阵中各平衡位置作若干跃迁。任何一种扩散的原子理论都开端于扩散机制的研究。主要的原子扩散机制有循环机制、置换机制、空位机制和节（点）间机制，见图2-13。

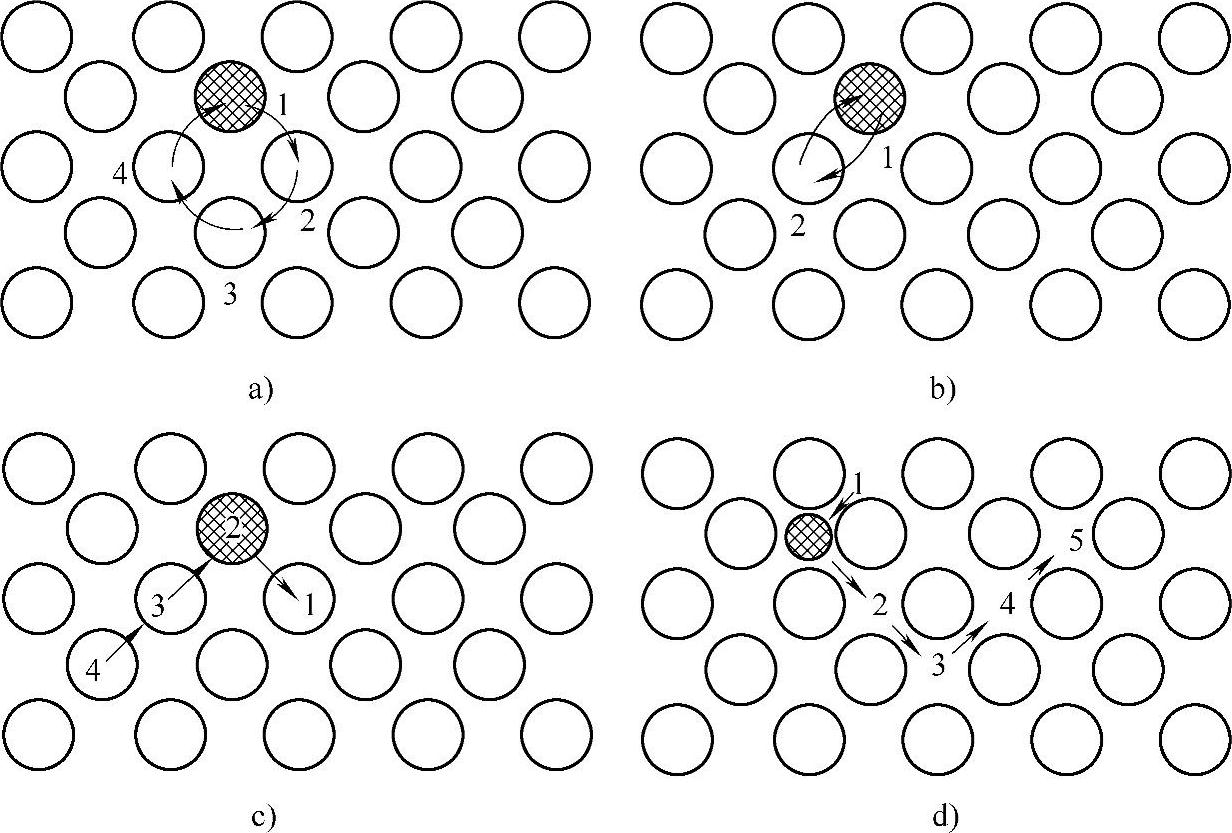
图2-13 扩散机制示意

a）循环机制 b）置换机制 c）空位机制 d）节点间机制

注：数字表示原子移动顺序。

（4）循环机制 一簇原子（如图2-13a中的4个原子）同时作环状旋转迁移，这种旋转不需要很大能量，但发生的几率很小。

（5）置换机制 相邻原子的相互置换，是循环机制的一种特殊情况（见图2-13b）。

（6）空位（穴）机制 从图2-13c可知，能位较高的原子2迁移到空穴位置。空穴转到原子2原先位置，也可能占据原子3的位置，如此类推。金属在金属中的扩散主要按空位机制进行。

（7）节（点）间机制 原子迁移到最近的节点间位置的平衡状态（见图2-13c）。原子半径小的元素，如C、N、H在金属中的扩散按节（点）间机制进行（见图2-13d）。

（8）扩散速率 单位时间通过单位界面面积扩散的物质量。

（9）费克第一定律 单位时间的扩散物质量m取决于垂直于界面方向的元素浓度梯度dc/dx，并和扩散系数D成正比：

m=-D（dc/dx）

式中 dc——浓度；(www.xing528.com)

dx——在选定方向上的距离。

式中负号表示扩散是从浓度大的区域向浓度小的区域进行，但在多元复杂合金中可能有逆扩散（上坡扩散），原子迁往浓度梯度增高的方向。这说明扩散驱动力通常不是浓度梯度，而是化学势梯度M；

M=L（dm/dx）

式中 L——决定化学势均衡的系数。

此外，如果物质自低浓度部分向高浓度区迁移能减小合金中的应力，也会出现逆扩散。

（10）费克第二定律 如果浓度梯度还依时间t而变化，则扩散过程由费克第二定律表述：dc/dx=D（d²c/dx²）。为推导此定律，要假设扩散系数与浓度无关，这只对自扩散是正确的。因此，必须在一定的扩散边界条件下才可解出此方程。可利用高斯误差函数将此方程积分，计算结果就是抛物线定律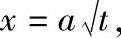a是常数。抛物线规律经常能表明一个过程符合扩散机制。

（11）扩散系数D在浓度差等于1时的单位时间（1s）通过单位面积（1cm²）扩散的物质量，其单位是cm²/s。该系数取决于合金的本质、晶粒大小，特别取决于温度。扩散系数的温度关系遵从指数规律：

D=D₀exp[-Q/（RT）]

式中 D₀——指数前因子，其数值取决于晶体点阵类型；

R——气体常数，等于8.31J/（K·mol）；

T——温度（K）；

Q——激活能（J/mol）。

（12）激活能 为了完成扩散的基本行为，一个原子必须要克服能垒。一个原子的热能显著小于从一个平衡位置迁移到另一平衡位置需要克服的能垒、即激活能。一个原子迁移所需的附加能量是通过原子间不断进行的动能交换方式取自相邻原子，因为原子的热运动具有各原子能量分布不均匀特征。由于激活能存在于指数中，故强烈影响扩散系数。在表面和晶界处的扩散是非常容易进行的，因为这些地方集中了晶体结构缺陷（空位、位错等），故晶界和亚晶块边界的扩散激活能要比晶内，即体扩散小一倍。