「PSS/E波形分析」——解读振荡模式数

上述这些方法的有效性将通过几个实例来进行展示，这些例子从简单的三模式线性系统到一个实际的电力系统。

1.简单例子

上述方法的应用将首先考察图7.3所示的波形，它是由下式得到的：

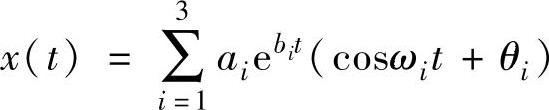
式中，

如果将此问题转化为只知道图7.3所示的波形，而不知道上述的解析表达式，那么应用Hilbert变换的第一步就是来估计此系统的振荡模式数。由Hilbert变换得到的频域响应如图7.4所示。从图7.4可以明显地看出，存在3个主导模式，分别位于4.7rad、8.0rad和17rad处，这与所给出的数据吻合得很好。

更进一步，3个模式的振幅分别为0.48、0.9和0.51，同样与所给出的数据能够较好吻合。如果每个振荡模式的自然振荡频率是分离的，并且脉冲响应频率是单独计算的，那么就可以确定每个振荡模式的阻尼。脉冲响应包络线的斜率可以用来估计各个振荡模式的阻尼比。在估计出每个模式的阻尼比后，就能计算出特征值。

下面将前面所述的3种方法中的任意一种用来估计图7.3信号的参数并重构波形。

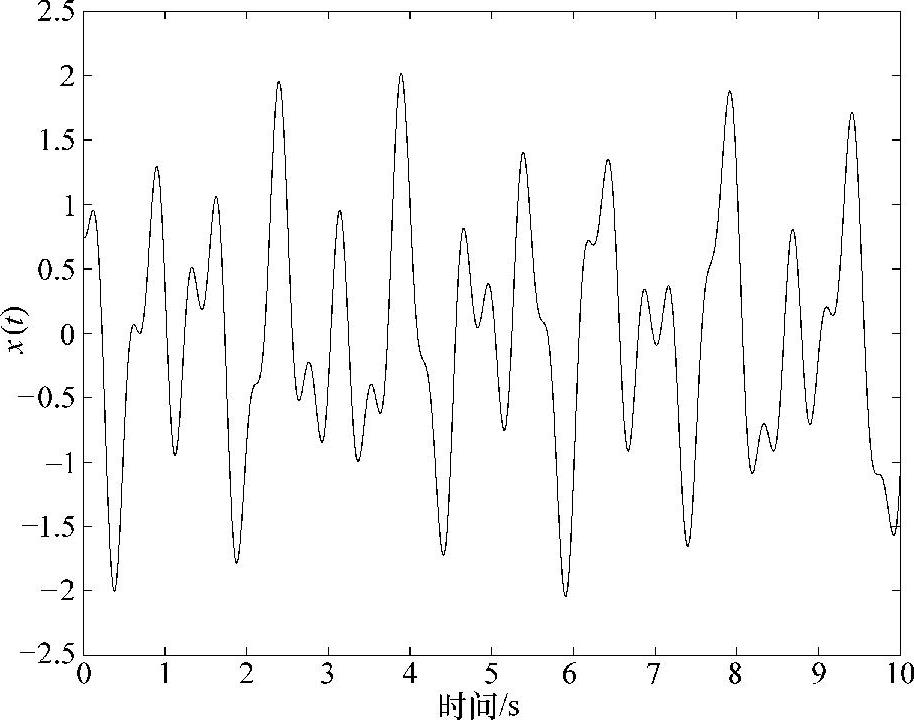
图7.3 3个振荡模式的波形

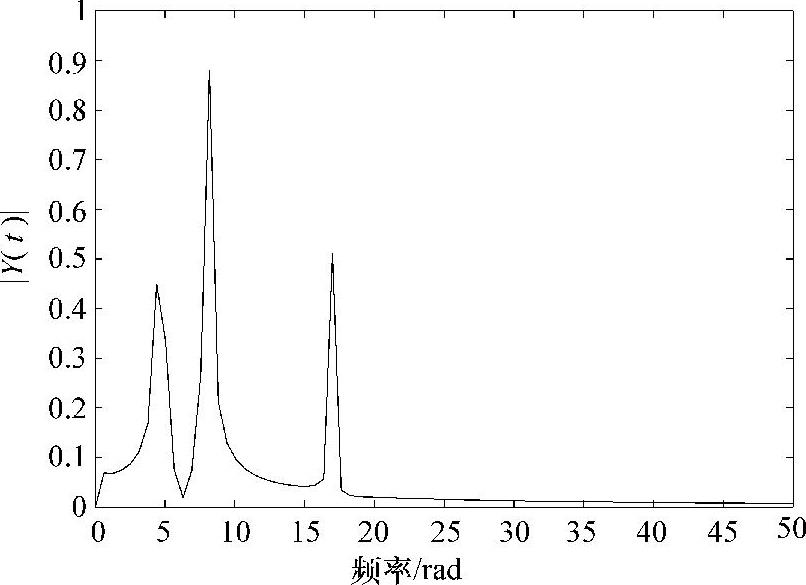
图7.4 图7.3的频域响应

Prony法：

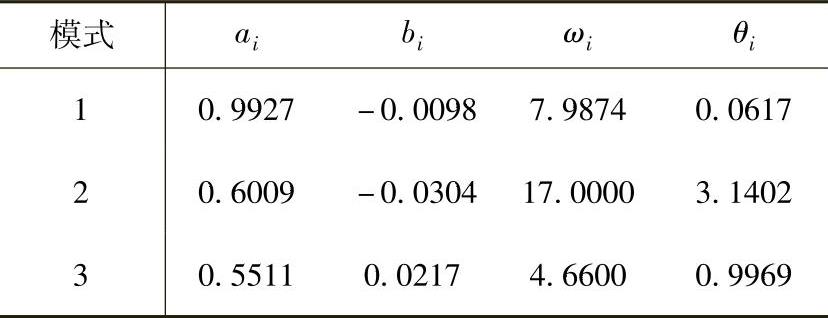
矩阵束法：

Levenberg-Marquardt法：

波形重构的误差（error）用下式计算：

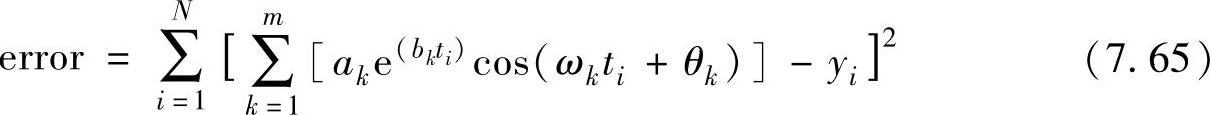
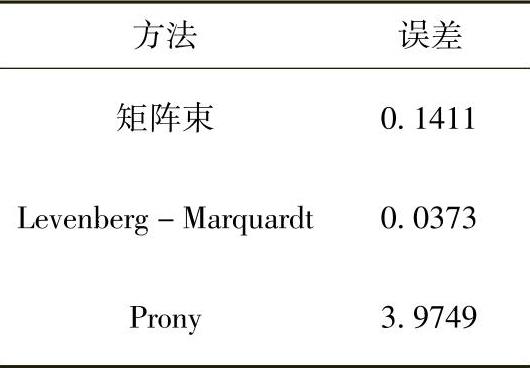
这样得到每种方法的重构误差为

(www.xing528.com)

果然Levenberg-Marquardt法得到了最好的结果，因为它是一种迭代方法，而其他的估计方法是线性非迭代方法。

2.电力系统例子

在这个例子中，将对前述几种方法的精度进行比较，所采用的动态响应曲线是基于PSS/E仿真美国中西部电网得到的，如图7.5所示。该系统包含了数百个状态，具有很宽频率范围的动态响应。该系统的主导振荡模式的个数是未知的。

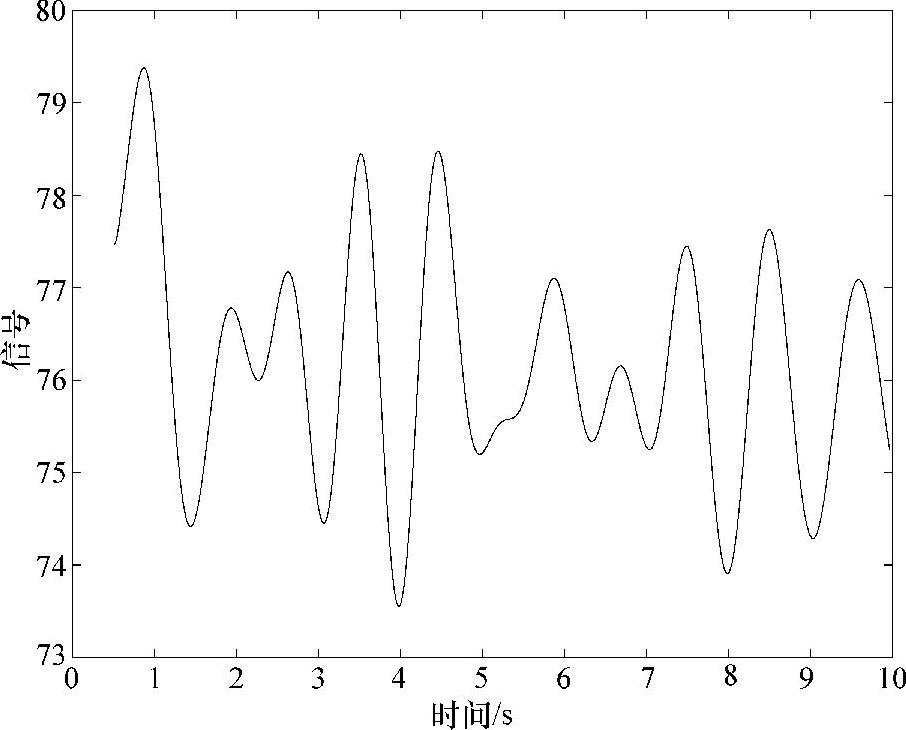
图7.5 PSS/E波形

首先使用Hilbert变换法来确定可能的振荡模式数，所得到的FFT结果如图7.6所示。从图中可以看出，似乎存在5个主导模式，对原始波形具有最大的贡献，且其中的几个集中在低频段。因此，前面讲述的几种估计方法将被用来提取5个振荡模式。

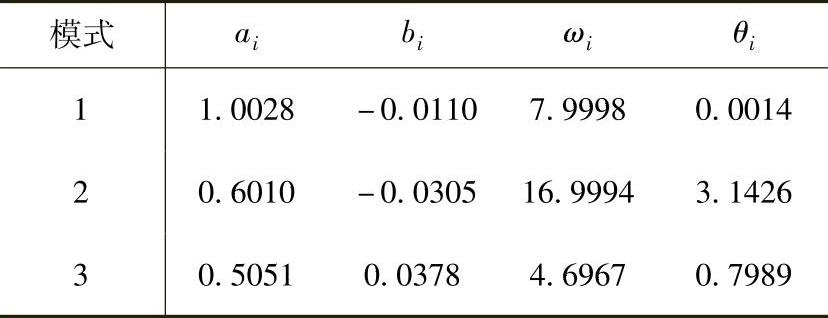
提取的5个振荡模式的结果如图7.7所示，3种方法的结果归纳如下：

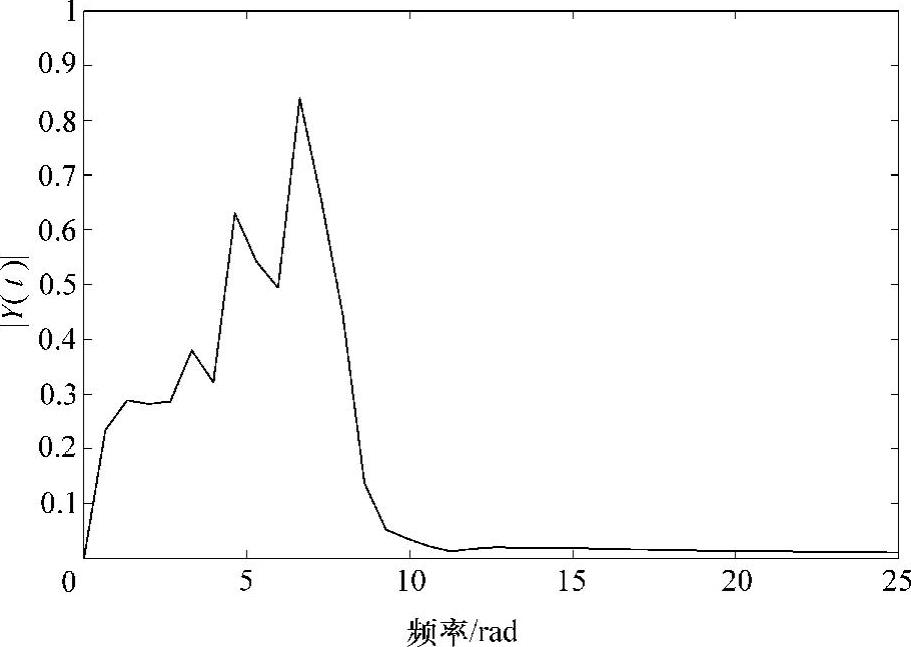
图7.6 PSS/E波形的FFT结果

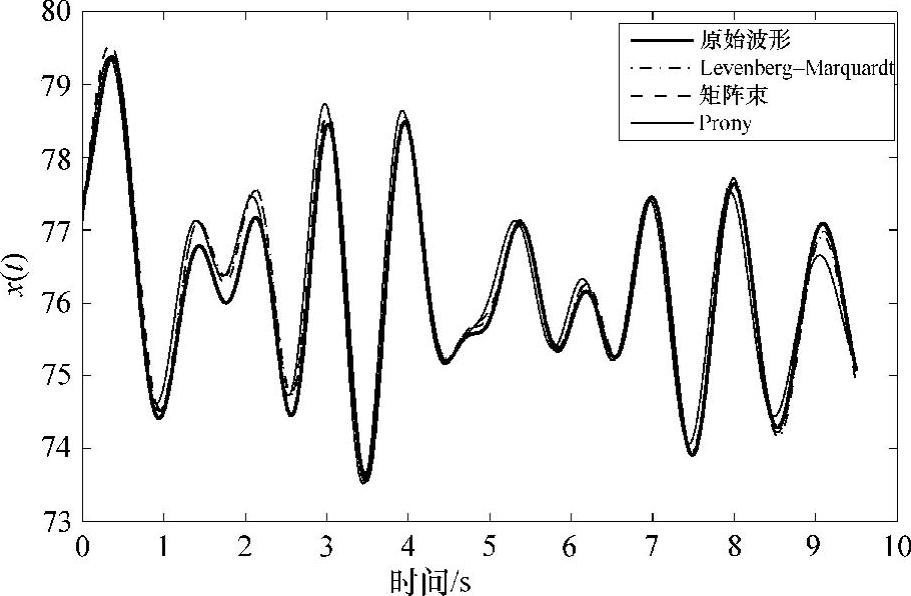
图7.7 使用不同方法得到的重构波形

Prony法：

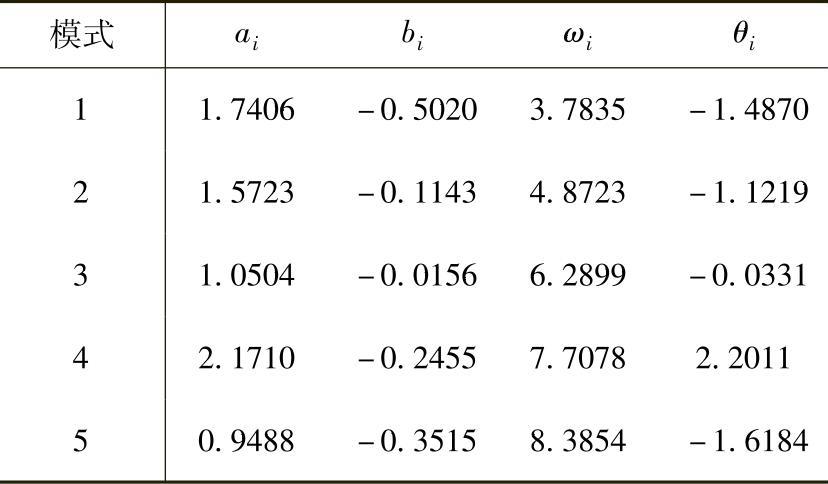
矩阵束法：

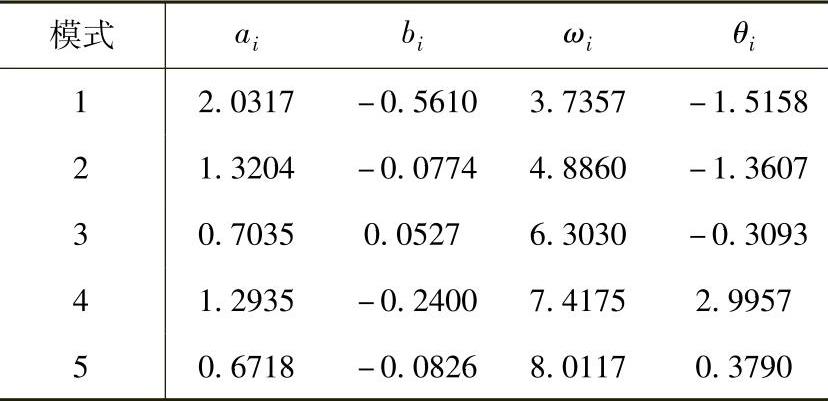
Levenberg-Marquardt法：

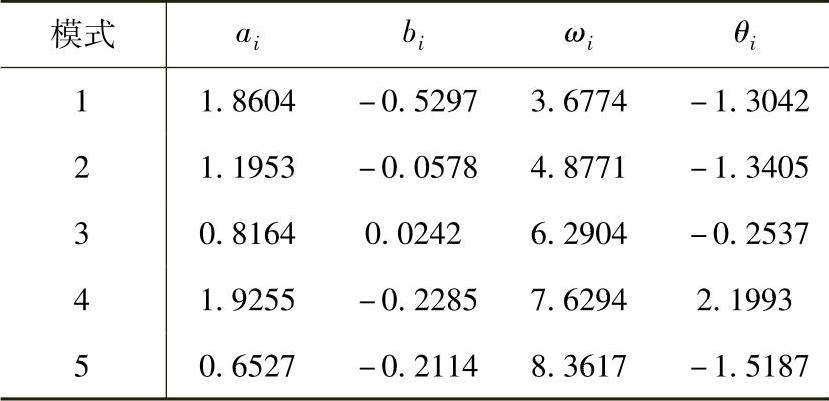
每种方法的误差由式（7.65）计算，3种方法的误差和计算时间如下表所示：

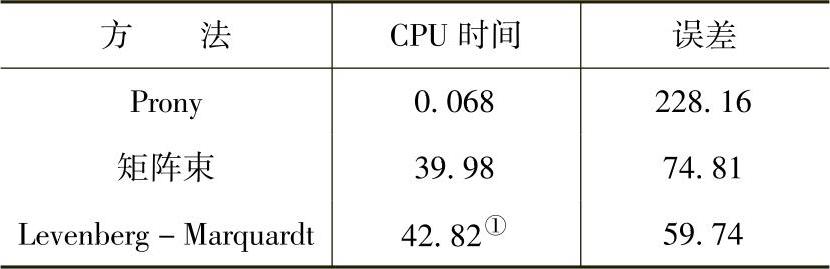
①根据初始条件。

注意，Prony法是计算效率最高的，因为它只需要2次最小二乘法求解。矩阵束法计算量较大，因为它需要对一个较大的矩阵进行1次奇异值分解；同时还需要对一个较小的矩阵（其阶数等于所求的模式数）进行特征值求解，不过这个计算并不过于繁重。毫不奇怪，Levenberg-Marquardt法是计算量最大的，因为它是一个迭代方法。该方法的计算量直接与初始值有关：初始值越好，收敛得越快。将Prony法或矩阵束法得到的参数作为Levenberg-Marquardt法的初始值是非常明智的做法。

类似地，每种方法的误差水平也随着方法的复杂程度而改变。Levenberg-Marquardt法能够得到最好的结果，但需要最长的计算时间。Prony法的误差最大，但计算速度最快。