Levenberg-Marquardt法详解

用于数据拟合的非线性最小二乘问题的一般形式为

式中，y_i是系统在t_i时刻的输出，x是式（7.34）中的振幅、相位、角频率和阻尼系数组成的向量，它取决于系统状态矩阵的特征值。

为了求出f（x）的最小值，可以采用Newton-Raphson迭代法的相同步骤。函数f（x）在某个x₀附近做Taylor级数展开：

式中，

如果忽略Taylor级数展开式中的高次项，并对式（7.53）右边的二次函数进行最小化，可以得到

x₁=x₀-[f″（x₀）]^-1f′（x₀） （7.54）

由此得到了求解函数f（x）最小值的一个近似公式。上式实际上是求解

f′（x）=0

的Newton-Raphson迭代更新式，而f′（x）=0是使f（x）最小化的必要条件方程。

Newton-Raphson迭代式（7.54）可以改写成如下的线性迭代形式

A（x_k）（x_k+1-x_k）=g（x_k） （7.55）

式中，

这里的矩阵A是系统的Jacobi矩阵（或类似的迭代矩阵）。

式（7.52）的导数为

而

在这种情况中，矩阵元素a_j，k包含了函数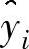的二阶导数。这些导数乘上系数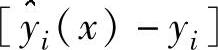后，在f的最小化过程中会变得越来越小。因此可以这么认为，在整个最小化过程中这些项可以忽略。注意，如果此方法收敛，那么不管迭代过程中Jacobi矩阵是否精确，都会收敛到同一个结果。因此迭代矩阵A可以简化为(www.xing528.com)

且注意其中的a_jj（x）>0。

Levenberg-Marquardt法通过引入矩阵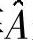来修改式（7.55），矩阵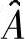的元素为

式中，γ是某个正的参数。这样式（7.55）变为

对于较大的γ，矩阵会变成对角占优矩阵。如果γ接近于0，式（7.57）会变成Newton-Raphson法。Levenberg-Marquardt法的基本特性就是通过选择不同的γ来获得最优的迭代特性。基本Levenberg-Marquardt法可以概括为

Levenberg-Marquardt法

1.令k=0。选择一个初始的x0、γ和系数α。

2.求解式（7.57）中的线性方程组，获得xk+1。

3.如果f（x_k+1）>f（x_k），x_k+1不能作为新的近似值，因此舍弃，并将γ用αγ替代，重复步骤2。

4.如果f（x_k+1）<f（x_k），接受x_k+1作为新的近似值，将γ用替代，令k=k+1，重复步骤2。

5.当下式满足时结束迭代

‖x_k+1-x_k‖<ε

针对非线性波形通过一系列函数进行拟合的问题，相应的最小化函数可用下式给出：

最小化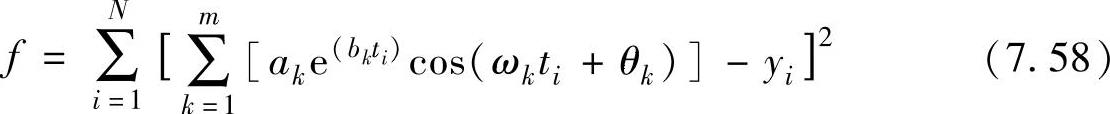

式中，m是待拟合波形的振荡模式个数，x=[a₁，b₁，ω₁，θ₁，…，a_m，b_m，ω_m，θ_m]^T。

与所有的非线性迭代法一样，Levenberg-Marquardt法能否收敛取决于初始值的选择。在这种情况下，采用矩阵束法或Prony法的结果作为初始值是明智的。