Prony法的理解和应用

Prony法是用来估计上述不同参数的一种方法^[23]，即直接估计拟合函数的各指数项参数，拟合函数的表达式为

被拟合的测量波形是y（t），由N个采样值构成

y（t_k）=y（k），k=0，1，…，N-1

这些采样值是等时间间隔分布的，时间间隔为Δt。由于测量信号y（t）可能包含噪声或直流偏置，因此可能需要在拟合过程开始前进行预处理。

基本的Prony法归纳如下。

Prony法

1.根据测量数据集构建一个离散的线性预测模型。

2.求出模型特征多项式的根。

3.使用这些根作为信号的复模态频率，确定每个振荡模式的振幅和相位。

上述步骤在z域中执行，并在最后一步将特征值转换到s域中。

注意，式（7.34）可以重新写成复指数形式：

上式可以转换成

式中，(www.xing528.com)

系统特征值λ可以通过下式从离散模式中得到：

而z_i是如下n次多项式的根：

zⁿ-（a₁z^n-1+a₂z^n-2+…+a_nz⁰）=0 （7.39）

式中，系数a_i是未知的，必须通过测量数据向量计算得到：

注意，这是一个具有n个未知数和N个方程的方程组，因此必须通过最小二乘法进行求解。

一旦z_i作为式（7.39）的根已求出，特征值λ_i就可以根据式（7.38）进行计算。下一步就是求解B_i，使其满足对所有的k都有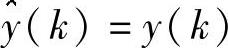。因而可以得到下面的关系式：

上式可以简洁地写成：

ZB=Y （7.42）

注意，矩阵B是N×n的；因此式（7.42）也必须采用最小二乘法求解。然后，根据式（7.35）就能计算出估计的波形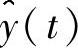。重构的信号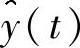通常不会与y（t）精确重合。对此种拟合质量的一种合适的度量是“信号噪声比（SNR）”，由下式给出：

式中，SNR的单位为分贝（dB）。

因为此种方法的拟合可能不够精确，通常希望控制拟合函数与原始波形之间的误差水平。在这种情况下，非线性最小二乘法可以给出更好的结果。