如何进行奇异值分解？

奇异值分解（SVD）产生3个矩阵，这3个矩阵的乘积等于矩阵A（可以不是方阵），即

A=UΣV^T （7.28）

式中，U满足U^TU=I，且U的列是AA^T的正交归一化特征向量；V满足V^TV=I，且V的列是A^TA的正交归一化特征向量；而Σ是一个对角矩阵，对角线元素包含了与U（或V）相对应的特征值的平方根，且按降序排列。

SVD既可以用QR法也可以用Arnoldi法实现，目的是求矩阵A^TA和AA^T的特征值和特征向量。一旦求出特征值，奇异值便是对应的平方根。矩阵的条件数是度量矩阵可逆性程度的一个指标，定义为该矩阵的最大奇异值与最小奇异值之比。条件数大意味着矩阵接近奇异。

例7.6 对A进行奇异值分解

解7.6 矩阵A是一个4×5矩阵，因此U是一个4×4矩阵，Σ是一个对角线上有4个奇异值且最后一列为0的4×5矩阵，而V是一个5×5矩阵。

首先令

得到

再用QR法计算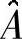的特征值和特征向量，得到

矩阵Σ的对角线元素是奇异值，等于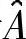的特征值的平方根，而且维度必然和A一样，因此有

类似地，令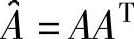重复上面步骤，可以得到U：

奇异值分解除了应用于条件数计算外，另一种常见的应用是求非方阵A的伪逆矩阵A⁺。最常见的伪逆矩阵是Moore-Penrose伪逆矩阵，这是一种被称为1-逆矩阵的一般性意义上的伪逆矩阵的一个特例。伪逆矩阵通常被用来求解最小二乘问题Ax=b，其中A是奇异矩阵或非方阵。根据6.1节的结果，最小二乘问题的解为

x=（A^TA）^-1Ab(www.xing528.com)

=A⁺b

矩阵A⁺可以通过LU分解得到，但更常用的方法是采用奇异值分解得到。若采用奇异值分解方法，伪逆矩阵由下式给出：

A⁺=VΣ⁺U^T （7.29）

式中，Σ⁺是一个和A^T具有相同维度的对角阵，且其对角线元素为奇异值的倒数。

例7.7 使用伪逆矩阵法求解例6.1。

解7.7 为方便起见，将该方程重新写出如下：

采用伪逆矩阵法求解

使用奇异值分解得

矩阵Σ⁺为

从而得到A+

结果与例6.1相同。