Arnoldi法：一种高效解法

对于大型互联系统，受计算机内存和计算速度的限制，求出系统状态矩阵的所有特征值，要么不可能，要么极其困难。Arnoldi法是用迭代方法计算n×n矩阵k个特征值的算法，这里的k比n小得多。因此这个方法绕过了很多大型矩阵运算所构成的障碍，而这些大型矩阵运算在诸如QR分解那样的算法中是不可避免的。如果k个特征值是经过挑选的，就可以提供丰富的关于待研系统的信息，而不一定需要得到所有的特征值。Arnoldi法最早是由参考文献[2]提出的，但存在诸如失去正交性和收敛速度慢等不良数值计算特性。对Arnoldi法的多种改进已克服了这些缺点。改进的Arnoldi法（MAM）已在电力系统相关的特征值计算中经常得到应用^[29，51]。这个方法引入了预处理和显式重启动技术来保持正交性。然而不幸的是，显式重启动经常会丢失有用信息。通过引入隐式移位QR分解过程，隐式重启动Arnoldi（IRA）法^[45]解决了上述显式重启动所存在的问题。围绕IRA法已开发出了多种商业软件包，其中包括著名的ARPACK软件包和Matlab的speig程序。

Arnoldi法的基本思路是通过迭代不断更新一个低阶的矩阵H，使H的特征值逐次逼近高阶矩阵A中已选定的特征值：

AV=VH；V^∗V=I （7.16）

式中，V是一个n×k矩阵；H是一个k×k的Hessenberg矩阵。随着此方法的展开，矩阵H的对角元将逼近A的特征值，有

HV_i=V_iD （7.17）

式中，V_i是一个k×k矩阵，它的列是矩阵H的特征向量（逼近A的特征向量），D是一个k×k矩阵，其对角元是矩阵H的特征值（逼近A的特征值）。Arnoldi法是一种正交投影到Krylov子空间上的方法。

Arnoldi法的计算过程是一种构造Krylov子空间正交基的过程。其中的一种做法如下：

k步Arnoldi分解算法

开始设定一个单位范数的向量v₁，对于j=1，…，k进行计算：

1.H（i，j）=v^T_iAV_j，i=1，…，j

2.

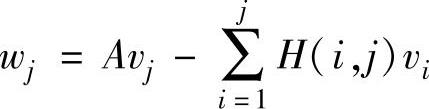
3.H（j+1，j）=‖w_j‖₂

4.当H（j+1，j）=0时，停止计算

5.

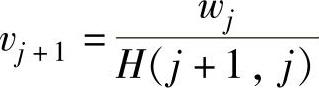
每一步，算法都用先前的Arnoldi向量v_j乘以A，然后对得到的向量w_j进行相对于先前所有v_i的正交归一化。k步Arnoldi分解的结果如图7.1所示，并可用下式表示：

AV_k=V_kH_k+w_ke^T_k （7.18）

式中，V=[v₁，v₂，…，v_k]的各列构成了Krylov子空间的一个正交归一化基，而H是A在这个子空间上的正交投影。期望‖w_k‖尽量小，因为这意味着H的特征值已精确逼近A的特征值。然而，这个收敛过程是以对V进行数值正交化为代价的。因此，k步Arnoldi分解需重新启动，以保持正交性。

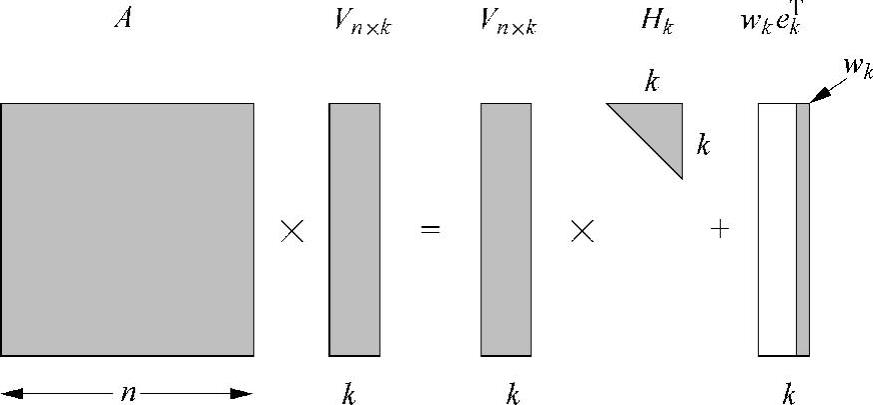
图7.1 k步Arnoldi分解的结果

隐式重启动过程提供了一种从很大的Krylov子空间中提取丰富信息的方法，并避免了标准方法中存在的存储问题和不良数值特性。这是通过使用移位QR法不停地将信息压缩到一个固定维数的k维子空间中来实现的。隐式重启动过程将（k+p）步Arnoldi分解

AV_k+p=V_k+pH_k+p+w_k+pe^T_k+p （7.19）

中的感兴趣的特征值信息压缩到长度为k的Arnoldi分解中。这是基于QR法并采用p次移位来实现的，其结果为

式中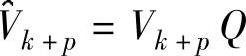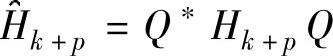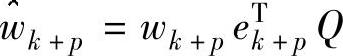，，，。可以证明，向量e^T_k+pQ的前k-1个元素为0^[46]。令上述等式两侧前面的k列相等，就得到一个更新了的k步Arnoldi分解，从而提供了将k步Arnoldi分解扩展为（k+p）步Arnoldi分解的重启动向量集。（k+p）步Arnoldi分解的结果如图7.2所示。

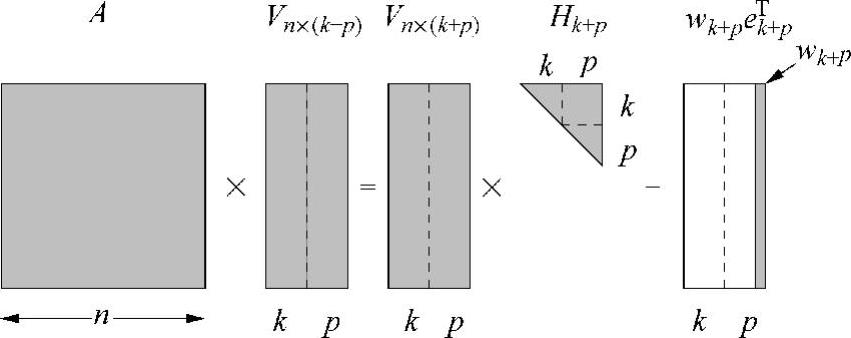
图7.2 （k+p）步Arnoldi分解的结果

隐式重启动Arnoldi法主要由三步组成：初始化；迭代和精细化；最终计算特征值和特征向量。

隐式重启动Arnoldi法

1.初始化

使用向量v₁作为启动向量，构造一个k步的Arnoldi分解。在此k步Arnoldi分解的每一步中，矩阵V都通过新求出的向量v扩展1列，但相互之间必须满足式（7.18）。注意，H_k是一个Hessenberg矩阵。图7.1中的阴影部分代表了非零元素，w_ke_k^T的非阴影部分是一个具有（k-1）列的零矩阵，w_ke_k^T的最后一列是w_k。此Arnoldi分解完全取决于初始向量v₁的选择。

2.迭代和精细化

（a）将k步Arnoldi分解扩展p步

新增的p个元素中的每一个都代表了在迭代结束后可以丢弃的特征值和特征向量，如果它不满足入选的标准的话。一般来说，p值的选择是在可容忍的分解长度与收敛速度之间进行折中。对于大多数问题，p值的选择通过实验性计算确定。对p的唯一要求是1≤p≤n-k。

（b）计算H_k+p的特征值

在完成了Arnoldi分解的p步扩展后，H_k+p的特征值可以通过QR法来计算，并根据预先确定的排序标准S从最好到最差进行排序。最差的p个特征值（σ₁，σ₂，…，σ_p）被用作移位值以实现p次移位QR分解。由于在Arnoldi分解式

AV_k+p=V_k+pH_k+p+w_k+pe^T_k+p （7.21）

中，矩阵H_k+p的阶数是相对较小的，因此可以高效地利用移位QR分解来计算H的特征值。

（c）更新Arnoldi矩阵

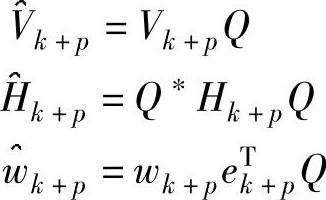
注意，更新后的矩阵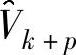具有正交的列，因为它是V与正交矩阵Q的乘积。

（d）获取新的k步Arnoldi分解

令式（7.20）两边的前k列相等并丢弃最后面的p个方程，就得到了一个新的k步Arnoldi分解式：

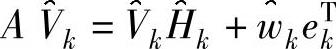
式中，向量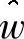是一个新的残差向量，会随着迭代和精细化步骤的不断重复而逐渐趋向于0。

（e）判断迭代和精细化步骤是否完成

如果

‖AV_k-V_kH_k‖≤ε

式中，ε是一个预先设定的收敛阈值，那么迭代和精细化步骤完成。否则，根据（d）的结果重新开始迭代和精细化步骤直到上式成立。

3.特征值和特征向量计算

Arnoldi法的最后一步是根据下式计算约简矩阵H_k的特征值和特征向量：

H_kV_k+V_hD_k （7.22）

然后计算A的特征向量为

V_k=V_kV_h （7.23）

所需的A的特征值可以从D_k的对角线元中获得

AV_k=V_kD_k （7.24）(www.xing528.com)

例7.5 使用一个3步Arnoldi分解，求例7.2矩阵的2个最小模特征值及对应的特征向量。

解7.5 因为所求的是2个最小模特征值，所以k的值是2。在初始化步骤之后，此2步Arnoldi法将扩展成3步Arnoldi法；因此，p等于1。因此，对于每一次迭代，将计算3个特征值，而最差的那个特征值将会被丢弃掉。

分解过程可以由任意一个非零向量启动。在很多软件中，启动向量是随机选取的，只要保证每个元素的绝对值小于0.5。本例的启动向量选为

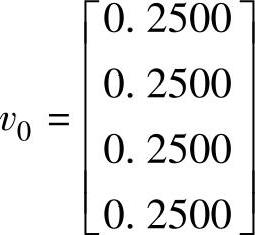
为了满足初始向量模值为1的要求，对启动向量进行归一化处理并产生初始向量v₁：

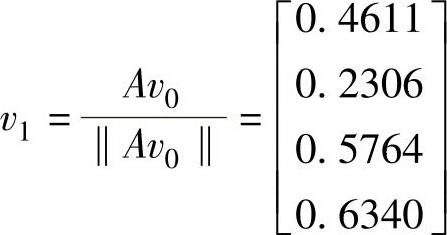
在初始向量选择完毕后，执行k步Arnoldi分解；因此，

h_2，1v₂=Av₁-h_1，1v₁ （7.25）

式中，v₂组成了V_k的第2列，h₁，1通过下式计算：

h_1，1=<v₁，Av₁>=v^T₁Av₁ （7.26）

式中，<·>表示内积。这样，由式（7.26）可得h_1，1=180.399。使用Arnoldi分解算法求w₁得

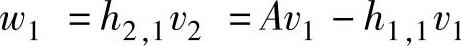
用h_2，1将v₂归一化，而h_2，1=0.3483，因此

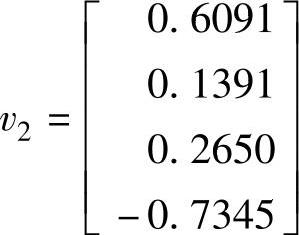
计算Hessenberg矩阵的剩余元素，可以得到

h_1，2=v₁^∗Av₂=0.1671

h_2，2=v₂^∗Av₂=-6.2370

继续使用Arnoldi分解算法求w₂得

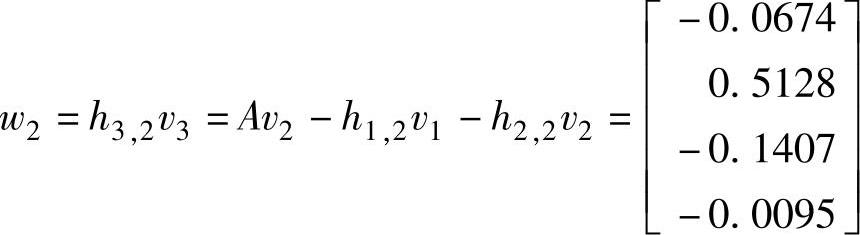
可以检查这些值，看是否满足k=2时的式（7.18）：

AV₂=V₂H₂+w₂[0 1]

式中，

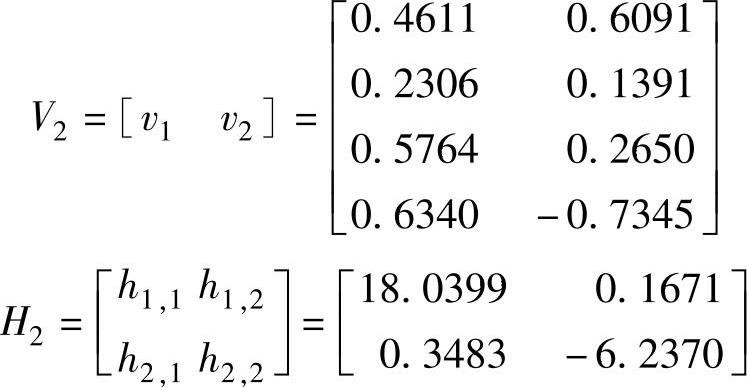
到此初始化步骤完成。

在完成初始的k步Arnoldi分解后，可以进一步扩展到k+p步Arnoldi分解。对于本例，p=1；所以只要扩展一步就可以了。在初始化过程中已经得到w₂=h_3，2v₃，据此可以提取出h_3，2和v₃（考虑到‖v₃‖=1.0），得到h_3，2=0.5361和

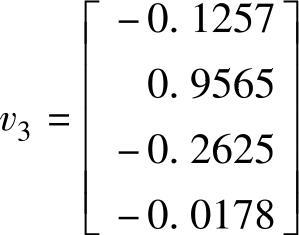
Hessenberg矩阵H₃为

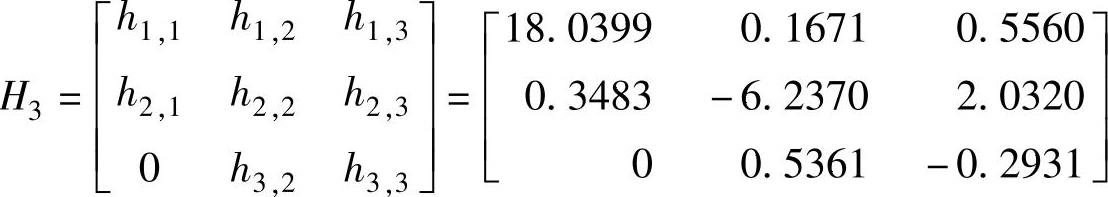
式中，

h_1，3=v^T₁Av₃

h_2，3=v₂^TAv₃

h_3，3=v₃^TAv₃

继续使用Arnoldi分解算法求w₃得

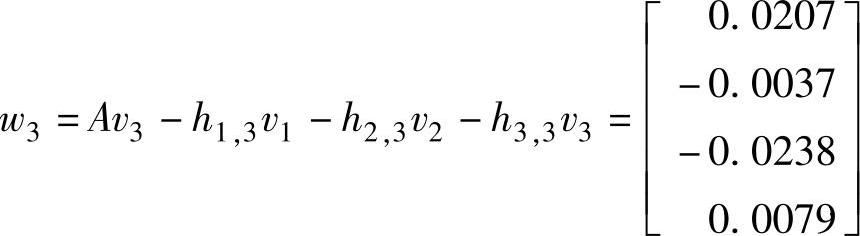
下一步是使用QR分解法计算小矩阵H₃的特征值（和特征向量），并对其进行排序。H₃的特征值为

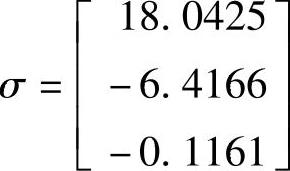
因为想求的是模最小的2个特征值，故特征值的排序方式是模最小的特征值排在最底部（上式已经是这么排了）。不想要的特征值的估计值是σ₁=18.0425。对H₃-σ₁I使用移位QR分解得到

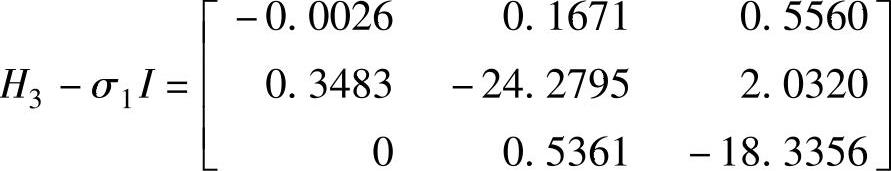
而

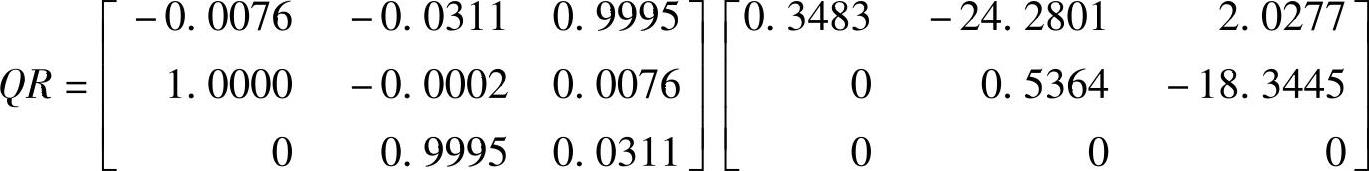
利用Q可以得到更新后的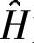为

注意，现在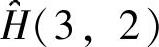已为0。继续计算过程得到更新的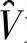为

式中，V₃=[v₁v₂v₃]，而

注意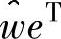，的第1列为0，所以一个新的2步Arnoldi分解可以通过使上式左右两边的前2列相等得到，即

而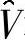和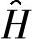的第3列被丢弃掉。

这个迭代与精细化过程直到满足下式时结束：

‖AV-VH‖=‖we^T‖<ε

此时，计算得到的特征值将具有ε精度。