幂法与反幂法的收敛速度及适用条件

幂法是求n×n矩阵A的主特征值的最常见方法之一。主特征值指的是绝对值最大的特征值。因此，如果λ₁，λ₂，…，λ_n是A的特征值，那么λ₁是A的主特征值，意味着对于所有的i=2，…，n，有

|λ₁|>|λ_i| （7.5）

幂法实际上是一种求与矩阵A的主特征值对应的特征向量v₁的方法。一旦特征向量确定，则对应的特征值便可以通过Rayleigh商提取出来：

求特征向量v₁的途径是采用迭代法。首先确定一个初始猜测向量v⁰，然后构造一系列的近似向量v^k，期望当k趋向于无穷时该序列能够收敛。幂法的迭代步骤是直接明了的。

幂法的迭代步骤：

1.令k=0并选择一个非零的n×1向量作为v⁰

2.w^k+1=Av^k

3.α_k+1=‖w^k+1‖

4.

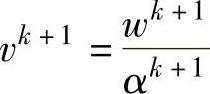
5.当满足‖v^k+1-v^k‖<ε时迭代结束。否则，k=k+1，跳到第2步

第4步中除以范数的运算并不是一个必需的步骤，但它保证了特征向量值的范围接近于1。考虑到一个标量乘上矩阵A的特征向量后仍然是矩阵A的特征向量，因此规格化并没有不良后果。然而，如果没有第4步使对所有的k都有α^k=1，那么更新后的向量的值可能会增加或减小到影响计算机精度的程度。

例7.1 使用幂法求如下矩阵与主特征值对应的特征向量：

解7.1 令初始猜测向量v⁰=[1 1]^T，则

α¹=‖w¹‖=6.4031

第2次迭代为(www.xing528.com)

α²=‖w²‖=9.0594

继续迭代得到收敛的特征向量：

根据此特征向量，可以计算出相应的特征值：

这正是矩阵A的最大特征值（最小特征值为0.2280）。

为了说明为什么幂法能够收敛到主特征向量，可以将初始猜测向量v⁰表示为如下的线性组合形式：

式中，v_i是A的实际特征向量，β_i是使式（7.7）成立的系数。然后使用幂法（不失一般性可以认为对所有k，α^k=1都成立）得到

因为

当k不断增大时，这些项会趋于0，只有与v₁对应的部分被保留下来。

当存在两个具有相同绝对值的最大特征值时，幂法就会失败。考虑到实矩阵A的特征值一般为复数并且以共轭对的形式存在（两者必然有相等的绝对值）。因此，如果A的最大特征值不是实数，那么幂法必然无法收敛。由于这个原因，只对已知其特征值为实数的矩阵使用幂法是明智的。在其特征值为实数的所有矩阵中，对称矩阵是其中的一类。

还存在一种情况，使用幂法无法收敛到主特征值对应的特征向量。这种情况会在β₁=0时发生。这意味着初始向量v⁰不包含特征向量v₁。在这种情况下，幂法会收敛到与绝对值第二大的特征值所对应的特征向量，当然这里假定了v⁰包含此特征向量。

幂法的收敛速度取决于比值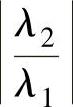。因此如果|λ₂|只比|λ₁|小一点，那么幂法会收敛得很慢，需要很多次的迭代才能得到符合精度要求的结果。

存在几种幂法的扩展方法。例如，如果需要求的是绝对值最小的特征值而不是主特征值，那么可以将幂法应用于A^-1。因为A^-1的特征值是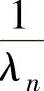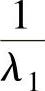，…，，反幂法的收敛结果将会是。

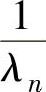另一种扩展方法是频谱移位。这个方法利用了A-aI的特征值是λ₁-a，…，λ_n-a这个性质。这样，在计算出了第一个特征值λ₁后，可以将幂法再次应用于移位矩阵A-λ₁I上。这将会使得第一个特征值减小到0，此时幂法将会向λ₂-λ₁，…，λ_n-λ₁中绝对值最大的那一个收敛。