最优功率分配方案求解：基于最小二乘法的负荷曲线拟合

1.一个三机电厂的燃料费用如下：

F₁：173.61+8.670P₁+0.00230P²₁ 美元/MWh

F₂：180.68+9.039P₂+0.00238P²₂ 美元/MWh

F₃：182.62+9.190P₃+0.00235P²₃ 美元/MWh该电厂的热负荷曲线如图6.8所示。计算并画出每台机组的最优出力和整个电厂的增量费用（λ）。

2.采用最小二乘法根据下面的测量数据求如下函数的最优系数c₀和c₁。

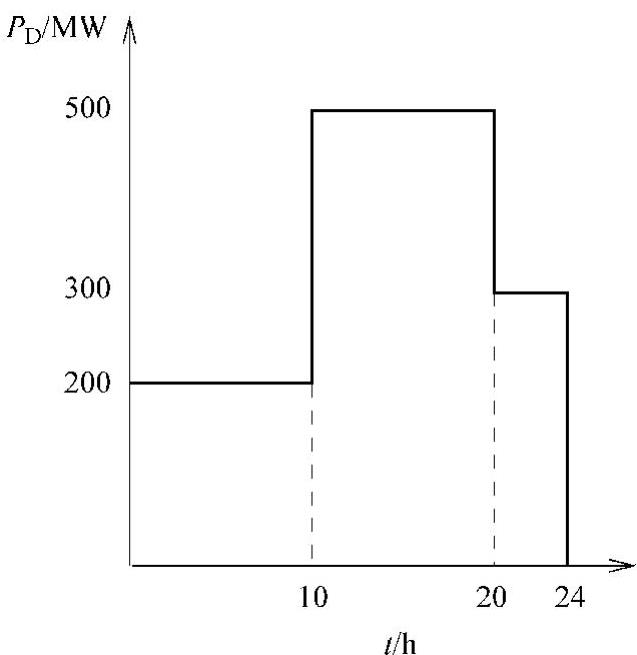
图6.8 问题1的负荷曲线

f（x）=c₀+c₁x

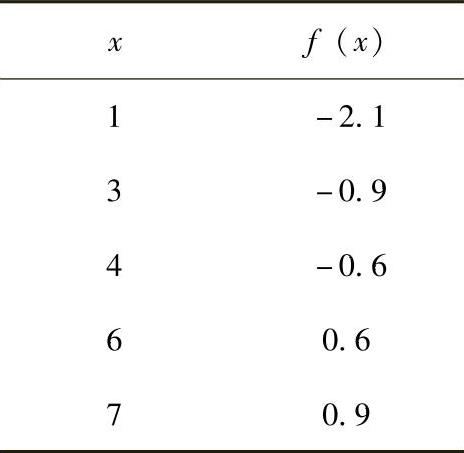
3.采用最小二乘法根据下面的测量数据求如下函数的最优系数a₀、a₁和a₂。此函数描述了潮汐在12h间隔内的运动。

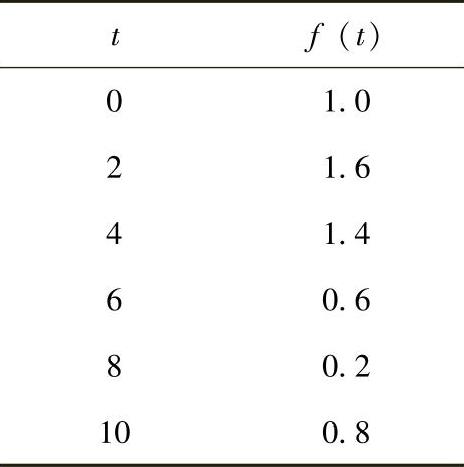
4.最小化-7x₁-3x₂+x₃，约束条件为

x₁+x₂+x₃≤15

2x₁-3x₂+x₃≤10

x₁-5x₂-x₃≤0

x₁，x₂，x₃≥0

（a）使用单纯形法。

（b）使用原始仿射方法，取α=0.9。

两种方法都用松弛变量x₄，x₅，x₆进行增广，并采用初始可行解向量x⁰=

[1 1 1 12 10 5]^T启动。

5.采用最速下降法，最小化x²₁+x²₂，约束条件为

x²₁+2x₁x₂+3x₂²-1=0

6.求目标函数C：x²₁+x²₂+u₁x₁+u₂x₂+1最小值。约束条件为

（a）x₁cos（x₂）+x²₂-u₁cos（x₁）=1

x₁-x₂+3u₂=-3(www.xing528.com)

（b）x₁cos（x₂）+x²₂-u₁cos（x₁）=1

x₁-x₂+3u₂=-3

u₂≥-0.8

（c）x₁cos（x₂）+x²₂-u₁cos（x₁）=1

x₁-x₂+3u₂=-3

x₂≤0.30

使用惩罚函数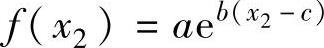，其中a和b是正的常数，c是函数的偏移量。

初始值为x⁰=[0 0]′，u⁰=[0 0]′，取γ=0.05。也可以取其他的γ值进行试验。停止计算的准则是‖C‖≤0.01。

7.用SQP方法重新做问题6。

8.考虑如图6.9所示的系统，母线和线路数据如下：

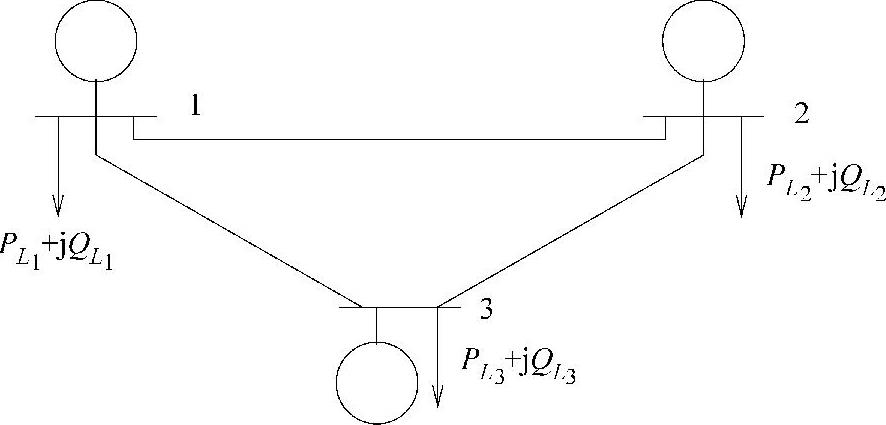
图6.9 三母线系统

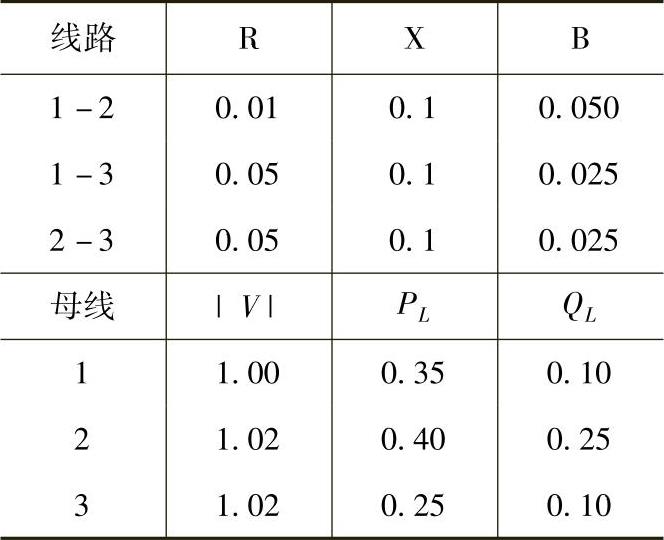
发电机的燃料费用如下：

（a）采用等增量费用准则，求发电机组的最优功率分配方案，记住这种方法是忽略系统损耗的。

（b）采用（a）的解作为初始控制向量，并采用最速下降法求解考虑系统损耗后的发电机组的最优功率分配方案。

（c）现在假定发电机出力具有如下的约束条件，重新做一遍（b）：

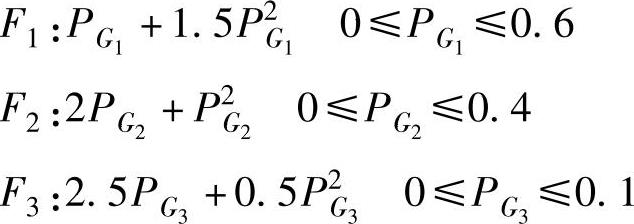
（d）将发电机出力与费用函数联系起来，解释你的结果。

9.对于如图6.9所示的系统，具有如下的量测数据：

其中σ²_V=（0.01）²，，。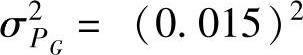

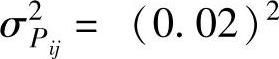根据系统的状态，求误差，并用显著性水平α=0.01的χ²检验检测是否存在坏数据。