电力系统状态估计器的设计与优化

在电力系统状态估计中，估计的变量是系统中的母线电压模值和母线电压相角。状态估计器的输入是实测的有功功率和无功功率，可以是注入母线的有功功率和无功功率，也可以是输电线路上的有功功率和无功功率。状态估计器的设计目标是得到母线电压模值和相角的最优估计值，使测量误差的影响最小化。状态估计器需要考虑的另一个因素是量测量是否足够用来完整地估计出系统的状态，即系统的可观察性问题。

如果由电力系统所有母线电压模值和相角构成的状态向量可以通过一组特定的量测量估计出来，那么这组特定的量测量被称为是可观察的。一个不可观察的系统意味着量测量的集合不能张满整个状态空间。如果式（6.47）中矩阵H_x的秩是n（满秩的），那么此电力系统是可观察的，这里量测量的个数m大于或等于系统状态量的个数n。所谓的冗余量测量指的是增加这些量测量后并不提高矩阵H_x的秩。

电力系统的可观察性可以通过检查量测量集合和电力系统结构来确定。树是一个可以覆盖整个电力系统母线的量测量集合（节点或支路）。换句话说，通过在图上连接母线和支路，系统的所有母线被连接在一个连通图中。通过在能连接分离的树的支路上增加量测量，可以将电力系统变为可观察的。

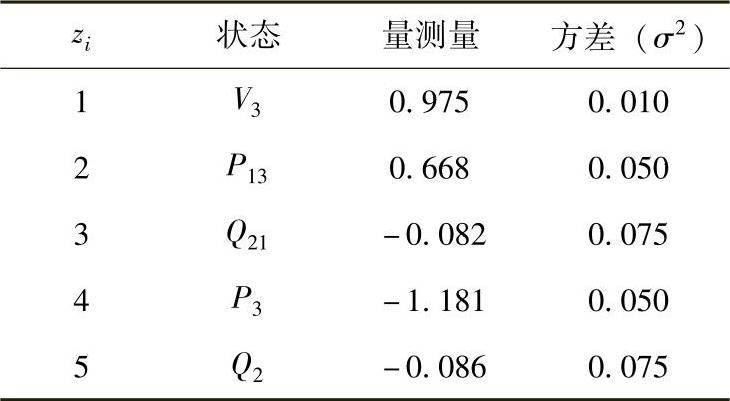
例6.17 图6.7所示电力网络的SCADA系统具有如下的量测量和方差，试估计系统的状态，并用显著性水平为α=0.01的χ²检验检测量测量中是否存在坏数据。

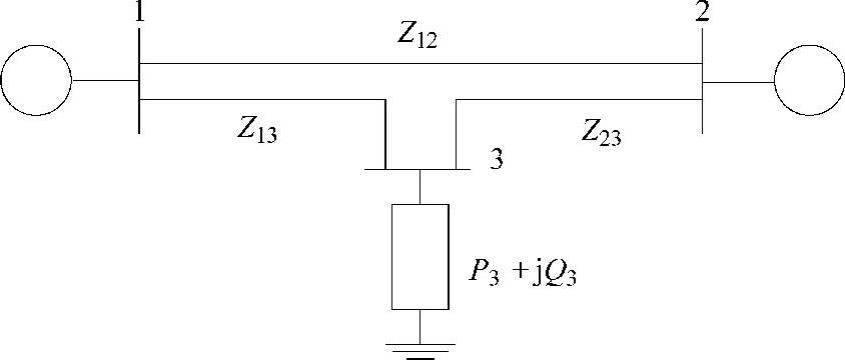
图6.7 电力系统图

解6.17 状态估计过程的第一步是确定并列举未知状态量。在本例中，未知状态量是[x₁x₂x₃]^T=[δ₂δ₃V₃]^T。确定状态量以后，下一步就是确定与每个量测量对应的函数h（x）。为了使加权误差最小化，需要将如下的非线性函数驱动到零：

F（x）=H_x^TR^-1[z-h（x）]=0 （6.155）

式中，z-h（x）的集合是

z₁-h₁（x）=V₃-x₃

z₂-h₂（x）=P₁₃-（V₁x₃Y₁₃cos（-x₂-ϕ₁₃）-V²₁Y₁₃cosϕ₁₃）

z₃-h₃（x）=Q₂₁-（V₂V₁Y₂₁sin（x₁-ϕ₂₁）+V²₂Y₂₁sinϕ₂₁）

z₄-h₄（x）=P₃-（x₃V₁Y₃₁cos（x₂-ϕ₃₁）+x₃V₂Y₃₂cos（x₂-x₁-ϕ₃₂）

+x²₃Y₃₃cosϕ₃₃）

z₅-h₅（x）=Q₂-（V₂V₁Y₂₁sin（x₁-ϕ₂₁）-V²₂Y₂₂sinϕ₂₂

+V₂x₃Y₂₃sin（x₁-x₂-ϕ₂₃））

与式（6.155）对应的偏导数矩阵H_x为

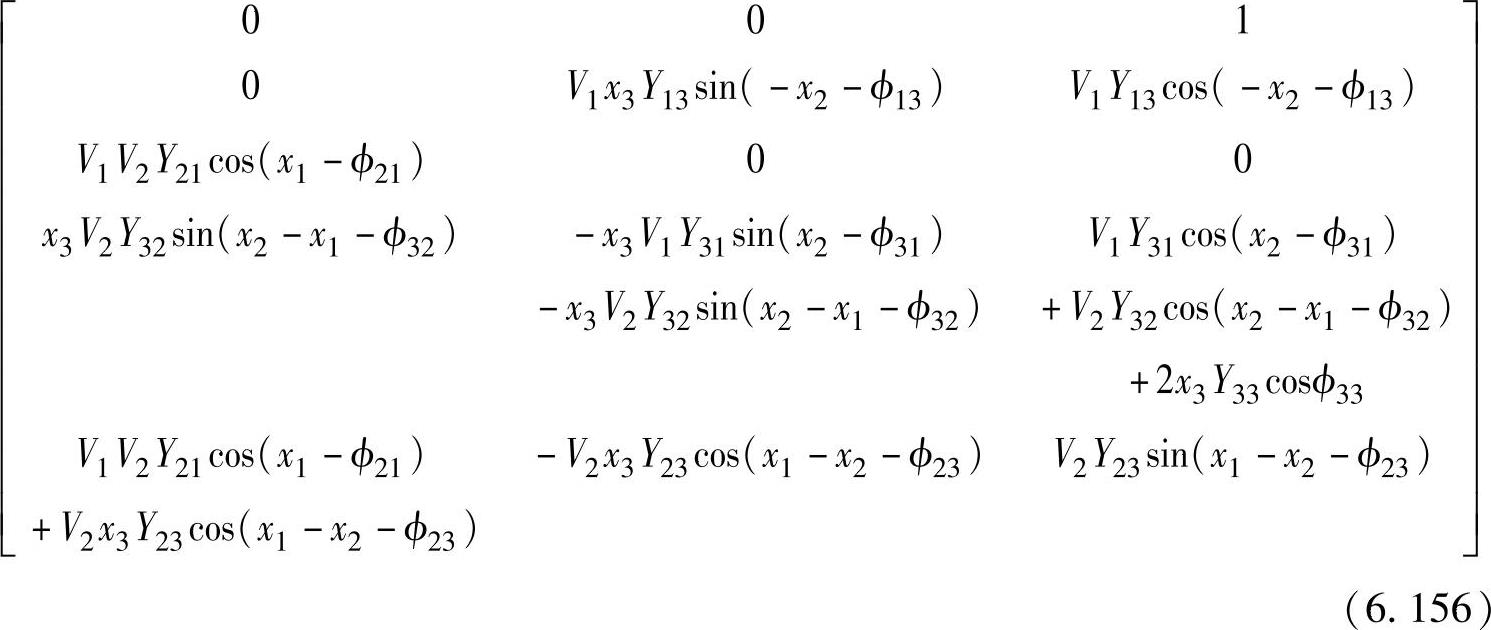
这个矩阵的秩为3，因此这组量测量张满了此电力系统的状态空间。

量测量的协方差矩阵为

使加权误差最小化的求解状态x的Newton-Raphson迭代式为

[H_x^T（x^k）R^-1H_x（x^k）][x^k-1_-xk]=H_x^T（x^k）R^-1[z_-h（x^k）] （6.158）

迭代1：

求解状态估计问题的初始条件与求解潮流方程相同，即平启动方式，也就是设置电压的模值为1，相角为0。在初始条件下测量函数h（x）的值为

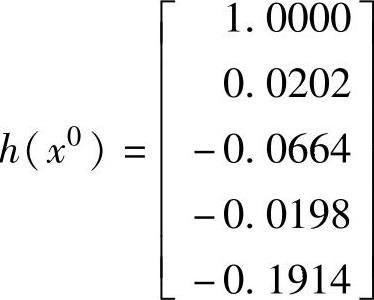
在初始条件下偏导数矩阵H_x的值为(https://www.xing528.com)

式（6.155）的非线性函数为

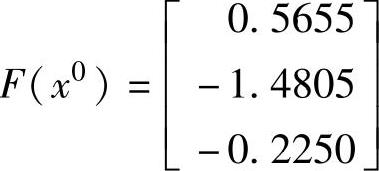
状态量的增量更新值为

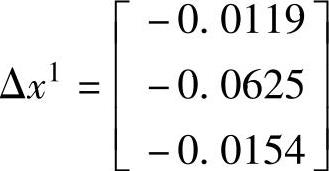
状态量的更新值为

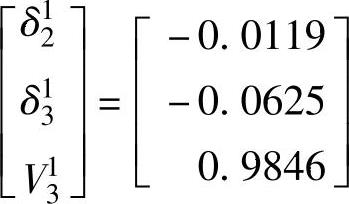
式中，δ₂和δ₃的单位是rad。首次迭代的误差为

ε⁰=1.4805

迭代2：

使用更新后的值重新计算Newton-Raphson迭代：

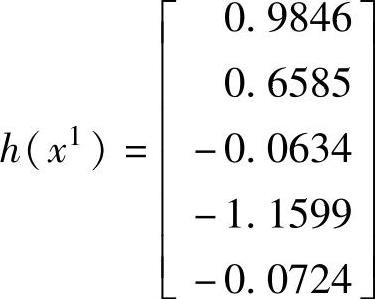
偏导数矩阵H_x为

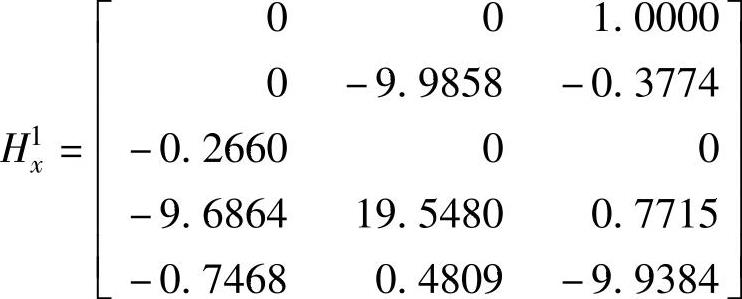
采用更新后的值计算非线性函数得

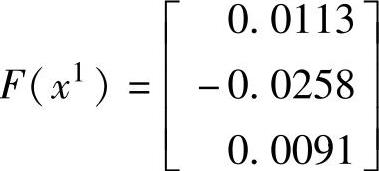
状态量的更新值为

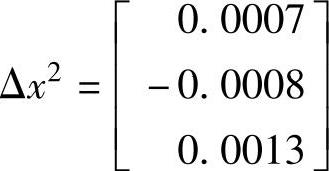
得第2次迭代的状态量为

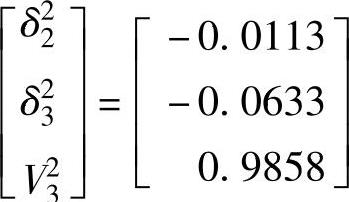
第2次迭代的误差为

ε¹=0.0258

此次迭代显然已收敛。收敛后使加权测量误差最小化的状态量为

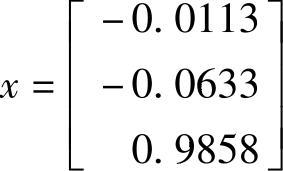
为了检查是否存在坏数据，将测量误差平方的加权和与自由度k=2和显著性水平α=0.01的χ²分布进行对比。测量误差平方的加权和为

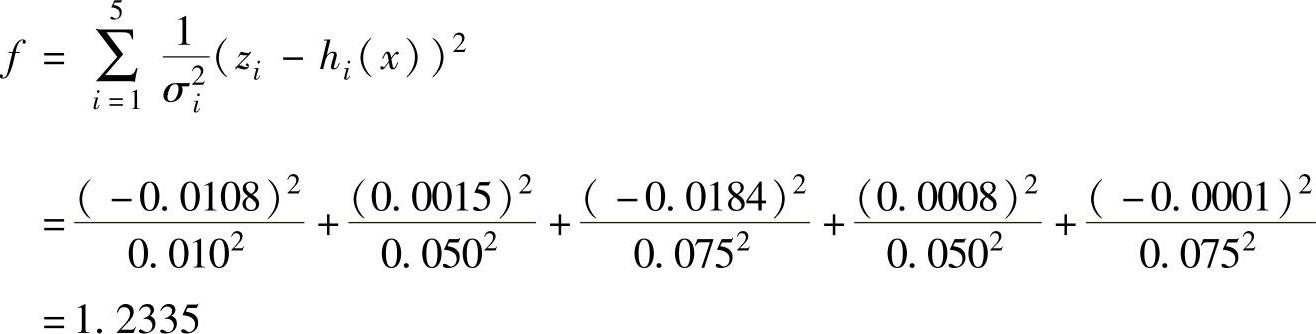
此值小于χ₂，0.01=9.21，故有理由相信数据良好，不存在任何虚假的量测量。