最优潮流问题及其在电力系统中的应用

在诸如潮流计算的很多电力系统应用中，只能给出电力系统运行的一个时间断面上的信息。而系统规划人员和运行人员经常更关注系统参数调整对流过线路的潮流以及对系统损耗的影响。对系统参数的调整不是随意的，通常根据某个目标函数对系统参数进行最优调整。这些目标函数可以是发电费用最小，水库水位最小，或者系统损耗最小，等等。最优潮流问题就是在目标函数的框架下建立潮流计算问题以求解系统电压和发电功率。在此应用中，潮流计算的输入参数会被系统性地进行调整，以最大化或最小化某个由潮流状态变量表示的标量函数。最常见的两个目标函数是最小化发电费用和最小化有功损耗。

最优潮流的时间尺度为分钟级到1h，因此其基本假设是只针对当前在线的机组进行优化。确定机组是否应该投入、何时投入、投入多长时间的机组组合问题，不在这里进行考虑。使输电系统有功损耗最小化，不但可以节省发电费用，还能增加系统的备用容量。

通常发电费用曲线（发电机发出的功率与发电费用之间的关系曲线）是由一段一段线性的增量费用曲线表示的。这是为了简化凹的费用函数所得到的结果，分段线性的增量费用曲线的断点与凹曲线的阀点重合^[19]。通过对增量费用曲线进行积分，可以将分段线性的增量费用曲线变为分段二次费用曲线。这种类型的目标函数使其很容易用于经济调度问题，即在优化过程中只考虑发电单元的λ-调度问题。在这种优化过程中，系统损耗以及电压约束和线路潮流约束都被忽略。这个经济调度方法将在下面的例子中具体说明。

例6.10 三台发电机具有如下的费用函数，供电给952MW的负荷，假定系统无损耗，计算最优的发电分配方案。

C₁：P₁+0.0625P²₁ 美元/h

C₂：P₂+0.0125P²₂ 美元/h

C₃：P₃+0.0250P²₃ 美元/h

解6.10 确定最优发电分配方案的第一步是将此问题构造成一般性的形式。因此，本问题的数学描述为

最小化C：P₁+0.0625P²₁+P₂+0.0125P²₂+P₃+0.0250P²₃

约束条件：P₁+P₂+P₃-952=0

根据上述数学描述，受约束的费用函数变为

C∗：P₁+0.0625P²₁+P₂+0.0125P²₂+P₃+0.0250P²₃-λ（P₁+P₂+P₃-952） （6.116）

令C^∗的导数为零，得到如下线性方程组：

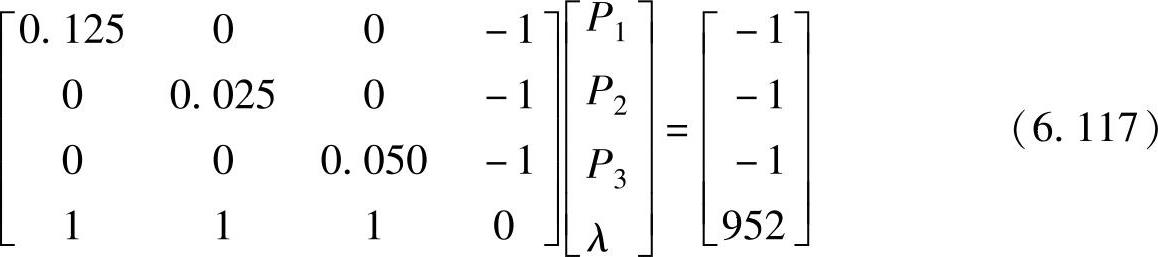
求解上述方程组得到

P₁=112MW

P₂=560MW

P₃=280MW

λ=15美元/MWh受约束的费用为7616美元/h。

这是一个使每小时发电费用最小化的发电分配方案。λ的值是发电费用的增量费用，即等价费用，也是公司买电或卖电的截止价格：如果公司能以低于λ的价格买电，那么公司的总费用将下降。同样地，如果公司能以高于λ的价格卖电，公司的总费用也将下降。同时请注意在最优分配方案下：

λ=1+0.125P₁=1+0.025P₂=1+0.050P₃ （6.118）

因为λ是系统的增量费用，该点也被称作“等增量费用点”，而该发电分配方案被说成是满足“等微增量费用准则”。任何偏离等微增量费用准则的发电分配方案都会导致发电费用C的上升。

例6.11 若用户愿意支付16美元/MWh买电，有多少超额电量可以生产和销售？此交易的利润是多少？

解6.11 从例6.10知道，通过对增广费用函数求导，可以得到发电量与λ之间的关系为

P₁=8（λ-1）

P₂=40（λ-1）

P₃=20（λ-1）

因此根据等式约束条件有

8（λ-1）+40（λ-1）+20（λ-1）-952=0 （6.119）

为了确定超额电量，需对式（6.119）进行增广，并计算λ=16美元/MWh时的值：

8（16-1）+40（16-1）+20（16-1）-（952+超额量）=0 （6.120）

求解式（6.120）得超额电量为68MW，且P₁=120MW，P₂=600MW，P₃=300MW。发电总费用变为

C：P₁+0.0625P²₁+P₂+0.0125P²₂+P₃+0.0250P²₃=8670美元/h （6.121）

卖出超额电量所得到的收入等于超额电量乘增量费用λ，

68MW×16美元/MWh=1088美元/h

因此，总的费用为8670美元/h-1088美元/h=7582美元/h。比上例中的费用7616美元/h减少36美元/h，因此这36美元/h是通过以16美元/MWh价格卖出超额电量所获得的利润。

图6.5展示了一个中等规模电力公司的发电增量费用表。发电机的增量费用从上到下列在表格的左边；不同发电机单元列在表格的顶部，由最便宜的左边到最贵的右边依次排列。核电机组运行费用最低，最左端的核电机组Washington能够以7美元/MWh的增量费用提供至多1222MW的功率；它的增量费用只有第二便宜的燃煤机组Adams（14美元/MWh）的一半。随着启用的机组变得越来越贵，增量费用也相应提高。

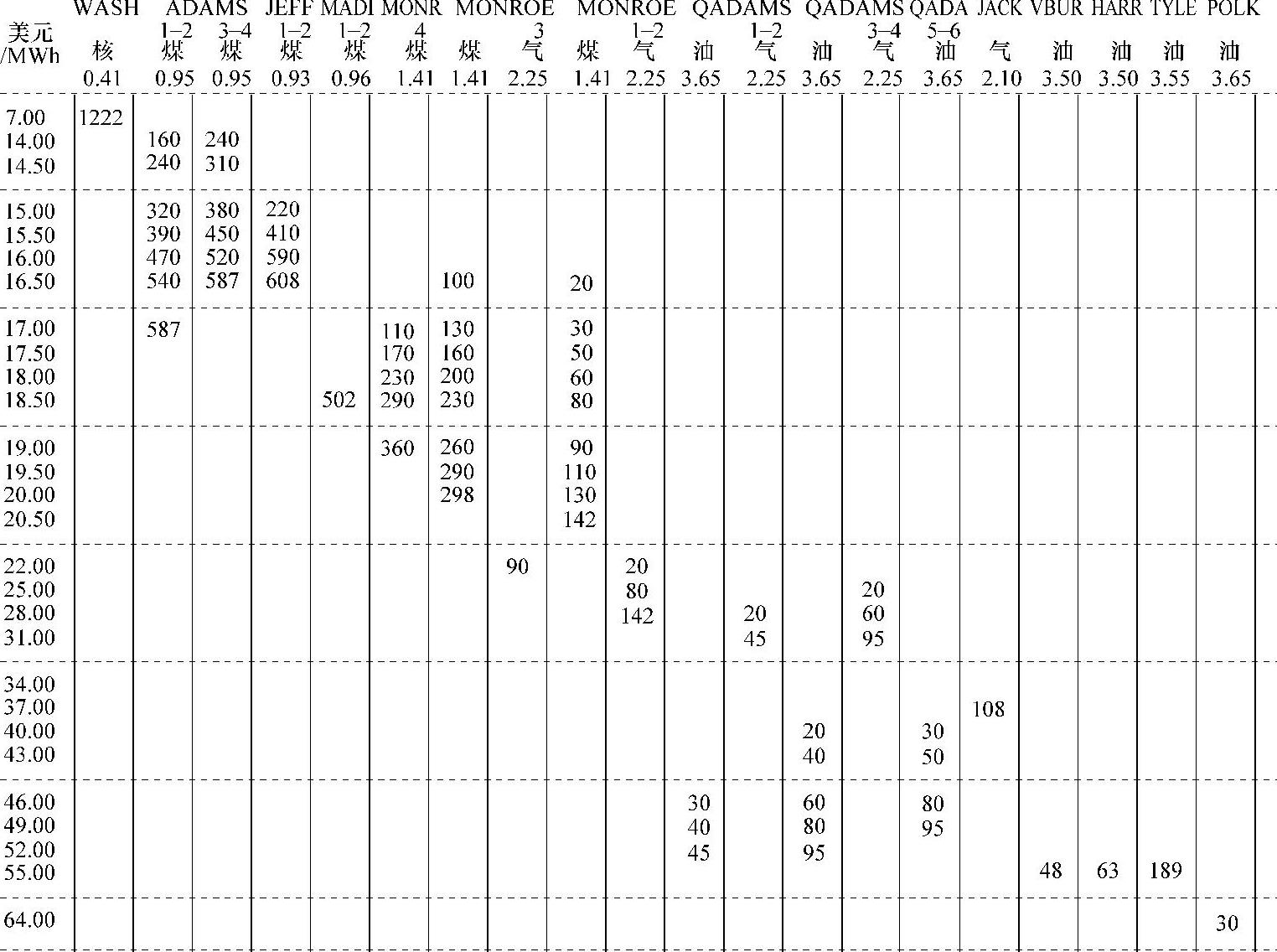
图6.5 增量费用表

例6.12 生产4500MW电力，上述电力公司的增量费用是多少？

解6.12 为了从图6.5的增量费用表中找到对应4500MW时的增量费用，需要对各台发电机的最大出力进行累加直到等于4500MW。经过计算可知，当累加到燃气机组Monroe1-2时可以达到4500MW的出力，而所对应的增量费用是28美元/MWh。这是发电4500MW时的平衡点价格。

如果购电价格可以低于28美元/MWh，该电力公司就应该买电。

等增量费用发电分配方案的主要缺陷是忽略了系统的损耗。其唯一的约束是一个等式约束，即发电总量必须等于负荷总量。但实际上，发电总量总是等于负荷总量加系统损耗。考虑损耗后，等式约束必须包括潮流方程，而优化过程必须采用最速下降法或类似的方法等^[10]。

例6.13 考察如图6.6所示的三机系统。该系统与例3.9的三机系统具有相同的参数，除了母线3已转化为发电机母线且其电压模值等于1.0pu。总负荷和发电机的费用函数与例6.10相同。采用等增量费用准则作为起始点，求解考虑损耗后此系统的最优发电分配方案。

解6.13 采用6.3.2节描述的最速下降法，第一步是求梯度C的表达式，本例中，

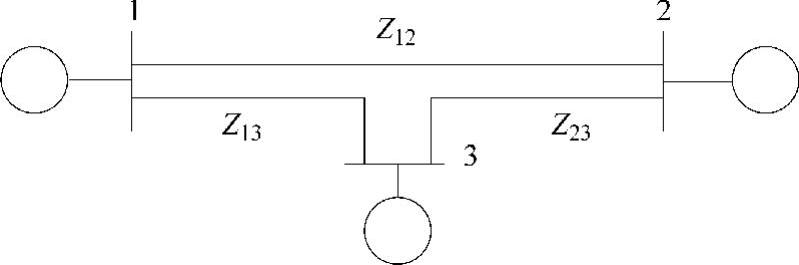
图6.6 例6.13的系统图

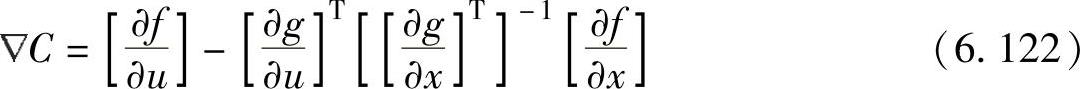
式中，f是发电机费用之和

f：C₁+C₂+C₃=P₁+0.0625P²₁+P₂+0.0125P²₂+P₃+0.0250P²₃

g是潮流方程组：

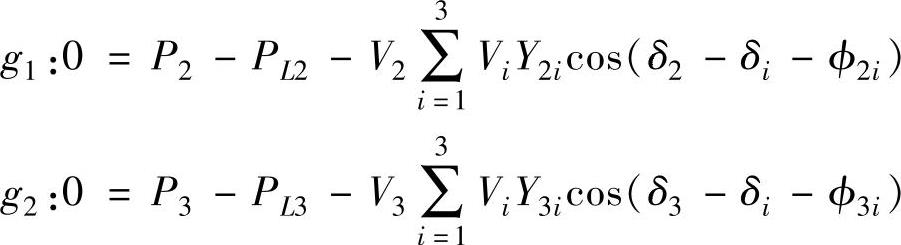
式中，P_Li表示母线i的有功负荷，输入变量u是独立的发电机出力：

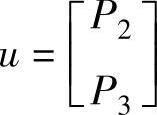
而x是未知的状态变量

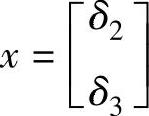
发电机出力P₁不是输入变量，因为母线1是平衡母线，其发电出力不是独立变量。根据上述描述，可以导出用于C计算的各个偏导数为

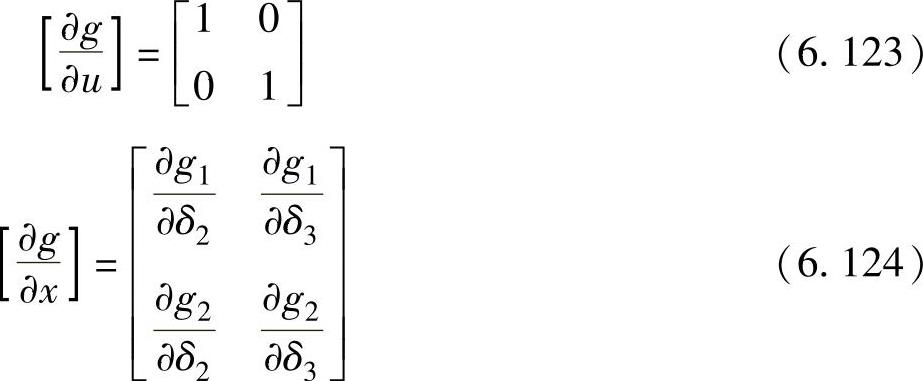
式中，

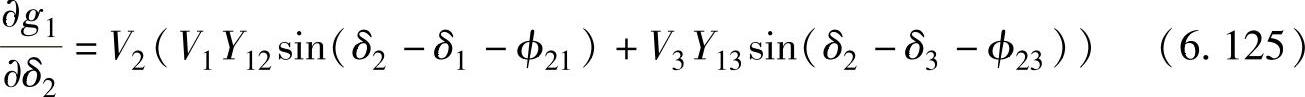
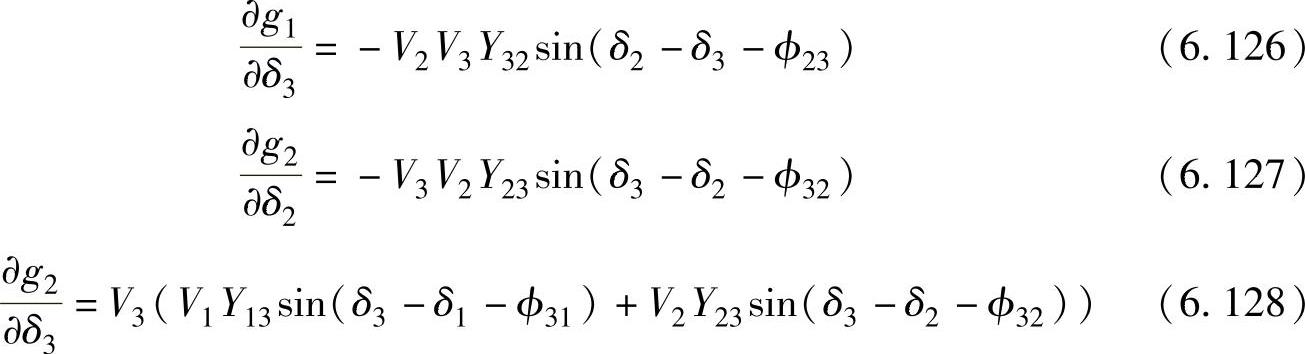
且(www.xing528.com)

求偏导数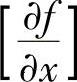较为复杂，因为费用函数并没有直接写成x的函数。但是，回想一下，P₁不是输入变量，实际上是一个依赖于x的变量，即

P₁=V₁（V₁Y₁₁cos（δ₁-δ₁-ϕ₁₁）

+V₂Y₁₂cos（δ₁-δ₂-ϕ₁₂）+V₃Y₁₃cos（δ₁-δ₃-ϕ₁₃）） （6.130）

因此，根据链式法则，

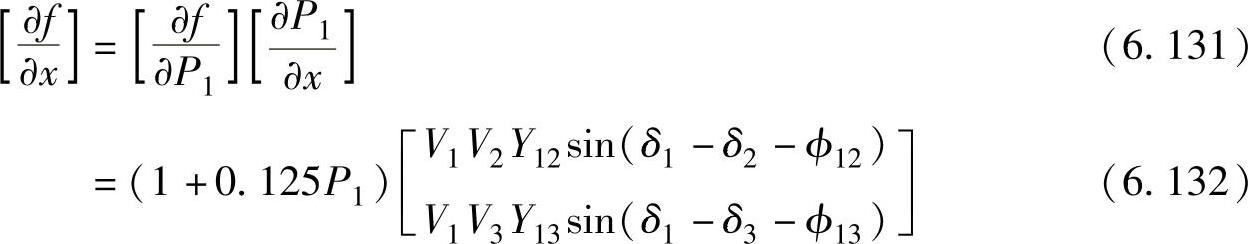
根据前面的算例，由等增量费用准则得到的初始值为P₂=0.56pu和P₃=0.28pu。采用P₂=0.56pu和P₃=0.28pu作为输入求解潮流方程，得到如下状态量：[δ₂δ₃]=[0.0286 -0.0185]，P₁=0.1152。将发电出力转换为MW，再将其数值代入到偏导数中得到

从而得到

这样，输入量（发电出力）的新值为

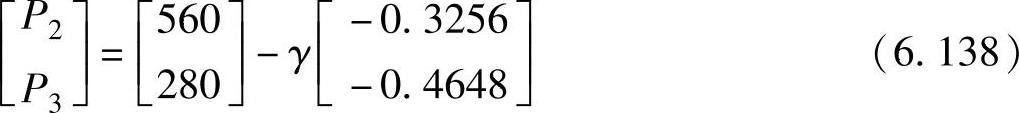
取γ=1时，更新后的发电出力为P₂=560.3MW和P₃=280.5MW。

这里梯度C已经很小了，表示根据等增量费用准则得到的发电出力即使在考虑了损耗后也已相当接近于最优值。再经过一次迭代，得到三台发电机最终出力值为

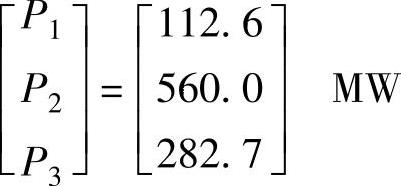
此条件下的发电费用为7664美元/MWh。注意，这个发电费用高于用等增量费用准则计算得到的发电费用，其原因是需要增加额外发电出力以补偿系统的损耗。

最速下降法有时会使系统状态或输入超出物理约束，例如使用该算法会导致发电出力超出机组的最大物理出力。类似地，所得到的母线电压也可能超出期望的变化范围（通常为额定值的±10%范围）。这些情况都属于违反了此问题的不等式约束。在这些情况下，必须对最速下降法进行修正以反映这些物理约束。已存在数种方法来考虑上述约束，可以将这些方法分为取决于输入的约束（独立变量）和取决于状态的约束（非独立变量）。

6.4.1.1 对独立变量的约束

如果应用最速下降法得到输入变量的更新值超出了设定的极限，那么最直接的解决方法是将越限的输入变量值设置成等于其极限值，然后继续往下计算，只是减少了一个自由度。

例6.14 重复例6.13，但发电机必须满足如下限制条件：

80MW≤P₁≤1200MW

450MW≤P₂≤750MW

150MW≤P₃≤250MW

解6.14 根据例6.13的结果，发电机3的输出超出了其极限值0.25pu。因此在例6.13的第1次迭代以后，P₃被设置为0.25pu，则新的偏导数为

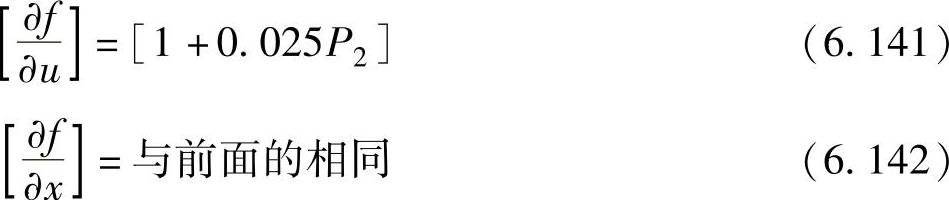
根据带约束的最速下降法，新的发电机出力为

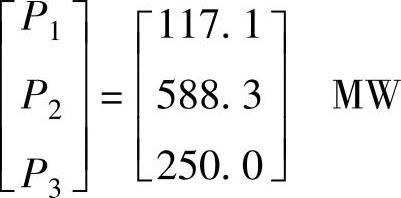
此时发电费用为7703美元/MWh，高于无约束的发电费用7664美元/MWh。随着更多的约束被加入进来，系统会离最优工作点越来越远，从而增加了发电费用。

6.4.1.2 对非独立变量的约束

在很多情况下，系统的物理约束是施加在状态变量上的，而状态变量在系统描述中是因变量。这种情况下，不等式约束是状态变量x的函数，并且必须加入到费用函数中去。对因变量有约束的例子包括最大线路潮流和母线电压水平。在这些情况下，状态变量的值是不能独立设定的，而必须间接确定。执行不等式约束的一种方法是在费用函数中引入惩罚函数。惩罚函数是这样一种函数，当状态变量离极限值很远时很小，但当状态变量接近极限值时会变得很大。典型的惩罚函数包括：

p（h）=e^khk>0 （6.143）

p（h）=x²ⁿe^khn，k>0 （6.144）

p（h）=ax²ⁿe^kh+be^khn，k，a，b>0 （6.145）

而费用函数变为

C^∗：C（u，x）+λ^Tg（u，x）+p（h（u，x）-h^max） （6.146）

上述费用函数可以通过一般的导数为零的方法得到其最小值。这种方法的优势是实现简单，但也存在几个缺陷。第1个缺陷是惩罚函数的选择经常是启发式的，随不同的问题而不同。第2个缺陷是此种方法不能实施对状态变量的硬约束，即如果超出极限值，费用函数会变得很大，但状态变量是允许超出极限值的。在很多应用中，上述问题不算很严重的缺陷。如果输电线路上的潮流略微超出其极限，可以认为电力系统仍然能够继续运行，至少在一个有限的时间段内。然而，若物理约束是一架飞机高于地面的高度，那么即使是很小的高度负偏差，也会造成可怕的后果。因此，使用惩罚函数来实施约束时一定要小心，并不是对所有系统都适用。

例6.15 重新计算例6.13，但需通过惩罚函数限制线路2-3的潮流至0.4pu。

解6.15 例6.13中流过线路2-3的潮流为

P₂₃=V₂V₃Y₂₃cos（δ₂-δ₃-ϕ₂₃）-V₂²Y₂₃cosϕ₂₃=0.467 （6.147）

若P₂₃超过0.4pu，则惩罚函数

p（h）=（1000V₂V₃Y₂₃cos（δ₂-δ₃-ϕ₂₃）-1000V²₂Y₂₃cosϕ₂₃-400）² （6.148）

将加到费用函数中去。除了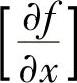，其余偏导数保持不变。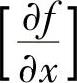的表达式为

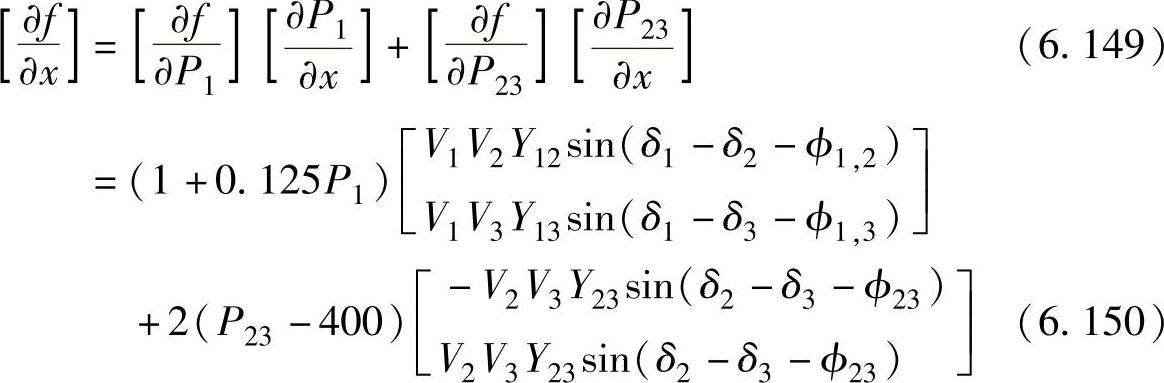
采用最速下降法进行计算，得到受约束下的最优发电方案为

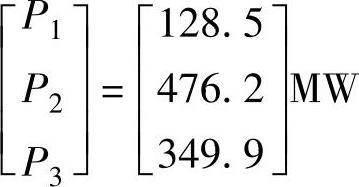
而P₂₃=400MW。该受约束最优发电方案下的发电费用为7882美元/MWh，略微高于无约束的最优方案。

对于必须施加硬约束的情况，须采用替代方法来执行不等式约束。在本方法中，不等式约束是作为额外的等式约束加入到费用函数中的，即把不等式约束转化为等于上限或下限的2个等式约束。这本质上是引入了额外的一组Lagrange乘子。因此本方法经常被称为对偶变量法，因为每个不等式约束都可能引出两个等式约束，一个对应上限约束，另一个对应下限约束。然而，不可能同时违反上限约束和下限约束，因此对于任何给定的工作点，在2个额外的Lagrange乘子中只要取其中一个就可以了，即对偶约束是相互排斥的。

例6.16 采用对偶变量法重新计算例6.15。

解6.16 通过引入额外的等式方程

P₂₃=V₂V₃Y₂₃cos（δ₂-δ₃-ϕ₂₃）-V₂²Y₂₃cosϕ2₃=0.400 （6.151）也就是在等式约束方程组g（x）中额外增加了一个方程，因此，在状态向量x中必须增加一个额外的未知量，以构造一个可以求解的方程组（三个方程三个未知数）。P_G2和P_G3中任何一个都可以被选作新的未知量。本例中，选择P_G3作为新的未知量。新系统Jacobi矩阵为

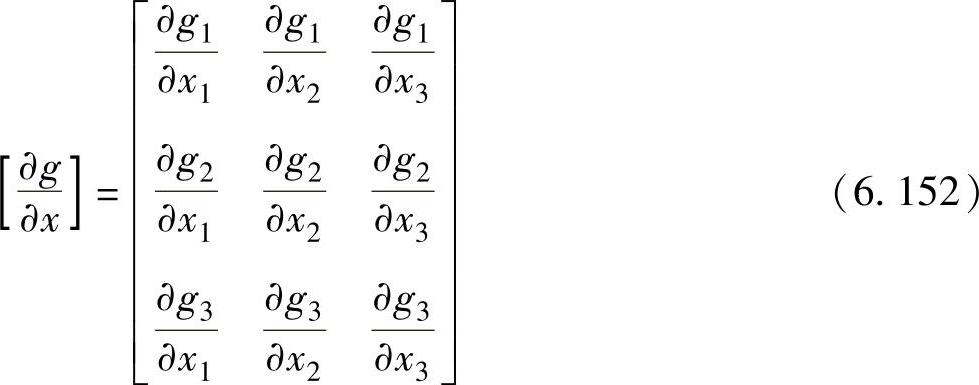
式中，

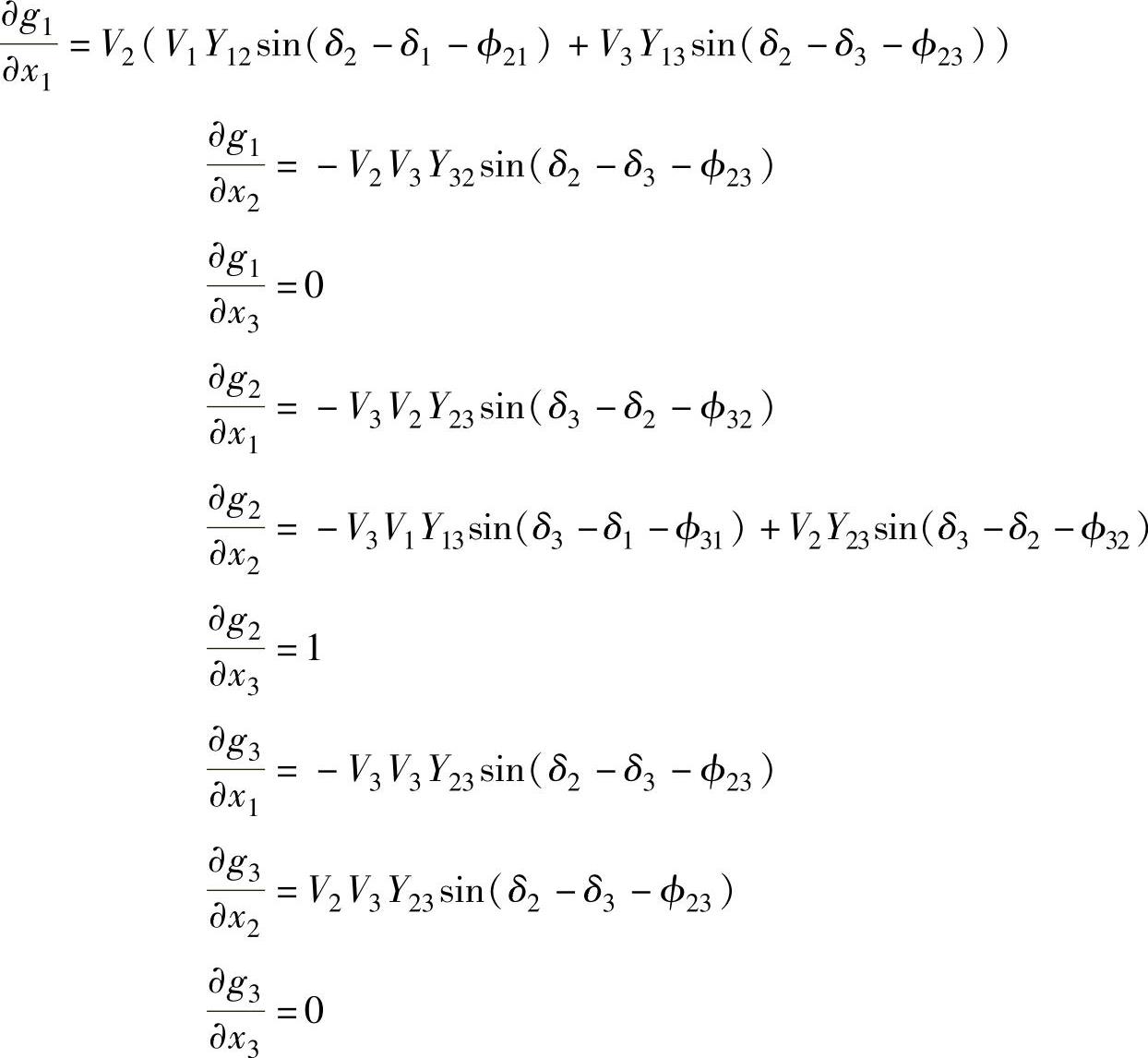
且

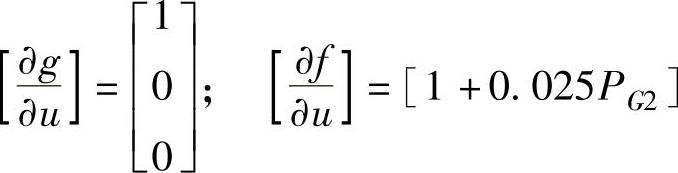
与例6.13类似，通过链式法则计算：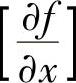

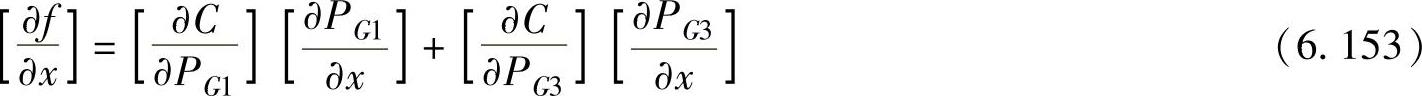
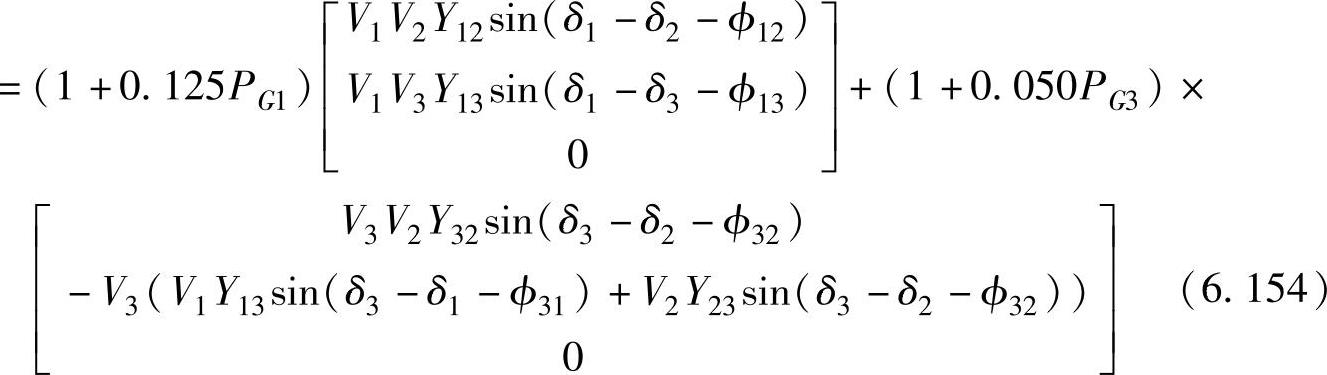
将这些偏导数代入到C的式（6.122）中，可以得到与例6.15相同的发电分配方案。