使用序贯二次规划法的优化方法

梯度下降法在小型非线性系统中很有效，但在搜索空间维数上升时效率降低。非线性序贯二次规划（SQP）法计算高效，且已证明在凸搜索空间中表现出超线性收敛特性^[4]。SQP方法用于求解如下问题：

最小化

f（x） x∈Rⁿ （6.105）

约束条件为

c_i（x）=0，i∈ξ （6.106）

h_i（x）≥0，i∈Ξ （6.107）

与前文类似，求解该优化问题的常规方法是利用Lagrange乘子，使如下混合系统最小化：

L（x，λ）-f（x）+λ^Tc（x）+π^Th（x） i=1，…，m （6.108）

KKT条件为

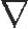f（x）+C^Tλ+H^Tπ=0

c（x）=0

h（x）+s=0

π^Ts=0

π，s≥0

式中，λ是等式约束的Lagrange乘子向量，π是不等式约束的Lagrange乘子向量，s是松弛变量向量，而

这组非线性方程可以通过Newton-Raphson法求得x、λ、π和s。考虑只有x和λ的情况，利用Newton-Raphson法求解y=[xλ]^T，有

Newton-Raphson法的向量y更新为

y^k+1=y^k-α_k[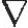F_k]^-1F（y^k）

用原变量表达为(www.xing528.com)

式中，α_k是步长，大于零，通常取小于或等于1的值。

例6.9 用SQP法重新做例6.8。

解6.9 将问题重新写出如下：

最小化

C：x²₁+2x²₂+u²=f（x₁，x₂，u） （6.112）

约束条件为

0=x²₁-3x₂+u-3 （6.113）

0=x₁+x₂-4u+2 （6.114）

运用KKT条件，得到如下的非线性方程组：

0=2x₁+2λ₁x₁+λ₂

0=4x₂-3λ₁+λ₂

0=2u+λ₁-4λ₂

0=x²₁-3x₂+u-3

0=x₁+x₂-4u+2

Newton-Raphson迭代式为

从初始解[x₁x₂uλ₁λ₂]^T=[1 1 1 1 1]^T开始，得到后续的更新解为

这与前面已得到的结果是一致的。