优化工程应用中的非线性规划问题：最速下降法

在工程应用中，一般性的非线性规划问题通常采用两类方法进行求解：

1.梯度法，如最速下降法。

2.迭代法，如逐次二次规划法。

在无约束系统中，通常求解函数f（x）最小化问题的方法是令函数的导数为零，然后根据导数方程求解出系统的状态。然而，对于大多数应用，在无约束最小化条件下得到的系统状态将不能满足约束方程。因此，需要寻找一种替代的方法来求解带约束的最小化问题。其中的一种方法是引入附加的参数集λ，通常被称为Lagrange乘子，将约束条件加入到费用函数中。这样，增广后的费用函数变为

最小化 f（x）-λc（x） （6.91）

式（6.91）的增广函数最小化问题，可以通过令增广函数的导数为零进行求解。注意，式（6.91）关于λ的导数，所得到的就是式（6.64）的等式约束。

例6.7 最小化

约束条件为

2x-y=5

解6.7 注意，要使其最小化的函数是一个圆的方程。此函数的无约束最小值在原点x=0和y=0上取到，意味着此圆的半径为零。然而，加上约束条件后，此圆必须与给定的直线相交，因此，此圆的半径不能为零。增广的费用函数变为

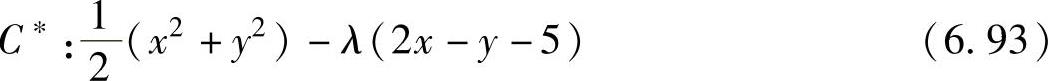
式中，λ表示Lagrange乘子。令增广费用函数的导数为零，得到如下方程组：

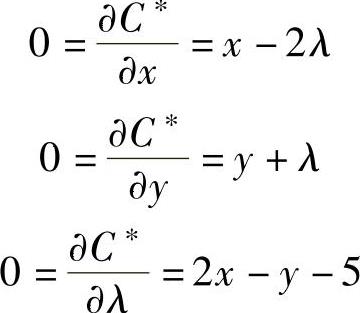
求解此方程组得到[xyλ]^T=[2 -1 1]^T。在增广费用函数取到最小值的点上，费用函数式（6.92）的值为

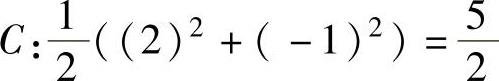
费用函数f和约束方程c也可能是某个外部输入u的函数，在最小化函数f（x）的过程中，u是可变的。在这种情况下，式（6.91）可以更一般地表示为

最小化f（x，u）-λc（x，u） （6.94）

如果等式约束超过一个，那么λ就变为一个乘子向量，增广费用函数变为

C^∗：f（x）-[λ]^Tc（x） （6.95）式中，C∗的导数变为

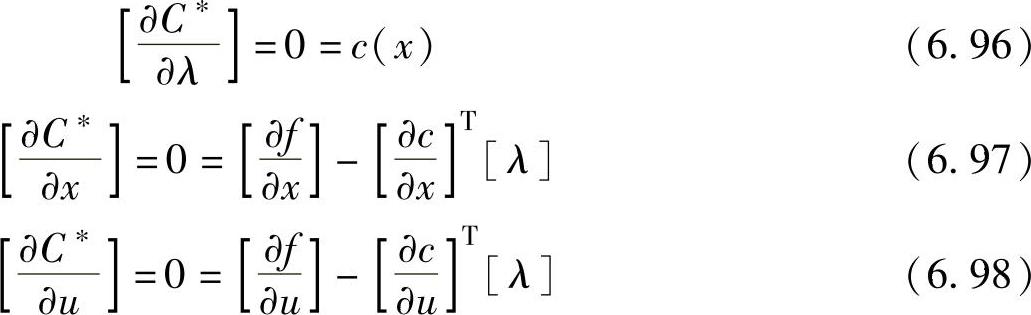
注意，对任何满足等式约束的可行解，都满足式（6.96）；但可行解不一定是使费用函数最小化的最优解。在这种情况下，[λ]可以从式（6.97）中得到，

且只有

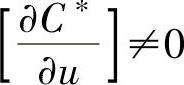
这个向量可以被用作梯度向量[C]，它和费用函数C的等值线正交。这样

而

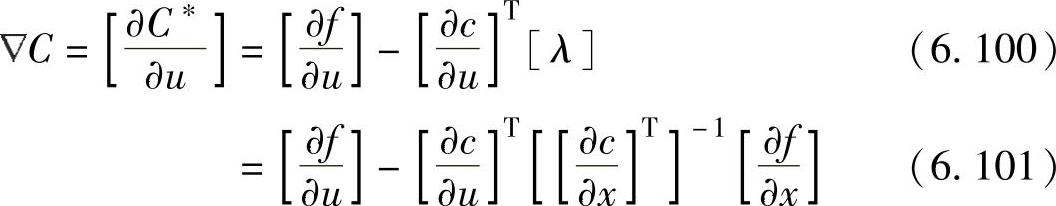
上述方法给出了此优化算法的基础，此优化算法被称为最速下降法。

最速下降法的步骤

1.令k=0。给定一个初始向量u^k=u⁰。

2.求解式（6.96）（可能是非线性的），得到可行解x。

3.根据式（6.101）计算C^k+1和C^k+1。若‖C^k+1-C^k‖小于事先设定的误差，则停止。

4.计算新的向量u^k+1=u^k-γC，其中γ是用户设定的大于零的算法步长。

5.k=k+1。返回步骤2。

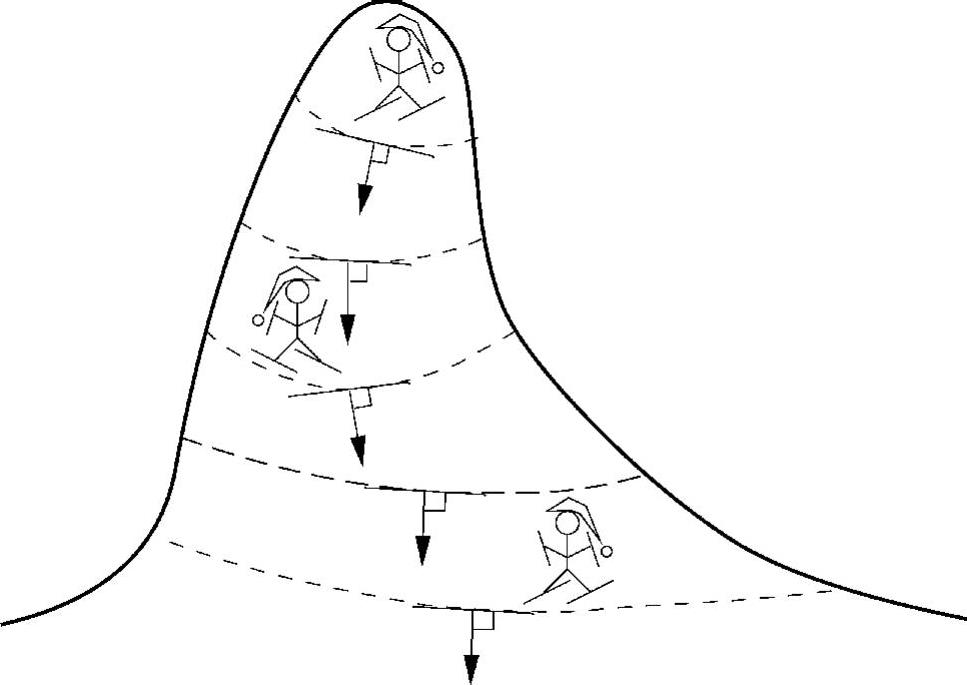
图6.4 最速下降法的例子

在最速下降法中，每一步都要确定向量u的移动方向，该方向就是增广费用函数C^∗变化最快的方向。例如，考虑一个人从山顶滑雪至山脚，如图6.4所示。滑雪者会在某一段路径上直线前进。在此点上，他也许并不是直指山下滑行的。因此。他会不断调整，以使自己朝着最速下降的方向前进。最速下降的方向与等高线（即费用）的切线垂直。滑雪者每次调整方向间的移动距离与算法中的步长γ是类似的。当γ较小时，滑雪者会频繁地改变方向，这样，他的下降速度不高。而当γ较大时，他可能会越过山脚重新上坡。因此，最速下降法的关键在于γ的选择。如果γ选得小，算法更容易收敛到最小值，但需要更多的迭代次数。相反地，大的γ会导致在最小值附近振荡。

例6.8 最小化

C：x²₁+2x²₂+u²=f（x₁，x₂，u） （6.102）

约束条件为(www.xing528.com)

0=x²₁-3x₂+u-3 （6.103）

0=x₁+x₂-4u+2 （6.104）

解6.8 为了求解式（6.101）的C，需要如下的偏导数：

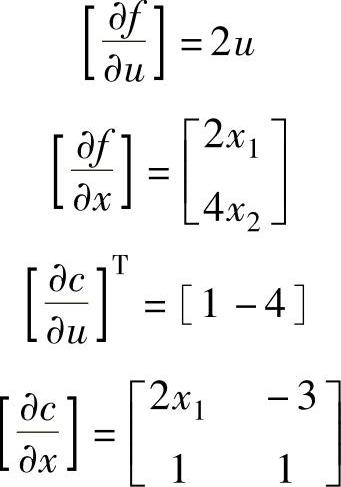
可以得到

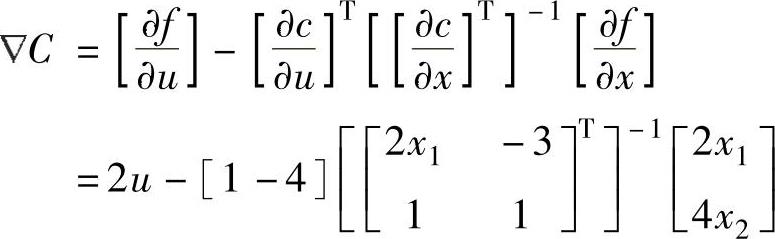
迭代1

令u=1，γ=0.05，选择停止迭代的准则为∈=0.0001。求解x₁和x₂，得到两组解及其对应的费用函数：

x₁=1.7016 x₂=0.2984 f=4.0734

x₁=-4.7016 x₂=6.7016 f=23.2828

第1组解得到了费用函数的极小值，因此被选择为工作解。将x₁=1.7016，x₂=0.2984代入到梯度函数中，得到C=10.5705，u的新值变为

u^（2）=u^（1）-γC

=1-（0.05）（10.5705）

=0.4715

迭代2

取u=0.4715，再次求解x₁和x₂，得到两组解及其对应的费用函数：

x₁=0.6062 x₂=-0.7203 f=1.6276

x₁=-3.6062 x₂=3.4921 f=14.2650

第1组解再次得到了费用函数的极小值，因此被选择为工作解。费用函数的差为

|C^（1）-C^（2）|=|4.0734-1.6276|=2.4458大于迭代停止准则。将这些值代入到梯度函数中，得到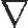C=0.1077，u的新值变为

u^（3）=u^（2）-γ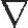C

=0.4715-（0.05）（0.1077）

=0.4661

迭代3

取u=0.4661，再次求解x₁和x₂，得到两组解及其对应的费用函数：

x₁=0.5921 x₂=-0.7278 f=1.6271

x₁=-3.5921 x₂=3.4565 f=14.1799

第1组解再次得到了费用函数的极小值，因此被选择为工作解。费用函数的差为

|C^（2）-C^（3）|=|1.6276-1.6271|=0.0005

大于迭代停止准则。将这些值代入到梯度函数中，得到C=0.0541，u的新值变为

u^（4）=u^（3）-γC

=0.4661-（0.05）（0.0541）

=0.4634

迭代4

取u=0.4634，再次求解x₁和x₂，得到两组解及其对应的费用函数：

x₁=0.5850 x₂=-0.7315 f=1.6270

x₁=-3.5850 x₂=3.4385 f=14.1370

第1组解再次得到了费用函数的极小值，因此被选择为工作解。费用函数的差为

|C^（3）-C^（4）|=|1.6271-1.6270|=0.0001

满足迭代停止准则。因此，问题的解为x₁=0.5850，x₂=-0.7315，u=0.4634，而费用函数的最小值为f=1.6270。