优化二次规划问题的求解方法及应用

非线性规划问题中的一个特殊子类是二次规划问题，其一般性表达式为最小化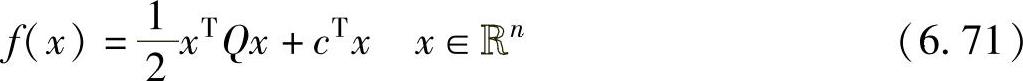约束条件为Ax≤b （6.72）

x≥0 （6.73）

如果Q是半正定矩阵，那么f（x）是凸函数。如果Q为零，那么此问题就变为线性规划问题。对此二次规划问题，Lagrange函数为

式中，λ是m维的行向量。对应局部最优点的KKT条件为

c^T+x^TQ+λA≥0 （6.75）

Ax-b≤0 （6.76）

x^T（c+Qx+A^Tλ）=0 （6.77）

λ（Ax-b）=0 （6.78）

x≥0 （6.79）

λ≥0 （6.80）

为了将这些方程改写为更易处理的形式，在式（6.75）中引入松弛变量y∈RRⁿ，在式（6.76）中引入松弛变量v∈RR^m，得

c+Qx+A^Tλ^T-y=0 （6.81）

Ax-b+v=0 （6.82）

而KKT方程为

Qx+A^Tλ^T-y=-c^T （6.83）

Ax+v=b （6.84）

x≥0 （6.85）

y≥0 （6.86）

v≥0 （6.87）(www.xing528.com)

λ≥0 （6.88）

y^Tx=0 （6.89）

λv=0 （6.90）

现在通过采用受限制的基元规则，隐式地处理互补松弛条件[式（6.89）和式（6.90）]，就可以运用任何线性规划方法来求解这组方程。这里的目标是找到线性规划问题的解，而附加的要求是在每次迭代时满足互补松弛条件。通过对每个方程加入人工变量并使人工变量之和最小化，可以达到目标函数最小化的目的。

例6.6 最小化

f（x）：-10x₁-8x₂+x²₁+2x²₂

约束条件为

x₁+x₂≤10

x₂≤5

x₁≥0，x₂≥0

解6.6 重新将问题表述为

最小化

约束条件为

设人工变量为a₁-a₄，对应的线性规划问题为

最小化a₁+a₂+a₃+a₄

约束条件为

此问题可以通过单纯形法或内点法求解。得到的解为

而对应的费用函数值f（x）=-33。