内点法：通过变换实现可行点向可行域中心移动

求解线性规划问题的另一种方法是内点法（也称为Karmarkar法），其复杂度不管是在平均情况下还是在最坏情况下都是多项式级的。单纯形法存在潜在的最坏情况，其复杂度是指数级的，这种最坏情况发生在到达最优解前经过了可行域的每一个顶点。因此，内点法在过去的几十年中得到了相当的重视。内点法构造一系列严格可行点（即位于多面体的内部而不在其边界上），最终收敛到问题的解。

内点法构造一系列可行点x⁰，x¹，…，它们必须满足Axⁱ=b。因为x⁰满足Ax⁰=b，且下一个点必定满足Ax¹=b，因此两个点之差必然满足AΔx=0。换句话说，每一步都必须在A的零空间中，即A的零空间就是可行域。将-c投影到零空间，就给出了最快变化的方向。然而，如果迭代点x^k很靠近边界（例如图6.3中的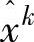），那么改进的量就很小。相反地，如果目前的迭代点很靠近中心（例如图6.3中的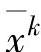），改进的量就很大。内点法的一个关键特性是采用变换的方法使当前的可行点移动到可行域的中心。然后计算新的方向并将内点变换回原始空间。

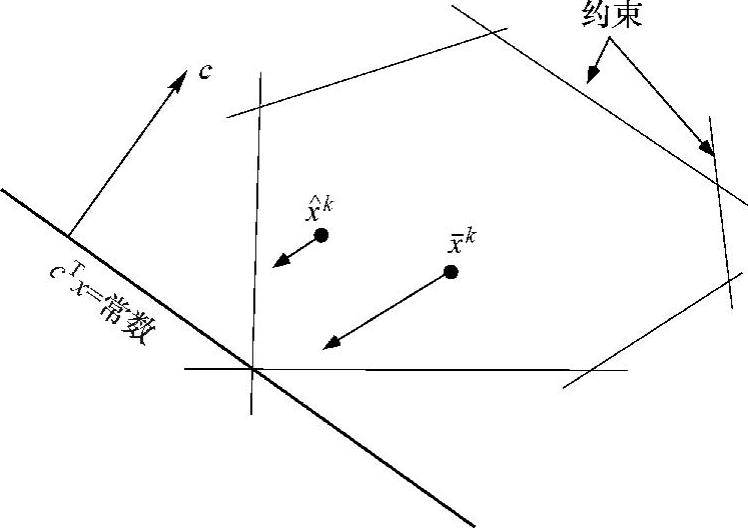
图6.3 可行域内两个不同点的比较

这个变化的方向被称为投影梯度方向，即p^k，而可行点更新为

x^k+1=x^k+αp^k （6.55）式中，α>0是步长。因为可行点必须在A的零空间内，每个p^k必须与A的行正交。投影矩阵P的表达式为

P=I-A^T（AA^T）^-1A （6.56）

投影矩阵P将任意向量v变换为Pv=p，而p将位于A的零空间中，因为AP是零矩阵。

因为将-c投影到零空间给出了最快变化的方向，而为了保证在可行域内，新的迭代必须满足p^k=-Pc。为使迭代点留在可行域的内部，在每步选择步长α时应保证非负约束得到满足。为保证更新后的迭代点留在可行域的内部，选择步长α小于到达边界的全长，通常取0.5≤α≤0.98。

最后要说明的是将迭代点移动到可行域中心的变换。这是通过比例缩放来完成的，其目标是使迭代点在变换后的可行域中离约束边界等距离。因此进行缩放后，x^k=e，其中e=[1 1 … 1]^T。令D=diag（x^k）为对角矩阵，D的对角元素为目前迭代点x^k的元素。这可以通过令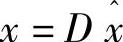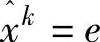，来实现。需求解的新问题变为

最小化

约束条件

式中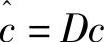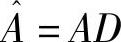，，。缩放后，投影矩阵变为

因此，第k次迭代时，迭代点x^k被缩放为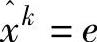，而更新方程变为

随后，将更新后的迭代点重新变换回原始空间

这一过程不断重复直至‖x^k+1-x^k‖<ε。这一过程经常被称为原始仿射内点法^[8]。此方法的步骤可以总结如下：

原始仿射内点法

1.令k=0。

2.令D=diag（x^k）。

3.计算，。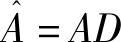

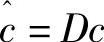4.根据式（6.60）计算。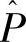

5.令。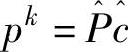

6.令θ=-min_jp_j^k。参数θ用于确定不超出可行域的最大步长。

7.计算。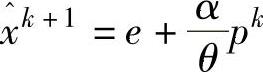

8.计算。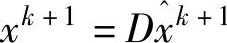

9.若‖x^k+1-x^k‖<ε，则结束计算。否则令k=k+1，返回第2步。

例6.5 用原始仿射内点法重新求解例6.4。

解6.5 为方便起见将问题重新描述如下（包含了松弛变量）：(www.xing528.com)

最小化

f(x):-6x₁-14x₂+OX₃+OX₄+OX₅=z

约束条件为

2x₁+x₂+x₃ =12

2x₁+3x₂ +X₄ =15

x₁+7x₂ +x₅=21

X_l≥0,X₂≥O,X₃≥0,X₄≥O,X₅≥0

一个可行的初始点为

x⁰=[1 1 9 10 13]

而z^O=c^Tc^O=-20。

第1个比例缩放矩阵为

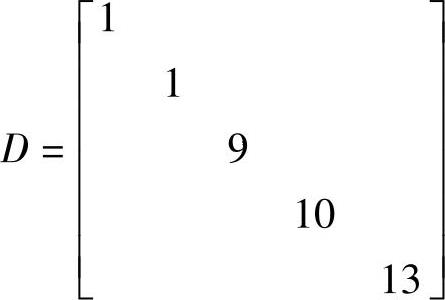
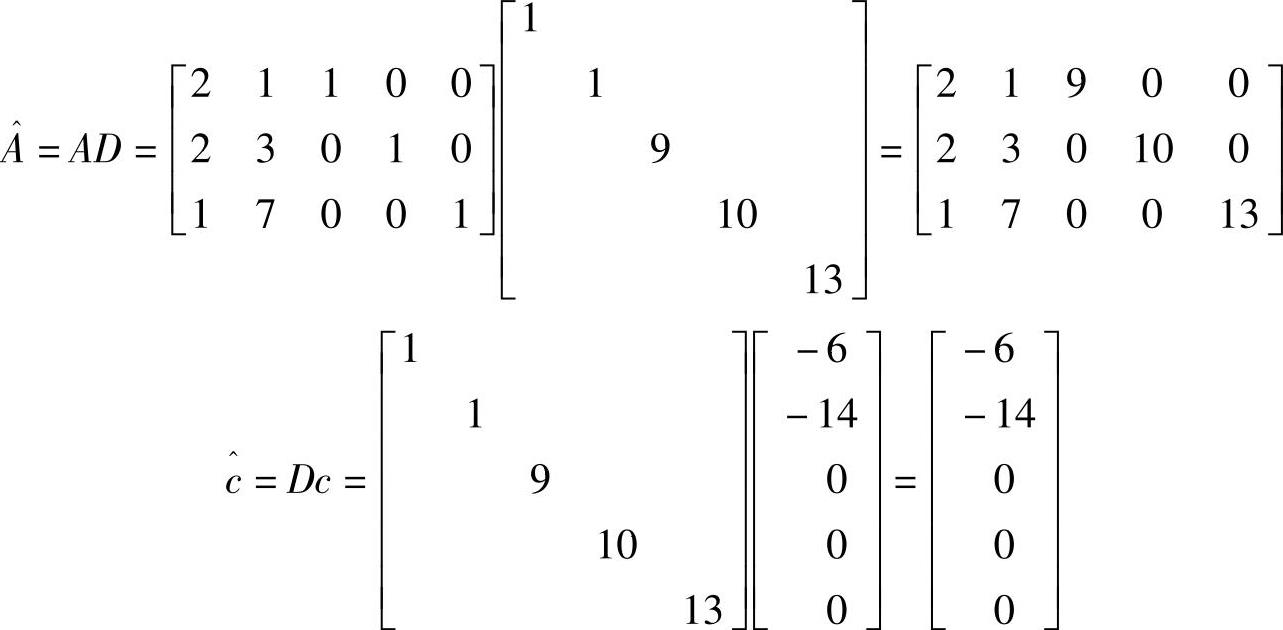
改变比例后的矩阵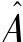和目标函数向量计算如下：

投影矩阵为

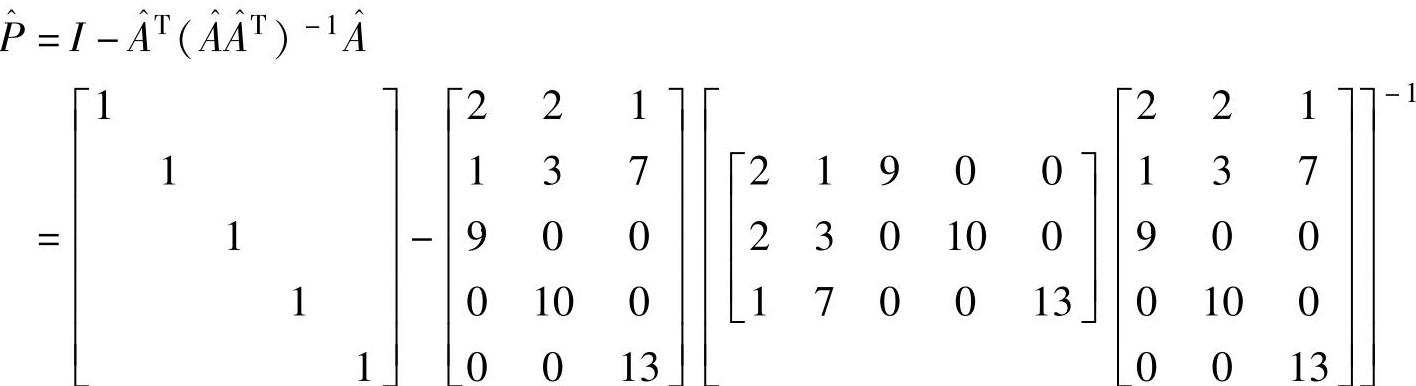
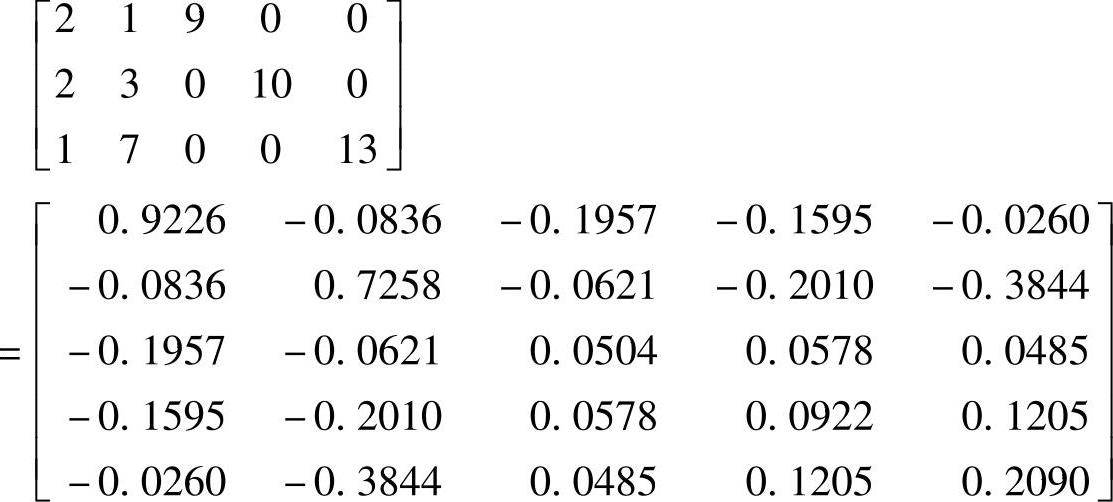
投影梯度为

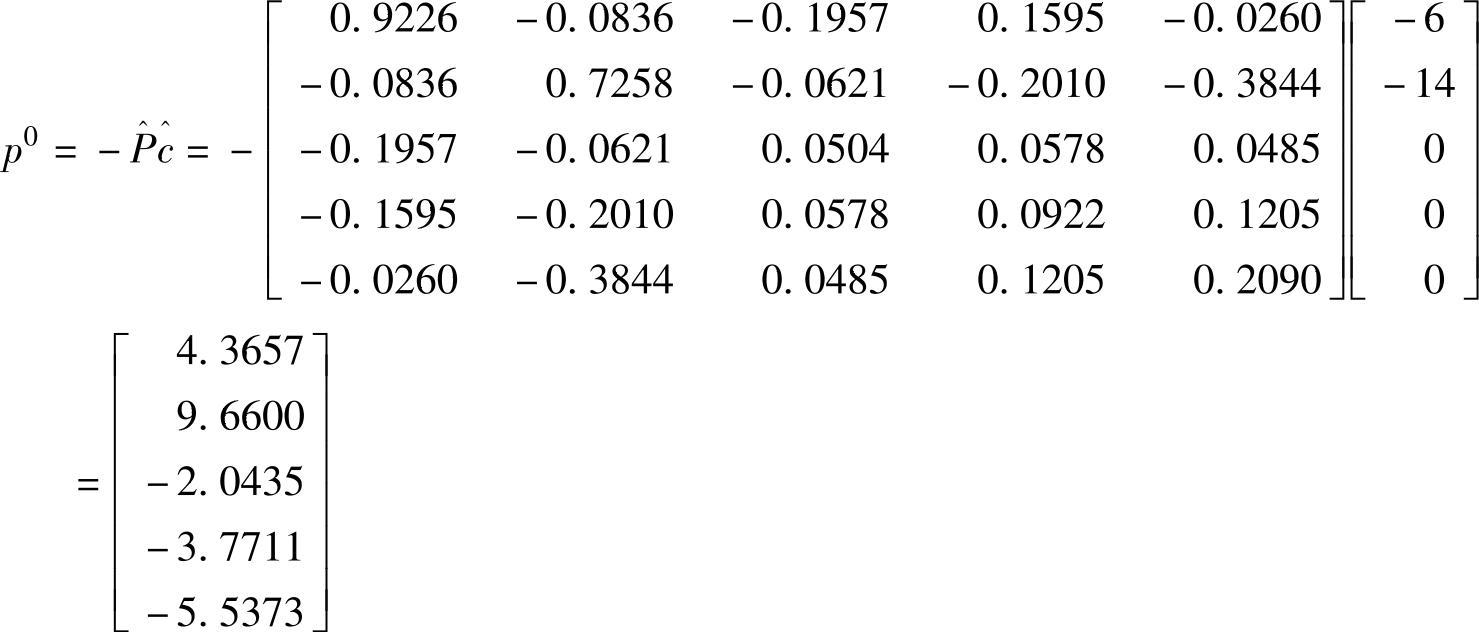
计算θ=-min_jp_j⁰=5.5373。改变比例后的当前迭代点为，用α=0.9在改变比例后的空间中移动到：

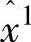将此点变换回原始空间：

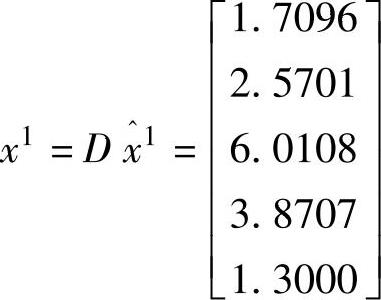
得到更新后的费用函数为c^Tx¹=-46.2383。

再进行一次迭代得到（略去相关说明）

更新后的费用函数是c^Tx¹=-55.8892。

这个过程不断继续直到‖x^k+1-x^k‖<ε，此时问题的解为

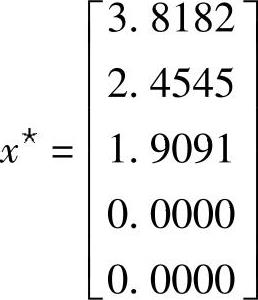
更新后的费用函数是c^Tx^*=-57.2727，两者都与单纯形法的结果一致。