求解线性规划问题的最常用方法之一是著名的单纯形法。单纯形法是一种迭代方法,它将向量x从一个可行基本向量移至另一个,移动方向总是朝着f(x)减小的方向。经过一定步数的迭代后,它能给出精确解,迭代步数通常大大小于组合数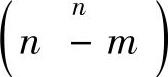 ,一般至多需要2m~3m次迭代(这里m是等式约束的个数)[7]。然而,单纯形法在最坏情况下的复杂度是指数式增长的,这可以通过精心构造的案例展示出来。
,一般至多需要2m~3m次迭代(这里m是等式约束的个数)[7]。然而,单纯形法在最坏情况下的复杂度是指数式增长的,这可以通过精心构造的案例展示出来。
在运用单纯形法的过程中,通常将问题表示成表格的形式,此表格在后续步中按照给定的规则修改。单纯形法的每一步都从一个表格开始。表格的第一行包含有与目标函数f(x)有关的系数。f(x)的当前值显示在表格的右上方。表格中接下来的m行表示等式约束,最后一行包含当前的向量x。表格中与等式约束相关的行可以通过基本行变换进行改变,而不会对解产生影响。
表格必须满足的规则有:
1.向量x必须满足等式约束Ax=b。
2.向量x必须满足不等式x≥0。
3.x中有n个元素是零元(指定为非基变量),剩余的m个元素通常为非零元,并指定为基变量。
4.在定义约束的矩阵中,一个基变量只能出现在一行中。
5.目标函数f(x)只能由非基变量表达。
6.为得到初始解,需在一个或多个约束中加入人工变量。
单纯形算法可以总结如下:
单纯形算法
1.若f(x)的所有系数(即表格的第一行)均大于或等于零,那么当前的向量x即为所求的解。
2.在非基变量中挑选其系数在f(x)中负的最大的,将此变量设置为新的基变量xj。
3.对于每一行i,用新的基变量的系数(aij)去除该行的bi。新的基变量的取值是这些比例中的最小值(例如,第k行的比例最小,则取第k行的比例为xj的值,xj=bk/akj)。
4.使用主元akj通过Gauss消元法将第j列消去。返回步骤1。
式(6.53)中的所有不等式放在一起就形成一个相交的超平面。可行域在这个n维多面体的内部,而f(x)的最小值一定在这个多面体的顶点上。单纯形法通过沿着此多面体最陡峭的边界移动,有规律地搜索这些顶点,直到获得x∗,如图6.2所示。
例6.4 最小化
f(x):-6x1-14x2
约束条件为
2x1+x2≤12
2x1+3x2≤15
x1+7x2≤21
x1≥0,x2≥0
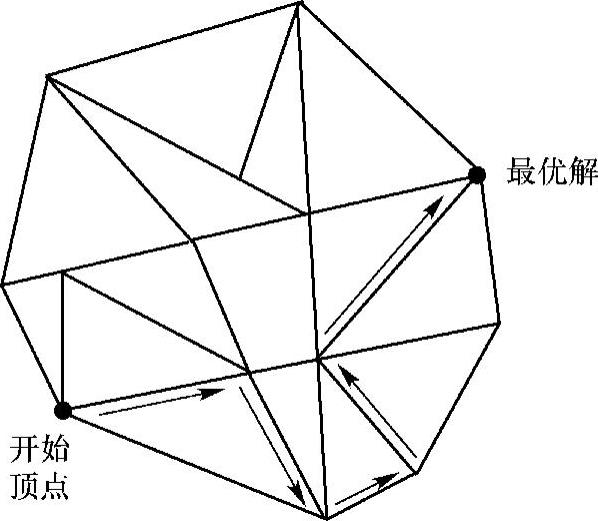
图6.2 单纯形法搜索的例子
解6.4 引入松弛变量x3、x4和x5,使问题变为
最小化
f(x):-6x1-14x2+0x3+0x4+0x5(https://www.xing528.com)
约束条件为
x1≥0,x2≥0,x3≥0,x4≥0,x5≥0
构造求解的表格:

起始向量是x=[0 0 12 15 21]T。f(x)的当前值显示在表格的右上角。下一步,将检查函数f(x)以确定哪个变量会导致f(x)的值有最大的下降。由于-14比-6绝对值大,x2的单位增量引起的f(x)值的下降比x1的单位增量大。因此,保持x1为0不变,而让x2尽可能地增大(即横跨多面体的一条边到下一个顶点)。为了确定x2的新值,考虑如下的约束条件:
0≤x3=12-x2
0≤x4=15-3x2
0≤x5=21-7x2
根据此约束条件,可以得到x2的可能值为x2≤12,x2≤5,x2≤3。最严厉的约束是x2≤3,因此,x2可以增大到3,这样有
x3=12-x2=9
x4=15-3x2=6
x5=21-7x2=0
从而产生一个新的向量x=[0 3 9 6 0]T和f(x)=-42。
新的基变量(非零)是x2、x3和x4,因此f(x)必须用x1和x5来表达。通过变量替换,
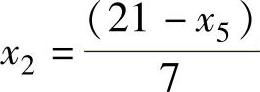
有
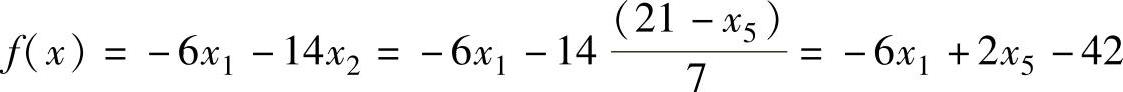
为了满足一个基变量只能出现在一行中的规则,采用Gauss消去法从每一行(有一行除外)中消去x2,采用的主元按前面所述的算法第3步确定。
Gauss消去后的新的表格为
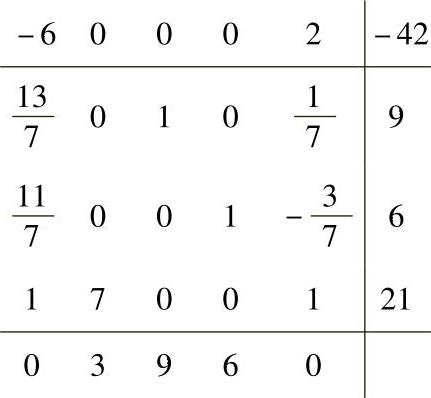
计算步骤重新开始。x5增大时f(x)将会增大,因此,x1被选作基变量。因此,保持x5为0不变,而让x1尽可能地增大。新的约束条件为
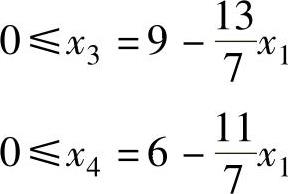
0≤7x2=21-x1
即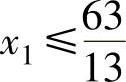 ,
,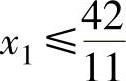 ,x1≤21。严厉的约束是
,x1≤21。严厉的约束是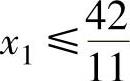 ,因此,设置x1为
,因此,设置x1为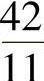 ,然后计算x2、x3和x4的新值。得到新的向量
,然后计算x2、x3和x4的新值。得到新的向量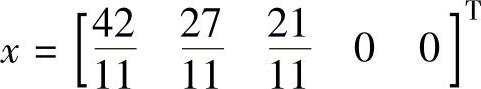 ,而f(x)要用x4和x5来表达:
,而f(x)要用x4和x5来表达:
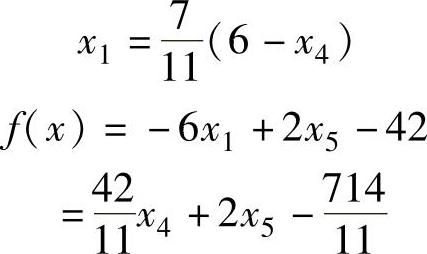
由于f(x)的所有系数都是正的,意味着x4和x5的任何增大都会使f(x)增大,因此单纯形法结束。这表示当前的向量x就是问题的解,且f(x)的最终值是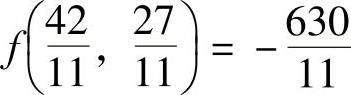 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




