检测坏数据的方法和应用

在一组量测量中经常会包含一个或多个来自于故障仪表或精度很差仪表的量测量。遥测数据会存在由测量和通信引起的误差。这些“坏”数据通常会落在量测量的标准偏差之外，并会影响状态估计过程的可靠性。在严重情况下，坏数据会导致完全不准确的结果。由于“涂污效应”，坏数据会导致估计精度的恶化，因为坏数据会将估计值拖离真值。因此，期望开发一种对数据“好坏”进行度量的方法，从而使状态估计只基于好的数据进行。如果所用的数据导致一个好的状态估计，那么测量值与计算值之间的误差在某种意义上会很小。如果这个误差很大，那么所用数据中必然包含至少一个坏数据。值得采用的一个误差是估计的测量误差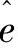，这个误差是真实测量值z与估计测量值之间的差。回顾一下式（6.14）中的误差向量e=z-Ax，因此，估计的测量误差可以表达为

这样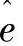，的方差可以表达为

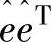的期望值即均值可以表达为

回顾一下E[e·e^T]正是协方差矩阵R=W^-1，且是一个对角矩阵。因此

矩阵

[I-A（A^TWA）^-1A^TW]

具有一个非同寻常的性质，它是一个幂等矩阵。一个幂等矩阵M具有如下性质：M²=M。因此不管M自乘多少次，结果仍然是M。这样，

为了判断估计值与测量值之间是否有显著的差别，一个有用的统计测度是χ²（chi方）不等式检验。这个测度基于χ²概率分布，其形状随自由度k的不同而不同，而自由度k等于量测量的数目与状态量的数目之差。通过比较误差的加权和与特定自由度和显著性水平下的χ²值，可以判定误差是否超过了由随机误差决定的边界。显著性水平表示量测量出现错误的概率值。显著性水平为0.05表示出现坏数据的可能性为5%，或者反过来说是好数据的置信水平为95%。例如，当k=2和显著性水平α=0.05时，如果误差的加权和不超过χ²值5.99，那么就有95%的信心确认此组测量数据是好数据；否则，此组数据中至少含有一个坏数据，不能被采纳。虽然χ²检验用于确定坏数据是否存在是有效的，但它不能对坏数据进行定位。对坏数据进行定位依然是一个需要研究的主题。

用于检测是否存在坏数据的过程如下：

坏数据检测步骤(www.xing528.com)

1.使用z估计x

2.计算误差

e=z-Ax

3.计算误差的平方加权和

4.对k=m-n和设定的概率α，若f<χ²_k，α，则表示数据良好；否则，至少存在一个坏数据。

例6.3 使用χ²不等式检验，设定α=0.01，检查例6.1的测量数据中是否存在坏数据。

解6.3 例6.1中的状态量个数是2，量测量个数是4，因此k=4-2=2。误差平方的加权和为

从χ²值表可以查到，对应本例子的χ²值为9.21。最小二乘平方误差小于χ²值，因此，有99%的置信水平认为量测量是好的。