在很多物理系统中，系统的运行状态不能通过已知方程在已知条件下的解析解直接确定。更普遍的情况是，系统的运行状态是由遍布系统各处的系统状态量的量测量确定的。在很多系统中，量测量的数目多于唯一确定运行点所要求的量测量数目。这种冗余性通常是有意设计的，以抵消测量误差或由仪器故障造成的数据缺失所造成的影响。相反地，并非所有状态量都可以通过量测获得。高温、移动部件或者不适合居住的环境会使得测量某些系统状态量变得困难、危险和昂贵。在这种情况下，缺失的状态量必须通过系统其他的测量信息估计出来。这个过程通常被称为“状态估计”，即从量测量估计未知的状态量。状态估计在测量数据存在不确定性、冗余或相互冲突的条件下给出了系统状态的“最优估计”。好的状态估计会平滑掉测量数据中的随机小误差，检测并识别出大的测量误差，并弥补缺失的测量数据。这个过程试图使系统的真实运行状态（未知）与测量状态之间的误差最小化。
量测量的集合可以用一个向量z来表示，z的组成包含系统状态的量测量（如电压和电流）或系统状态函数的量测量（如潮流）。这样
ztrue=Ax （6.4）
式中，x是系统状态的集合，而A通常不是方阵。误差向量是量测量z和真值之间的差：
e=z-ztrue=z-Ax （6.5）
一般地，为了消除量测量与真值之间误差的符号的影响，通常要求误差的平方取最小值。这样，状态估计器的目标就是寻找误差平方的最小值，即所谓的最小二乘优化法。
误差平方用函数U（x）来表示，有
U（x）=eT·e=（z-Ax）T（z-Ax） （6.7）
=（zT-xTAT）（z-Ax） （6.8）
=zTz-zTAx-xTATz+xTATAx （6.9）
注意，乘积zTAx是一个标量，因此可以改写为
zTAx=（zTAx）T=xTATz
这样，误差平方函数可以表示为
U（x）=zTz-2xTATz+xTATAx （6.10）
误差平方函数的最小值可以通过无约束最优化求得，根据最优化的条件，令该函数关于状态变量x的导数等于零，得到
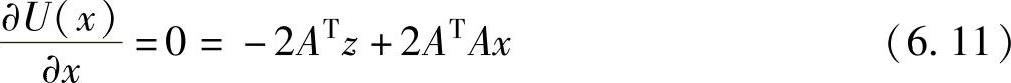
这样有
ATAx=ATz （6.12）
若令b=ATz和
，就有
该方程可以用LU分解法求解。所求得的状态向量x就是当前系统的运行状态（量测量z在此运行状态下测得）的最优估计（误差平方意义上）。测量误差可以表达为
e=zmeas-Ax （6.14）
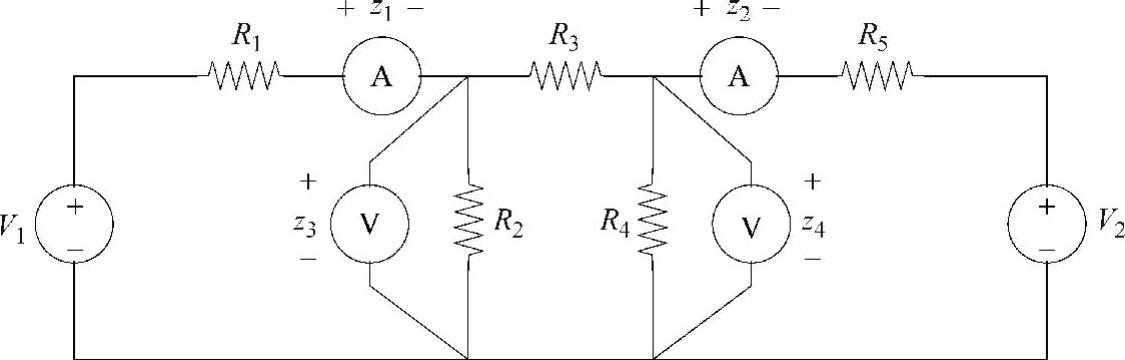
例6.1 如图6.1所示电路的一组量测量如下：
其中，R1=R3=R5=1.5Ω，R2=R4=1.0Ω，求电压源V1和V2的大小。
(www.xing528.com)
图6.1 例6.1的电路图
解6.1 根据Kirchoff电压定律和电流定律，此系统的电压方程和电流方程可以分别写为
-V1+R1z1+z3=0
-V2-R5z2+z4=0
z3/R2-z1+（z3-z4）/R3=0
z4/R4+z2+（z4-z3）/R3=0
上述方程可以写成矩阵形式：
为了得到量测量z和状态量x之间的关系，上述方程必须改写成z=Ax的形式。注意到如果独立考虑A的每一列，上述方程可以很容易用LU分解法求解。这样有
类似地有
从而得到
这样
而
得到
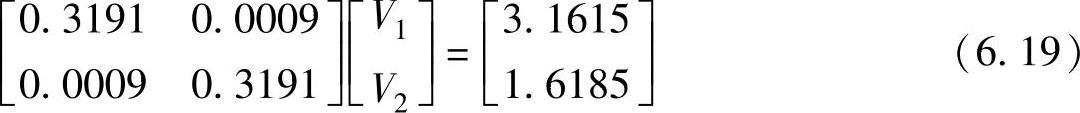
解此方程得到
V1=9.8929
V2=5.0446
此系统量测值与估计值之间的误差为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
