暂态稳定性分析方法解析

同步电机的“经典模型”经常被用来研究电力系统在如下时间段的暂态稳定性，该时间段内，系统的动态主要取决于存储在旋转质量块中的动能。该时间段的长度通常在1～2s。经典模型是在多个简化假设下导出的[1]：

1.机械功率输入P_m，是恒定的。

2.阻尼可忽略。

3.同步电机的暂态电抗后恒定电势模型是有效的。

4.同步电机的转子角与暂态电抗后恒定电势的相位角重合。

5.负荷用恒定阻抗表示。运动方程为

式中，n是电机台数，ω_s是同步角频率，δ_ij=δ_i-δ_j，，而H_i是惯性参数（s）。B_ij和G_ij是归算到电机内部节点的导纳矩阵Y的元素。负荷用恒定阻抗模拟并已归算到导纳矩阵中。经典模型适合于在输电系统故障后的第一摆和第二摆（发电机功角）期间对系统频率响应进行分析。开展暂态稳定性分析的过程如下。

暂态稳定性分析

1.进行潮流计算以获取系统的电压和相角以及有功功率和无功功率。

2.对系统中的每一台发电机i（1，…，n），计算内部电势和初始转子角E∠δ₀：

E∠δ₀=jx′_dI_gen+V_T∠θ_T （5.147）

式中，P_gen+jQ_gen是通过潮流计算获得的有功和无功功率，V_T∠θ_T是发电机的端口电压。

3.对系统中的每个负荷1，…，m，将有功功率和无功功率转换成导纳：

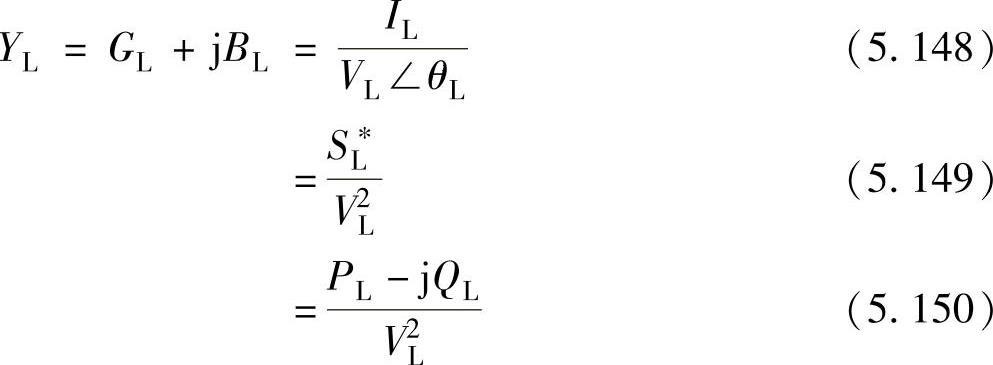
并将并联导纳Y_L加到导纳矩阵相应的对角线上。

4.对系统中的每台发电机，如图5.15所示的那样，增加一条内部母线来增广系统的导纳矩阵，内部母线与发电机端口之间用暂态电抗x′_d来连接。

然后令

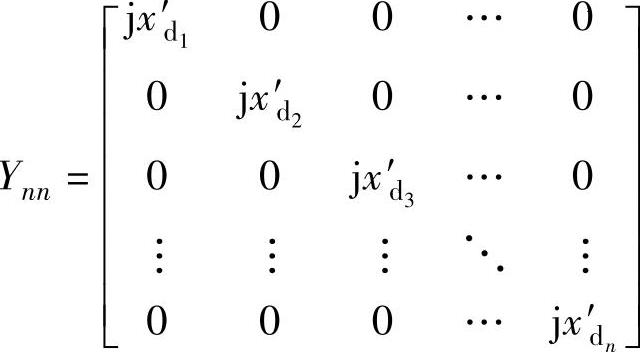
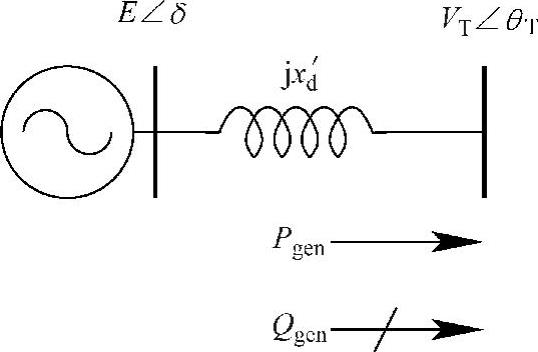
图5.15 暂态电抗后恒定电势模型

以及

Y_nm=[[-Y_nn][0_n×m]]

Y_mn=Y^T_nm

式中，[0_n×m]是一个n×m阶的零矩阵。

之后再令

这个矩阵的结构是建立在如下假设条件上的：发电机母线按照1，…，n编号，而余下的负荷母线按照n+1，…，m编号。

5.只保留发电机内部母线的“降阶导纳矩阵”Y_red由下式给出：

Y_red=[Y_nn-Y_nmY_mm^-1Y_mn] （5.151）

=G_red+jB_red （5.152）

该导纳矩阵是一个n×n阶矩阵，其中n是发电机台数，而原始的导纳矩阵是m×m阶的。

6.重复步骤4和5，以计算故障期间的降阶导纳矩阵以及故障后的降阶导纳矩阵（如果故障前后该矩阵是不同的）。

7.在0<t≤t_apply时间段，采用所选择的数值积分方法基于故障前的降阶导纳矩阵求解暂态稳定性方程式（5.144）和式（5.145），这里t_apply是故障发生的时刻，在很多应用中t_apply是取0。

8.在t_apply<t≤tclear时间段，采用所选择的数值积分方法基于故障中的降阶导纳矩阵求解暂态稳定性方程式（5.144）和式（5.145），这里t_clear是故障被清除的时刻。

9.在t_clear<t≤tmax时间段，采用所选择的数值积分方法基于故障后的降阶导纳矩阵求解暂态稳定性方程式（5.144）和式（5.145），这里t_max是仿真时段的结束点。

仿真结束后，可以画出每台发电机的状态量（δ_i，ω_i）随时间变化的曲线。转子角的响应特性可以用弧度给出，需要的话也可以换算成电角度。转子角频率的单位为rad/s，需要的话也可能换算成Hz（周/s）。对这些波形进行分析就能判断系统的稳定性是否得到了保持。如果系统响应相互之间是逐渐分离的或者呈现出增幅振荡，那么系统很有可能是不稳定的。

例5.9 对如图5.16所示的三机九母线系统，0.1s时在母线8上发生金属性三相短路故障，该故障通过跳开线路8-9来清除。如果故障发生后经过0.12s清除，判断该系统能否保持稳定。

图5.16 例5.9的三机九母线系统

解5.9 根据前述的暂态稳定性分析步骤，第一步是对该系统进行潮流计算。线路和母线数据如图5.16所示。潮流计算结果如下：(www.xing528.com)

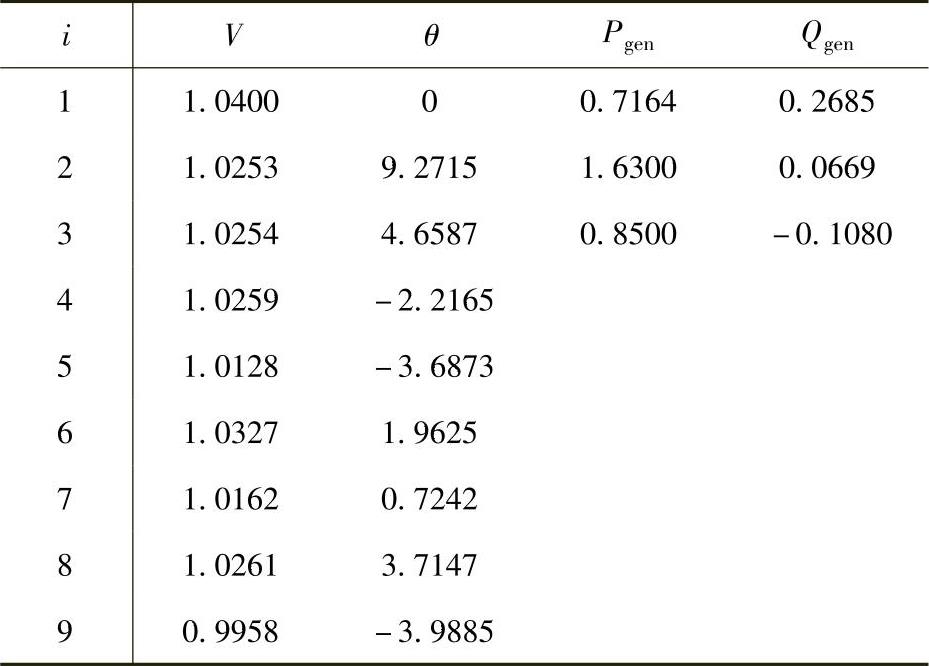
其中母线电压相角的单位是（°），其他数据的单位都是pu。该系统的导纳矩阵如图5.17所示。

图5.17 例5.9的导纳矩阵

该系统的发电机数据为

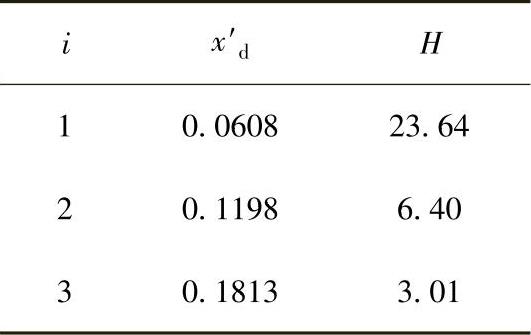
根据潮流计算得到的发电机有功功率、无功功率、电压模值和电压相角，可以计算出每台发电机的内电势和转子角：

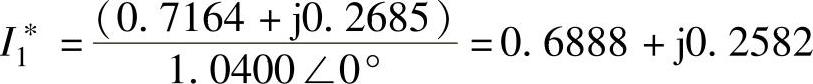
E₁∠δ₁=（j0.0608）（0.6888-j0.2582）+1.0400∠0°=1.0565∠2.2718°

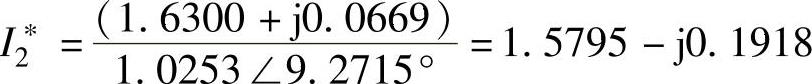
E₂∠δ₂=（j0.1198）（1.5795+j0.1918）+1.0253∠9.2715°=1.0505∠19.7162°

E₃∠δ₃=（j0.1813）（0.8177+j0.1723）+1.0254∠4.6587°=1.0174∠13.1535°

下一步是将负荷转换成等效导纳：

这些导纳被加到原始导纳矩阵的对角线元素上。

现在按照前述的步骤4和步骤5可以计算出降阶的导纳矩阵。故障前的降阶导纳矩阵为

故障中的降阶导纳矩阵可以采用类似的方法得到，但需要改变Y_mm以反映母线8上的故障。三相金属性短路用母线到地短路来模拟，在导纳矩阵中，删除与母线8对应的行与列；因母线8与相邻的母线之间的输电线路现在是直接接地了，因此，它们仍然会在原始导纳矩阵的对角线上出现。Y_nm中对应母线8的列和Y_mn中对应母线8的行必须被删除；而矩阵Y_nn保持不变。故障期间的降阶导纳矩阵为

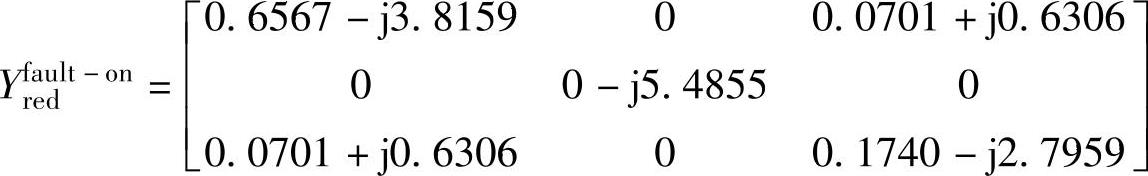
故障后的降阶导纳矩阵也是采用类似方法计算，但需要将线路8-9在矩阵Y_mm中删除。在Y_mm删除线路8-9的操作如下：

Y_mm（8，8）=Y_mm（8，8）+Y_mm（8，9）

Y_mm（8，9）=Y_mm（9，9）+Y_mm（8，9）

Y_mm（8，9）=0

Y_mm（9，8）=0

注意，先要对对角线元素进行更新，然后再对非对角线元素置零。这样可以得到故障后的降阶导纳矩阵为

到此为止，已准备好了不同时间段的降阶导纳矩阵，在合适的仿真时间代入到暂态稳定方程中就可以了。

对暂态稳定方程组采用梯形法进行离散化，可以得到如下的方程组：

式中，

由于暂态稳定方程是非线性的，而梯形法是隐式法，上述方程必须采用Newton-Raphson法在每一个时间点进行迭代求解。迭代方程为

式中，

注意，在求解离散化方程时必须使用LU分解。在每一个时间点必须采用迭代计算直到Newton-Raphson法收敛。故障中和故障后的降阶导纳矩阵应在仿真进行到合适的时间点时代入。转子角和角频率的仿真结果分别如图5.18和图5.19所示。从这些图中的曲线可以看出，系统能够保持稳定，因为在仿真时间段内各曲线没有分离。

图5.18 例5.9中的转子角响应

图5.19 例5.9中的角频率响应