微分代数方程组与受代数流形约束的微分方程组

许多类型的系统可以一般性地描述成如下形式：

F（t，y（t），y′（t））=0 （5.129）

式中，F和y∈R^m。在某些情况下，式（5.129）可以重新写为如下形式：

F（t，x（t），x′（t），y（t））=0 （5.130）

g（t，x（t），y（t））=0 （5.131）

这种形式的方程一般地被称为微分代数方程组（DAE）^[5]。此种形式的DAE也可认为是一组微分方程，即受代数流形[式（5.131）]约束的微分方程组[式（5.130）]。通常，代数方程组式（5.131）是可逆的，即y（t）可以用y（t）=g^-1（t，x（t））来表达，从而式（5.130）可重新写成常微分方程的形式：

F（t，x（t），x′（t），g^-1（t，x（t）））=f（t，x（t），x′（t））=0 （5.132）

尽管常微分方程组（ODE）在概念上是比较容易求解的，但存在多个难以抗拒的原因，要求保留系统方程为原来的DAE形式。因为很多DAE模型是从物理问题导出的，在这些模型中，每个变量都有其各自的特性和物理意义；将DAE转化成ODE会导致方程解的物理信息丢失。此外，求解ODE形式的方程可能计算量更大，因为在转化成ODE时会失去系统固有的稀疏性。而直接求解原始的DAE将得到更多系统行为的信息。

DAE的一种特殊形式是半显式DAE，其形式如下：

0=g（x，y，t） y∈R^m （5.134）

式中，y和g有同样的维度。能写成半显式形式的DAE通常被称为是指标1的微分代数方程组^[5]。求解半显式DAE的最早的成果发表于参考文献[15]，并在参考文献[16]中得到了改进，其做法是将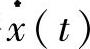用k阶后退差分方程（BDF）来近似替代：

然后求解如下新的方程组以得到近似的x_n、y_n：

ρ_n^xn=h_nf（x_n，y_n，t_n） （5.136）(www.xing528.com)

0=g（x_n，y_n，t_n） （5.137）

将不同的数值积分算法应用于求解微分代数方程，已进行过很多研究。参考文献[44]提出了变步长但固定公式代码的求解方法。特别地，采用经典的四阶Runge-Kutta法来求解x，而用三阶BDF法来求解y。

然而一般情况下，很多DAE可以用任何多步数值积分算法进行求解^[21]，但要求这些多步数值积分算法在求解ODE时是收敛的。将多步数值积分算法应用于求解DAE是直截了当的。通用的多步法公式如式（5.8）所示，将其应用于式（5.133）和式（5.134）得到

0=g（x_n+1，y_n+1，t_n+1） （5.139）

多步法应用于求解半显式的指标1DAE时是稳定和收敛的，其精度与求解同阶非刚性ODE相当^[5]。

对于式（5.138）和式（5.139）的求解，有两种基本方法。一种是迭代法，首先求解式（5.139）得到y_n+1，然后将其代入到式（5.138）求出x_n+1。这个过程在t_n+1处不断重复，直到x_n+1和y_n+1的值收敛，然后再在下一个时间点处进行求解。

另一种方法是同时求解法，即采用诸如Newton-Raphson法等非线性求解器，同时对上述两个方程组进行求解以得到x_n+1和y_n+1。在这种情况下，上述方程组被改写为

0=g（x_n+1，y_n+1，tn+1） （5.141）

Newton-Raphson法的Jacobi矩阵变为

通过求解这个完整的n+m阶方程，就能同时得到x_n+1和y_n+1。

与ODE对于任何初始值都有唯一解不同，DAE不一定有唯一解。DAE的可解性指的是，对于充分不同的输入和相容的初始条件存在一个唯一的解。就DAE来说，对于非状态变量（代数变量）只存在一组初始条件。与系统输入相容的初始条件被称为容许初始条件，容许初始条件满足如下方程：

y₀=g^-1（x₀，t₀） （5.143）