如何选择合适的积分步长来求解微分方程？

为了提高计算效率，在满足预设精度的条件下，希望选择尽可能大的积分步长。如果所选的数值积分算法是数值稳定的，那么通过时刻关注该算法的局部截断误差就能保证精度水平。当函数x（t）快速变化时，步长就应该选得足够小，以能捕捉到函数的主导性动态特征。相反地，当函数x（t）在一个有限时间段内变化不大（接近线性）时，步长就可以选得较大，且仍然能保持精度水平。对数值积分算法真正构成挑战的是，x（t）的动态响应既包含了快速变化的时间段，也包含了慢速变化的时间段。在这种情况下，期望在整个仿真时间段内积分步长可以伸缩，实现上述目标的途径是基于局部截断误差边界来确定积分步长。

考察梯形法的绝对局部截断误差：

该局部截断误差依赖于积分步长h和函数x（t）的三阶导数x^（3）（τ）。如果选择局部截断误差在如下范围内：

B_L≤ε≤B_U （5.112）

式中，B_L和B_U分别表示预先设定的上边界和下边界。那么积分步长的范围就是

如果x（t）是快速变化的，那么x^（3）（τ）将会变大，这时h就要选小以满足ε≤

B_U；而如果x（t）变化不快，那么x^（3）（τ）就会变小，从而选择比较大的步长h也能满足ε≤B_U。因此可以导出如下的计算积分步长的步骤。

积分步长选择算法：

先尝试用一个积分步长h_n+1来从x_n，x_n-1，…计算x_n+1。

1.用x_n+1计算出局部截断误差ε_T。

2.假如B_L≤ε_T≤B_U，那么说明步长h_n+1是可以的，令h_next=h_n+1，然后继续。

3.假如ε>B_U，说明h_n+1太大，那么令h_n+1=αh_n+1，返回第1步，重复以上操作。

4.假如ε≤B_U，那么通过，h_n+1可行，令h_next=αh_n+1，然后继续。其中(www.xing528.com)

式中，B_L≤B_avg≤B_U，k是算法的阶数。

一些微分方程求解的商业软件包对积分步长的选择与上述方法稍有不同。在这些软件包中，如果局部截断误差小于下边界B_L，则尝试的积分步长也失败，并重新尝试一个更大的积分步长。同样地，这里也存在一个折中问题，一方面采用较大的时间步长重新计算x_n+1需要花费计算量，但计算步长大了；而另一方面直接采用已经得到的结果，没有新增计算量，但计算步长小。

实现上述确定计算步长算法的难度在于需要计算x（t）的高阶导数。因为x（t）的解析式是不知道的，其高阶导数必须通过数值计算来求得。一种常用的方法是用差分方法来近似求导计算。x（τ）的第（k+1）阶导数可以近似为

x^（k+1）（τ）≈（k+1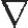）！_k+1x_n+1 （5.115）

式中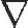，_k+1x_n+1的计算是递归的：

例5.8 推导梯形法的积分步长选择公式，假定局部截断误差的上边界为10^-3。

解5.8 梯形法的局部截断误差表达式为

第一步我们先求出三阶导数的表达式：

x^（3）（τ）≈3！₃x_n+1 （5.124）

将B_U和三阶导数的近似式代入式（5.123）中，得到h的取值范围为

式中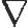，₃x_n+1在式（5.127）中给出。