如何正确求解刚性系统：Adams-Bashforth法

Gear法最初是用来求解刚性常微分方程组的。所谓刚性系统指的是同时具有“非常快”与“非常慢”时间动态的宽时间范围动态系统。线性刚性系统的特征值大小常常会跨越好几个数量级。对于非线性系统，若与待研究工作点相对应的Jacobi矩阵具有大范围分散的特征值，那么该非线性系统就是刚性系统。为了高效并精确地求解刚性微分方程，期望所采用的多步算法是“刚性稳定”的。合适的数值积分算法应能允许步长在一个较宽的范围内变化而仍然保持数值稳定。一个刚性稳定算法具有如图5.10所示的三个稳定域：

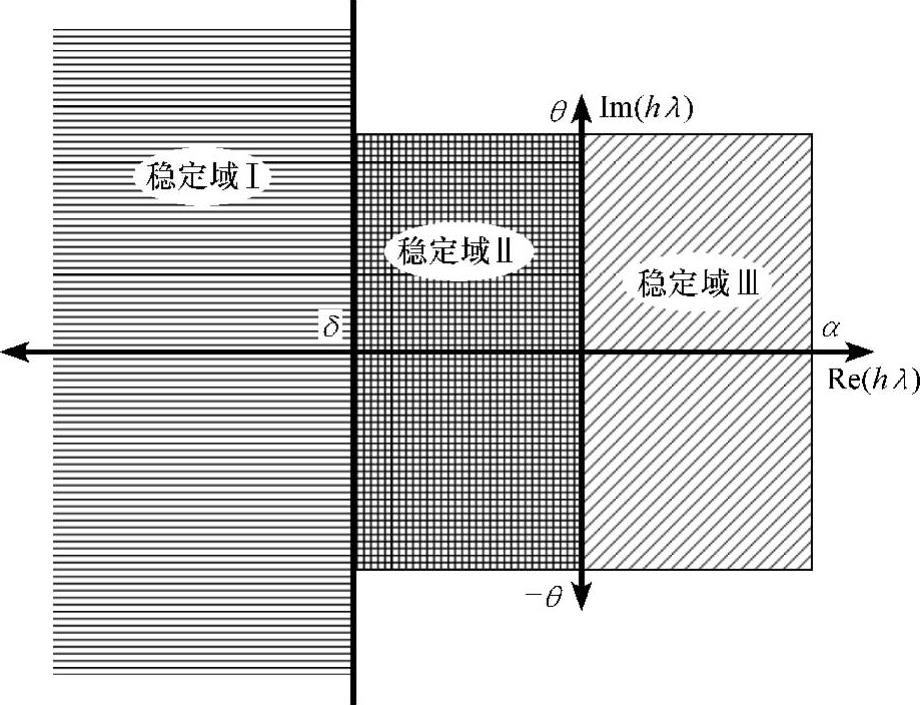
图5.10 刚性稳定所要求的稳定域

1.区域Ⅰ是绝对稳定域

2.区域Ⅱ是精确与稳定域

3.区域Ⅲ是精确与相对稳定域

大模值负特征值仅仅在常微分方程解的初始阶段会对解有显著的影响，然而，在整个求解过程中，必须考虑它的作用。大模值负特征值（λ<0）将会在1/|λ|时间内按1/e的速率迅速衰减。如果hλ=γ+jβ，那么每一步中幅值的变化均为e^γ。如果γ≤δ≤0，这里δ为区域Ⅰ与区域Ⅱ的分隔线所对应的实部值，那么在每一步中该分量都会至少减少e^δ。在有限步之后，快变分量的影响可以忽略不计，且它们的数值精度也不再重要。因此要求数值积分算法在区域Ⅰ中保证绝对稳定。

在原点附近，数值精度变得更加重要，同时也需要保证算法相对或绝对稳定。所谓的相对稳定域，指的是这样一个域，满足式（5.97）的特征多项式的外部特征值小于主特征值的所有hλ的值。所谓主特征值指的是能够最准确地确定系统响应的特征值。如果算法在区域Ⅲ中是相对稳定的，那么在这一区域中系统的响应将由主特征值主导。如果γ>α>0，系统响应中有一个分量每一步将至少会增加e^α。必须选择足够小的步长来限制这一增量，从而能够追踪数值的变化。

如果‖β‖>θ，每一步中至少存在θ/2π个完整的振荡周期。除了响应迅速衰减的区域Ⅰ与没有用到γ>α条件的区域，其余区域中必须捕捉到振荡响应。实际上，为了精确地捕捉到振荡的幅值与频率，惯用的做法是每个振荡周期具有8个或更多个时间节点；因此，在区域Ⅱ中，θ的边界选取为π/4。

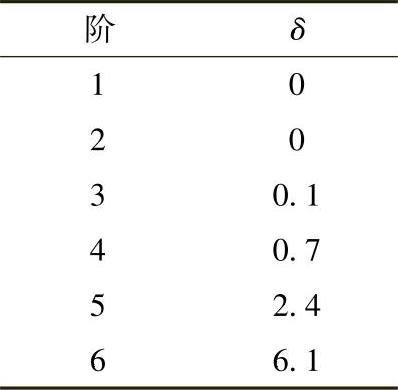
检查Adams-Bashforth类算法表明，它们不满足刚性稳定的准则，因此并不适合用于求解刚性系统。只有一阶和二阶Adams-Moulton算法（分别为后退Euler法和梯形法）满足刚性稳定的准则。另一方面，Gear法是专门开发出来用于求解刚性系统的^[14]。直到六阶的Gear法都满足刚性条件且具有如下的δ值^[6]：

例5.7 采用三阶Adams-Bashforth、Adams-Moulton与Gear法求解如下系统，并进行比较。

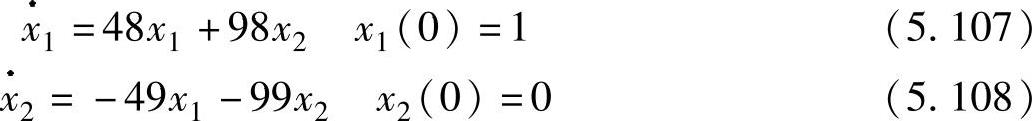
解5.7 例5.7的精确解为

x₁（t）=2e^-t-e^-50t （5.109）(www.xing528.com)

x₂（t）=-e^-t+e^-50t （5.110）

该精确解如图5.11所示。两个状态量都包含了快变分量与慢变分量，其中快变分量主导了初始响应，而慢变分量主导了长期的动态响应。由于Gear法、Adams-Bashforth法与Adams-Moulton法是多步法，因此采用绝对稳定的梯形法来进行初始化，前两步或前三步采用梯形法和较小的步长。

步长为0.0111s的Adams-Bashforth法结果如图5.12所示。注意，即使步长小到0.0111s，该算法的固有误差也最终导致系统的响应呈现出数值不稳定性。可以通过减小步长来增加系统的数值稳定性，但在积分区间（t∈[0，2]）内就需要更多的计算步数，从而使计算效率低下。

采用步长为0.15s的Adams-Moulton法求解此刚性系统，结果如图5.13所示。尽管与Adams-Bashforth法相比，Adams-Moulton法可以使用大得多的积分步长，但Adams-Moulton法并不具有数值的绝对稳定性。当积分步长h=0.15s时，Adams-Moulton法已呈现出数值不稳定性。注意，采用Adams-Moulton法所得出的结果是在精确解附近随时间增幅振荡的。

采用步长为0.15s的Gear法求解此刚性系统，结果如图5.14所示，注意，所采用的步长与图5.13所示的Adams-Moulton法相同。Gear法是数值稳定的，其全局误差随着时间的增长而减小。

比较三种积分算法的结果，说明采用专门开发的积分算法来处理刚性系统是必要的。尽管三阶Adams-Bashforth法与Adams-Moulton法具有绝对稳定的区域，但这些区域不足以确保对刚性系统进行精确的求解。

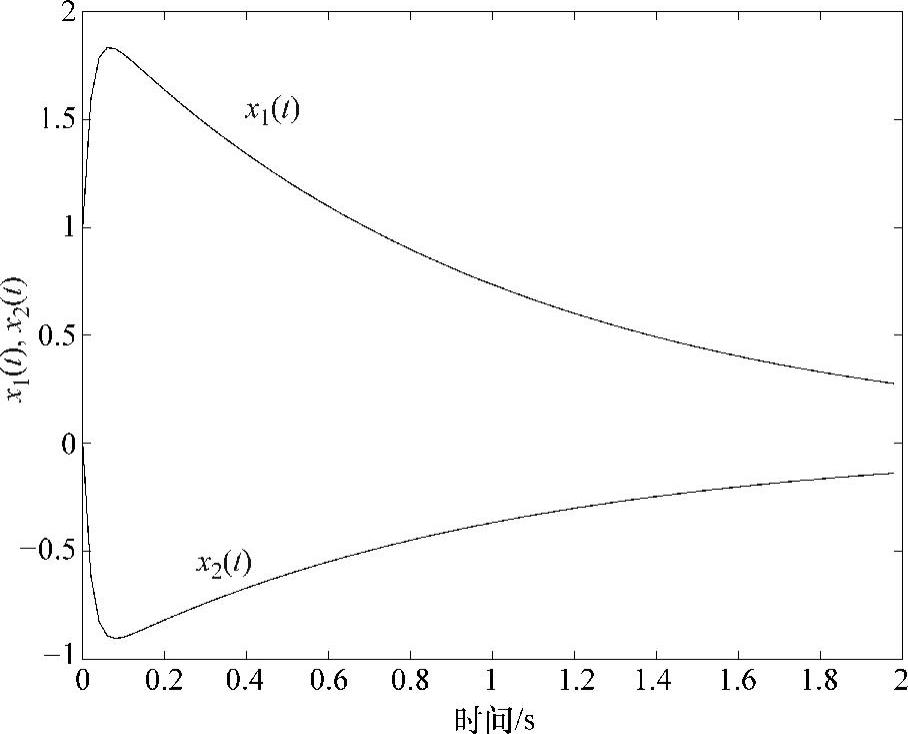
图5.11 刚性系统的响应

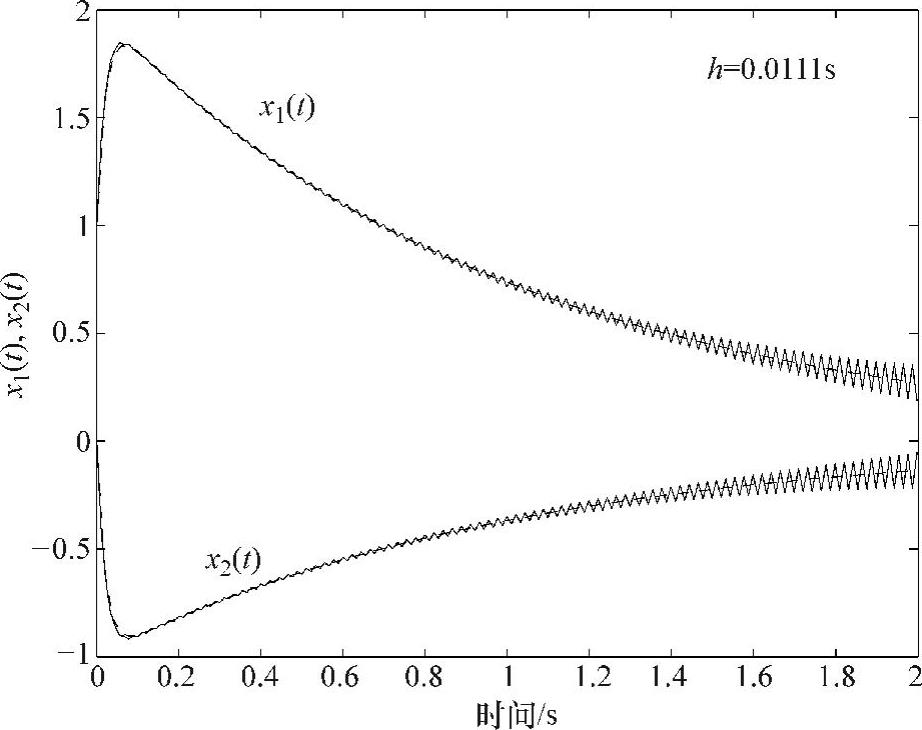
图5.12 步长为0.0111s时Adams-Bashforth法求解刚性系统的结果

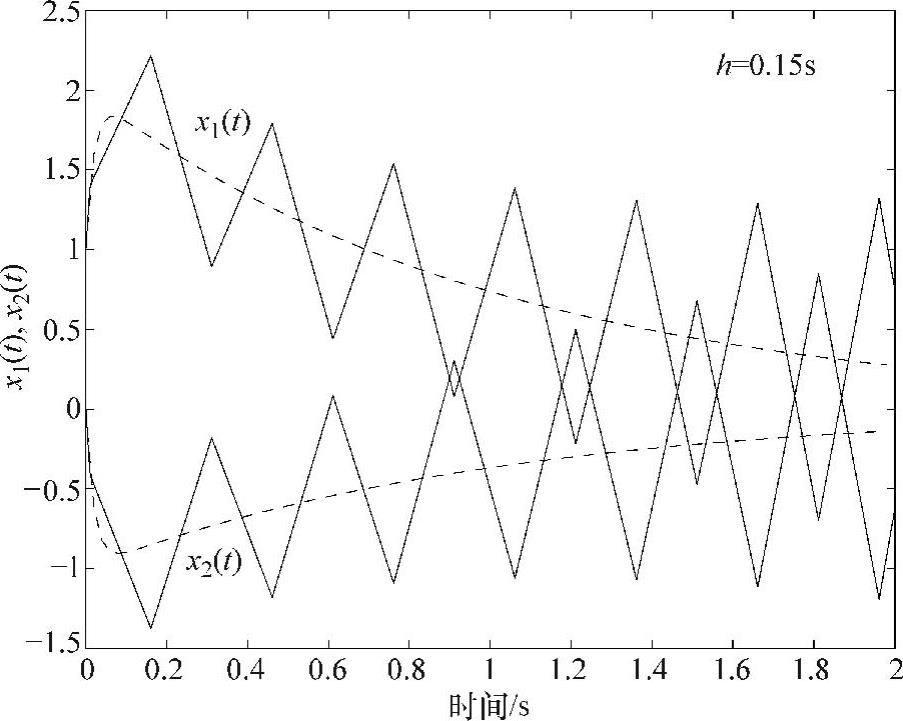
图5.13 步长为0.15s时Adams-Moulton法求解刚性系统的结果

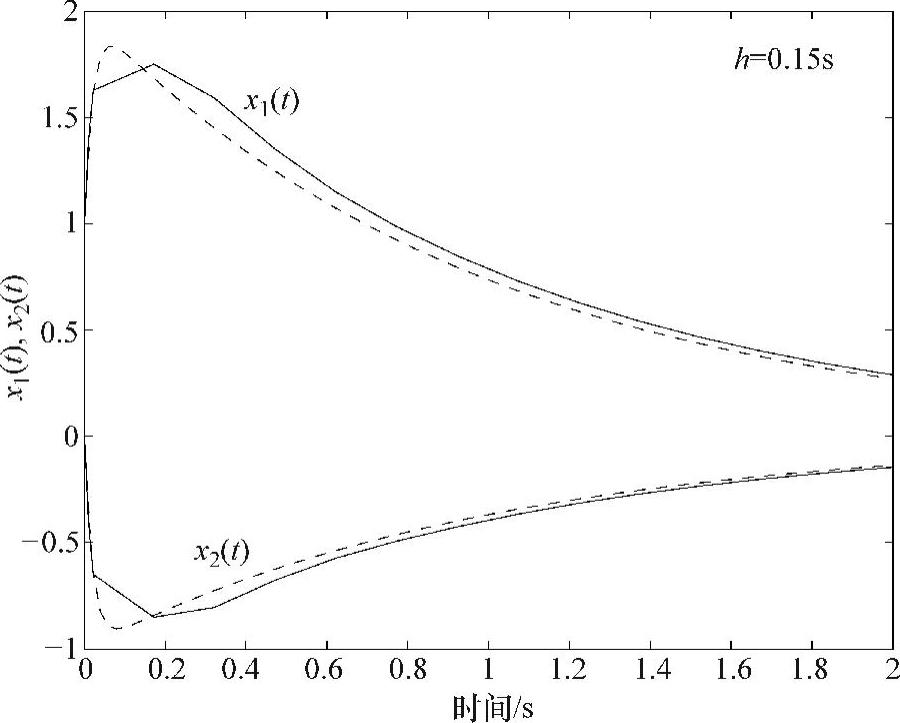
图5.14 步长为0.15s时Gear法求解刚性系统的结果