数值稳定性分析及其在数值积分算法中的重要性

从前面的讨论中可以发现，积分步长的选择直接影响算法的精度；但积分步长的选择对数值稳定性的影响还没有给出明确的结果。数值稳定性保证了算法的全局截断误差保持在边界之内；也就是说，数值稳定性保证了每一步计算产生的误差不会随着时间的增长而累积起来，即每一步的误差随着时间的增长是衰减的。这样，对于数值稳定的算法，在积分步长选择时只需要考虑局部截断误差就可以了。为了分析步长对算法数值稳定性的影响，考察如下简单的标量微分方程：

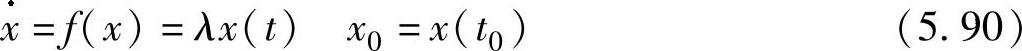
通过观察，可以得到上述方程的解为

x（t）=x₀e^（λt） （5.91）

若λ<0，当t→∞，x（t）→0；相反，若λ>0，当t→∞，x（t）→∞。数值稳定性保证了计算过程的全局行为与实际系统的真实行为相匹配。考察将向前Euler法应用于式（5.90）所示的标量系统：

x_n+1=x_n+hλx_n

=（1+hλ）x_n

故有

x₁=（1+hλ）x₀

x₂=（1+hλ）x₁=（1+hλ）²x₀

︙

x_n=（1+hλ）ⁿx₀

若λ<0，应有t→∞时，x（t）→0；对照上述求解过程，应满足如下条件：

|1+hλ|<1 （5.92）

因此，对于λ<0的系统，要使求解过程数值稳定，hλ的值必须落在以（-1，0）为圆心的单位圆内，如图5.5所示。故λ的绝对值越大，积分步长h就越小。

同样地，考察将后退Euler法应用于同一个标量系统：

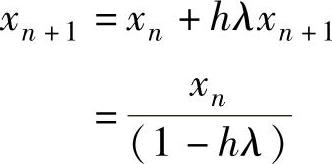
故有

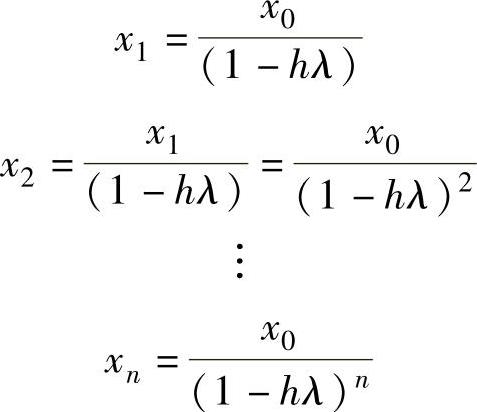
若λ<0，应有t→∞时，x（t）→0；对照上述求解过程，应满足如下条件：

|1-hλ|>1 （5.93）

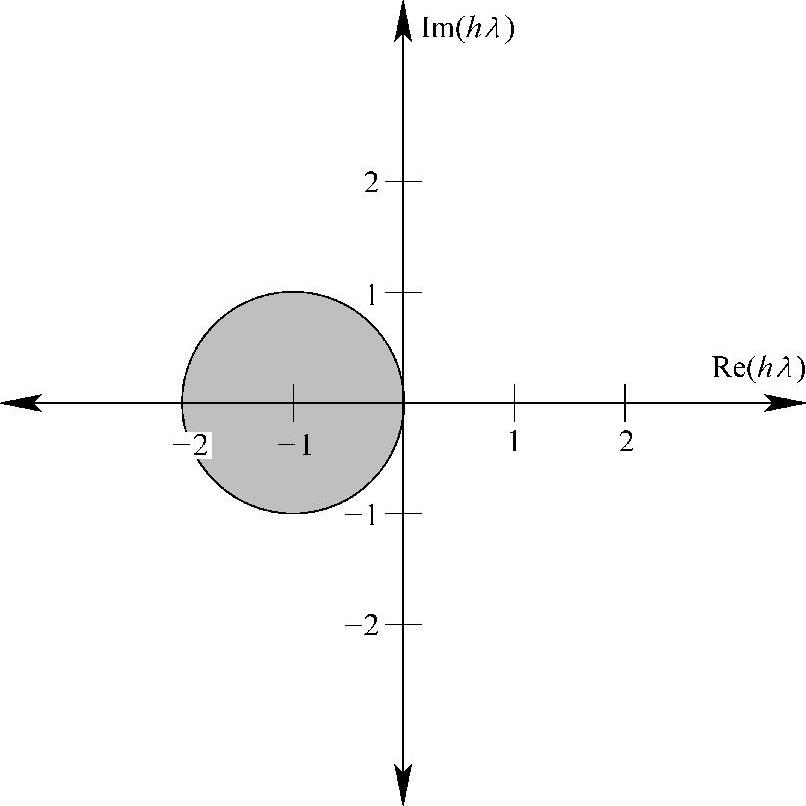
图5.5 向前Euler法的绝对稳定域

因此，对于λ<0的系统，要使求解过程数值稳定，hλ的值必须落在以（1，0）为圆心的单位圆之外的区域中，如图5.6所示。这意味着对于所有的λ<0，后退Euler法都是数值稳定的。因此，如果实际系统是稳定的（即满足λ<0），那么积分步长可以取任意大，而不会影响算法的数值稳定性。这样，积分步长的选择就只依赖于局部截断误差。注意，如果hλ的值很大，x_n将快速趋向零。这个特性本身显示了后退Euler法具有过阻尼的倾向，这在图5.1中已能够看到。

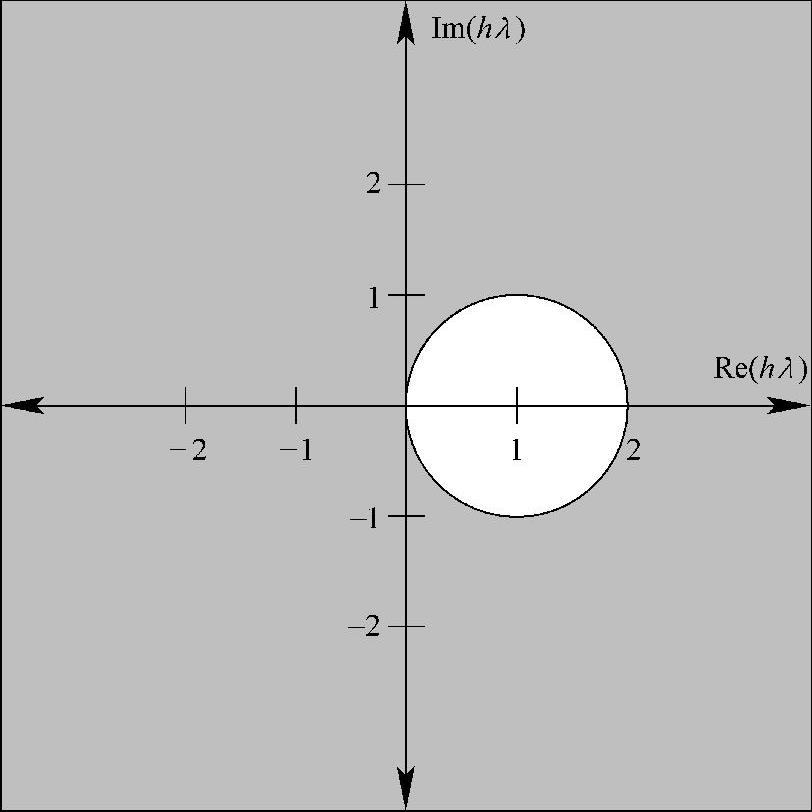
图5.6 后退Euler法的绝对稳定域

将上述分析方法应用于一般形式的多步法，得到

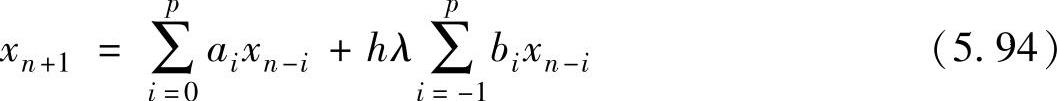
重新排列多步法的各项，得到

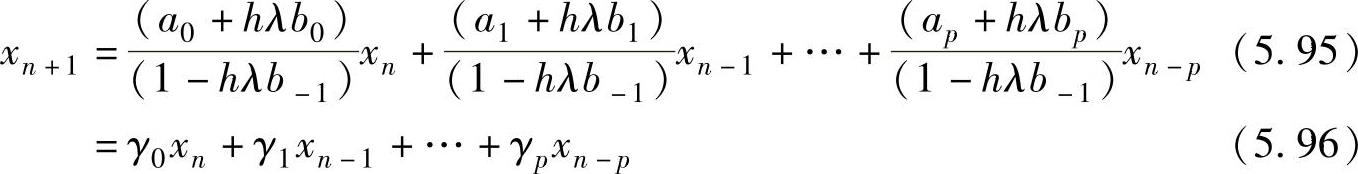
上述关系确定的特征方程为

P（z，hλ）=z^p+1+γ₀z^p+…+γ_p=0 （5.97）

式中，z¹，z²，…，z^p+1为式（5.97）的（复）根，故有

若λ<0，要使得n→∞，x_n+1→0，必须对所有的j=1，2，…，p+1有z_j<1。因此，只有当给定的hλ能使特征方程P（z，hλ）=0的根均满足|z_i|<1（i=1，…，k）时，多步法才是绝对稳定的。绝对稳定性意味着全局误差将随着n的增大而减小。在hλ复平面上，能使特征方程P（z，hλ）=0的根均满足z_i<1（i=1，…，k）的区域被定义为绝对稳定域。令

P（z，hλ）=P_a（z）-hλP_b（z）=0

式中，(www.xing528.com)

P_a（z）≜z^p+1-a₀z^p-a₁z^p-1-…-a_p

P_b（z）≜b_-1z^p+1+b₀z^p+b₁z^p-1+…+b_p

这样

由于z为复数，它也可以被表示为以下形式

z=e^（jθ）

该区域的边界可以通过在复平面上画出hλ的轨迹得到（令θ在[0，2π]范围内改变），其中

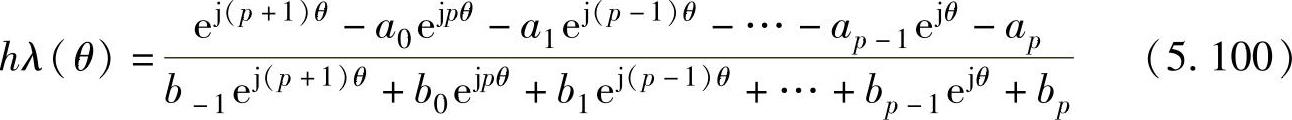
例5.6 画出三阶Gear法和三阶Adams法（包括隐式法和显式法）的绝对稳定域。

解5.6

（1）Gear法

令p=k-1和b₀，b₁，…=0，在hλ复平面上根据式（5.100）画出hλ的轨迹（令θ在[0，2π]范围内改变），可以得到Gear法的绝对稳定域

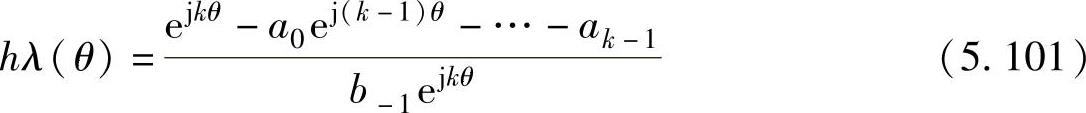
代入三阶Gear法的各系数的值，得到

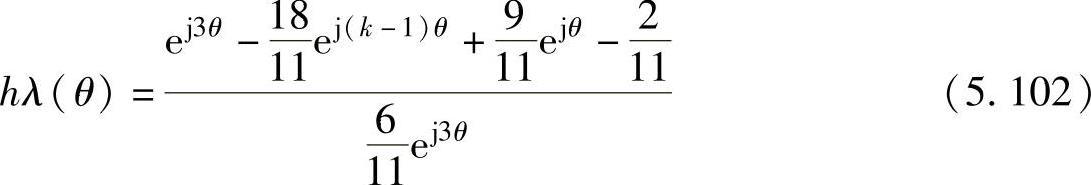
令θ在[0，2π]范围内改变，可以画出三阶Gear法的绝对稳定域，如图5.7中阴影区域所示。

（2）Adams-Moulton法（隐式法）

令p=k-1和a₁，a₂，…=0，在hλ复平面上根据式（5.100）画出hλ的轨迹（令θ在[0，2π]范围内改变），可以得到Adams-Moulton法的绝对稳定域：

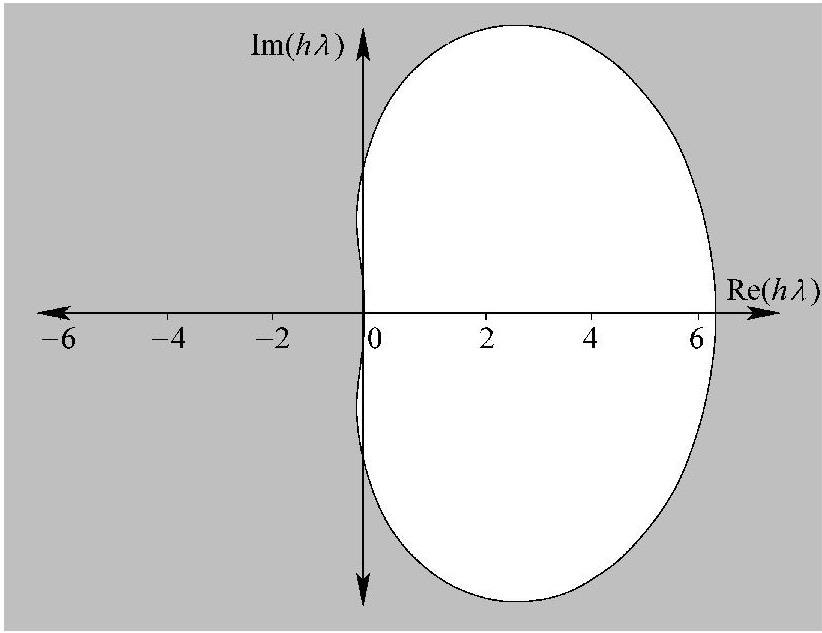
图5.7 三阶Gear法的绝对稳定域

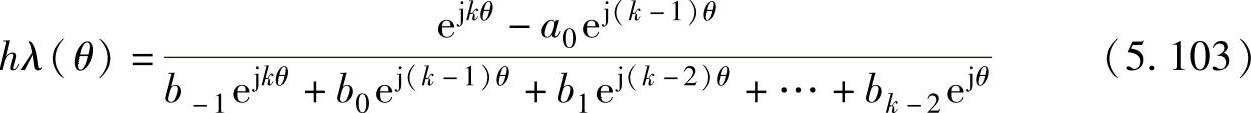
代入三阶Adams-Moulton法各系数的值，得到

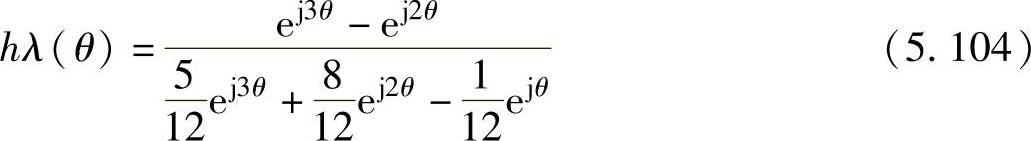
三阶Adams-Moulton法的绝对稳定域如图5.8的阴影部分所示。

（3）Adams-Bashforth法（显式法）

令p=k-1，b_-1=0和a₁，a₂，…=0，在hλ复平面上根据式（5.100）画出hλ的轨迹（令θ在[0，2π]范围内改变），可以得到Adams-Bashforth法的绝对稳定域：

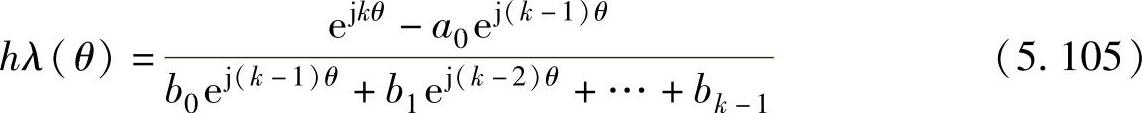
代入三阶Adams-Bashforth法各系数的值，得到

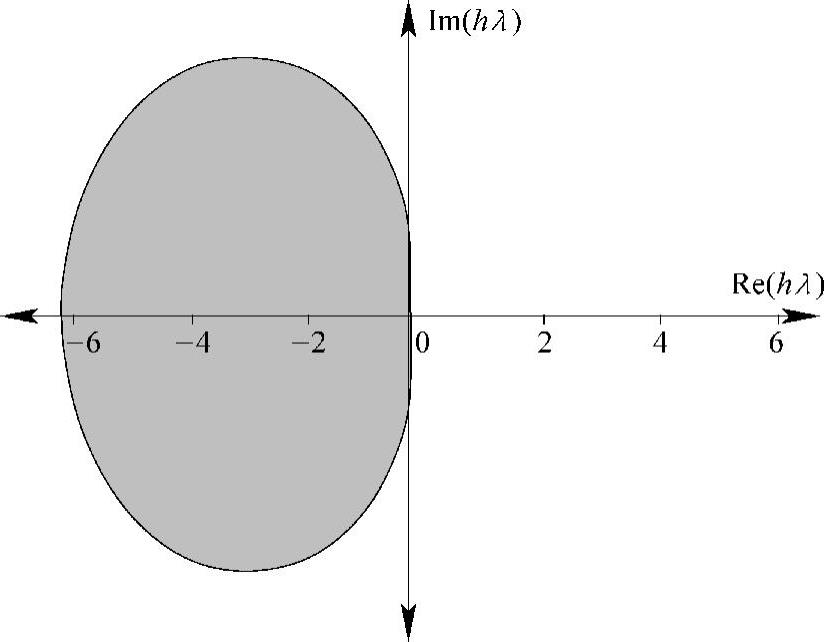
图5.8 三阶Adams-Moulton法的绝对稳定域

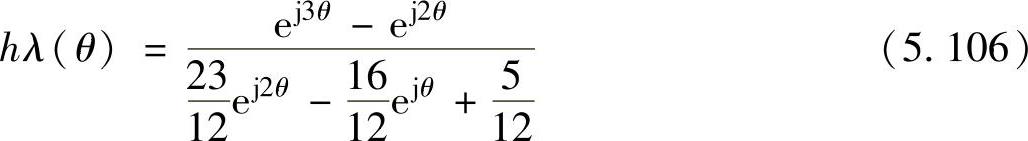
三阶Adams-Bashforth法的绝对稳定域如图5.9的阴影部分所示。

这个例子说明了隐式法和显式法的一个主要区别。在阶数相同的情况下，两种隐式法（Gear法和Adams-Moulton法）的绝对稳定域都比显式法（Adams-Bashforth法）大得多。Gear法的绝对稳定域几乎包含了hλ复平面的左半平面；因此，对于任意一个稳定的动态系统，其积分步长可以取得任意大而不需要考虑步长对数值稳定性的影响。Adams-Moulton法的绝对稳定域也比Adams-Bashforth法大得多。一般地，显式法的稳定域比同阶的隐式法的绝对稳定域小得多。因此，隐式法常被应用于商业化的微分方程求解算法包中，而且积分步长完全根据局部截断误差准则来选择。随着算法阶数的增加，绝对稳定域将缩小，但精度将提高。因此数值积分算法需要折中考虑精度、稳定性和数值计算效率三者的关系。

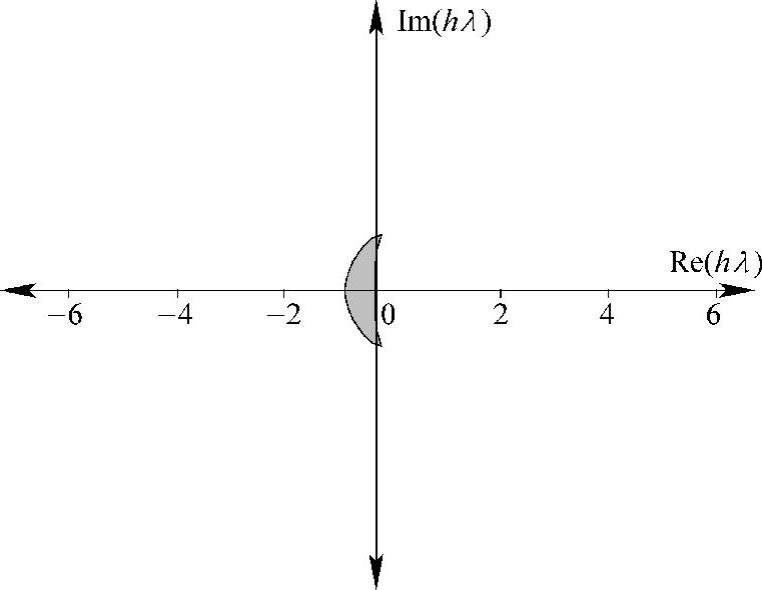
图5.9 三阶Adams-Bashforth法的绝对稳定域